回字有四样写法,你知道么?
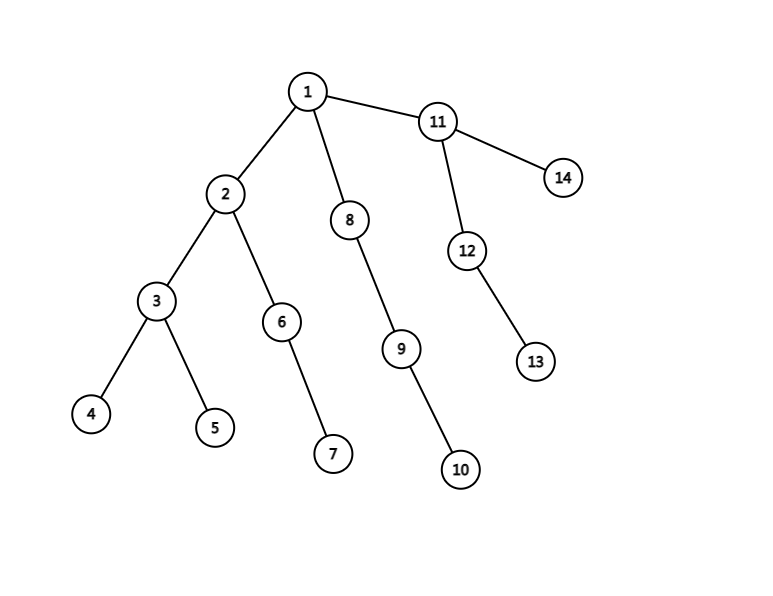
lca,即最近公共祖先,如上图中 2 和 13 的 lca 是 1,5 和 6 的 lca 是 2。
众所周知,LCA 的主流求法有 4 种。
那么,你都会了吗?
树链剖分
由于重儿子优先搜索,同一条重链上的点的时间戳也是连续的(如图上的 1,2,3,4,8,9,10 等)。
那么树剖求 lca 的过程是:
选择两点中 top(重链顶点)深度较大的一个,跳到 top 的 fa 节点,直到两点的 top 相同(即处在同一条重链),此时深度较小的即为两点的 lca。
至于为什么要选择跳节点的 top 深度较大的而不是节点深度较大的。
比如下图以 1 为根的树(随手画的,图丑勿喷):
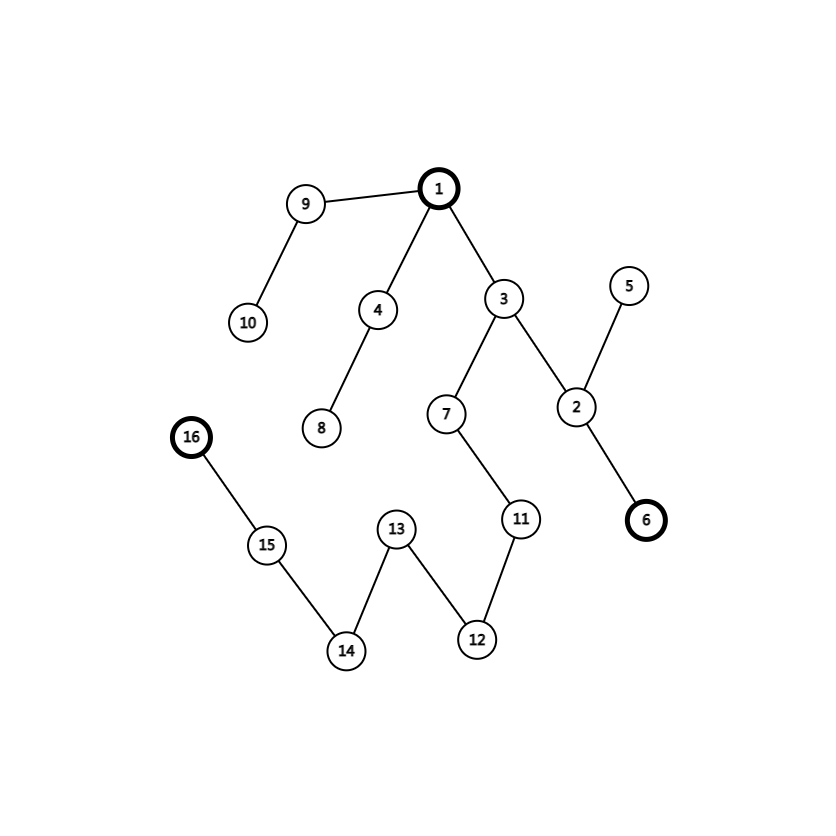
剖完之后是这样:
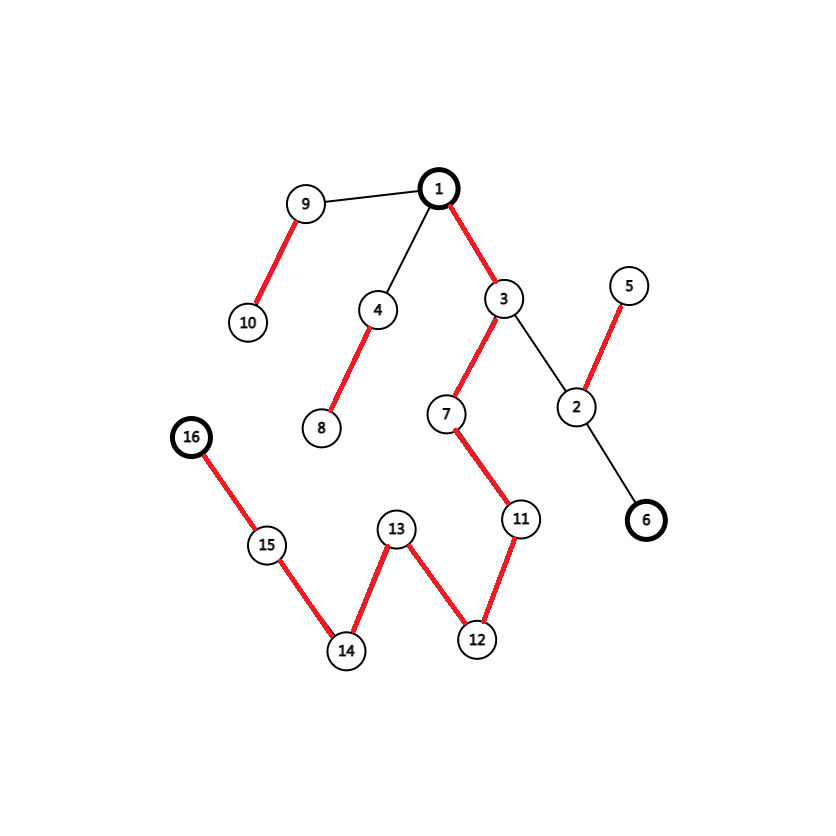
假设求 6 和 16 的 lca。
那么显然,top[6]=6,top[16]=1,而且 dep[16]>dep[6],dep[1]<dep[6],如果跳 16 的 top,那么求得的 lca 绝对不会是正确的。
const int inf=5e5+7;
int n,m,s;
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf],son[inf],siz[inf],dep[inf];
void dfs1(int now,int from)
{
dep[now]=dep[from]+1;
fa[now]=from;siz[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs1(p,now);
siz[now]+=siz[p];
if(siz[son[now]]<siz[p])
son[now]=p;
}
}
int top[inf],dfn[inf],rnk[inf],dfns;
void dfs2(int now,int topn)
{
top[now]=topn;
dfn[now]=++dfns;rnk[dfns]=now;
if(!son[now])return;
dfs2(son[now],topn);
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(dfn[p])continue;
dfs2(p,p);
}
}
int lca(int x,int y)
{
while(top[x]^top[y])
{
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
return x;
}
int main()
{
n=re();m=re();s=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
dfs1(s,s);dfs2(s,s);
for(int i=1;i<=m;i++)
{
int x=re(),y=re();
wr(lca(x,y),'\n');
}
return 0;
}
上述是重链剖分,而实链剖分(LCT)也可以求 lca。
通过两次 access,第二次 access 的返回值即为两点的 lca。
const int inf=5e5+7;
int n,m,s;
struct Splay{
int fa,hz[2];
}T[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
void dfs(int now,int from)
{
T[now].fa=from;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs(p,now);
}
}
bool pd_son(int i)
{
return T[T[i].fa].hz[1]==i;
}
bool pd_rot(int i)
{
return (T[T[i].fa].hz[0]^i)&&(T[T[i].fa].hz[1]^i);
}
void rotate(int i)
{
int fa=T[i].fa,gf=T[fa].fa;
bool pdi=pd_son(i),pdf=pd_son(fa);
if(!pd_rot(fa))T[gf].hz[pdf]=i;T[i].fa=gf;
if(T[i].hz[pdi^1])T[T[i].hz[pdi^1]].fa=fa;
T[fa].hz[pdi]=T[i].hz[pdi^1];
T[i].hz[pdi^1]=fa,T[fa].fa=i;
}
void splay(int i)
{
for(int fa=T[i].fa;!pd_rot(i);rotate(i),fa=T[i].fa)
if(!pd_rot(fa))rotate(pd_son(i)^pd_son(fa)?i:fa);
}
int access(int i)
{
int s=0;
for(;i;s=i,i=T[i].fa)
splay(i),T[i].hz[1]=s;
return s;
}
int lca(int x,int y)
{
return access(x),access(y);
}
int main()
{
n=re();m=re();s=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
dfs(s,0);
for(int i=1;i<=m;i++)
{
int x=re(),y=re();
wr(lca(x,y),'\n');
}
return 0;
}
倍增
在说倍增之前,不得不提一句怎么暴力求 lca。
首先跳较深的点,将两个点拉到同一深度。
然后,两个点一起向上跳,直到重合。
但显然这样太慢了(毕竟是暴力嘛)。
其实,倍增就是一种将线性优化为 \(\log\) 的算法。它能通过适当的预处理,祛除大部分无用信息,从而降低复杂度。
先通过 dfs,记录下每个节点的父节点(\(2^0\) 级祖先),然后通过 \(2^j=2^{j-1}\times 2^{j-1}\),预处理出每个节点的 \(2^j\) 级祖先,
这样,不管是拉到同一深度还是共同上跳,都能通过比较深度,决定每次上跳是否越界。
最终就能求出来两点的 lca。
const int inf=5e5+7;
int n,m,s;
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int fa[inf][20],dep[inf];
void dfs(int now,int from)
{
fa[now][0]=from;
dep[now]=dep[from]+1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs(p,now);
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y])swap(x,y);
for(int i=19;i>=0;i--)
if(dep[fa[x][i]]>=dep[y])
x=fa[x][i];
if(x==y)return x;
for(int i=19;i>=0;i--)
if(fa[x][i]^fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
int main()
{
n=re();m=re();s=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
dfs(s,s);
for(int j=1;j<20;j++)
for(int i=1;i<=n;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
for(int i=1;i<=m;i++)
{
int x=re(),y=re();
wr(lca(x,y),'\n');
}
return 0;
}
Tarjan
与上述以及下述的算法不同,Tarjan 是一种离线算法,将所有的询问储存下来,统一处理。
Tarjan 通过 dfs,从根节点遍历整棵树。
每走到一个节点,我们需要对其进行以下三个操作:
- 标记当前节点已访问。
- 递归遍历子节点,并用并查集记录父子关系。
- 遍历所有与当前节点有关的查询操作。如果另一个节点已经访问,那么其与当前节点的 lca 就为其连通块的根。
至于原因,感性理解。
const int inf=5e5+7;
int n,m,s,fa[inf];
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
struct Lca{
int to,id;
Lca(int to,int id):
to(to),id(id){}
};
vector<Lca>q[inf];
int lca[inf];
bool vis[inf];
int find(int x){return (fa[x]^x)?(fa[x]=find(fa[x])):x;}
void tarjan(int now)
{
vis[now]=1;
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(vis[p])continue;
tarjan(p);fa[p]=now;
}
int len=q[now].size();
for(int i=0;i<len;i++)
{
int p=q[now][i].to;
if(!vis[p])continue;
lca[q[now][i].id]=find(p);
}
}
int main()
{
n=re();m=re();s=re();
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
for(int i=1;i<=m;i++)
{
int x=re(),y=re();
q[x].push_back(Lca(y,i));
q[y].push_back(Lca(x,i));
}
tarjan(s);
for(int i=1;i<=m;i++)
wr(lca[i],'\n');
return 0;
}
RMQ
一般来说,这里的静态 RMQ 问题,我们选择用 ST 表维护。
需要一个神奇的东西:欧拉序。
欧拉序能将一个子树变为序列上的一段完整的区间。具体求法就是递归进入到当前节点和每次从其子节点出来的时候加入到序列中。而一棵子树中,深度最小的点即为 lca。
问题就转化成了区间最小值,ST 表即可。
注意欧拉序的序列长度。
const int inf=5e5+7;
int n,m,s;
int fir[inf],nex[inf<<1],poi[inf<<1],cnt;
void ins(int x,int y)
{
nex[++cnt]=fir[x];
poi[cnt]=y;
fir[x]=cnt;
}
int dep[inf],sta[inf],olas;
struct Euler_Tour{
int ola,minn;
}lca[inf<<1][21];
Euler_Tour min(Euler_Tour a,Euler_Tour b)
{
return (a.minn>b.minn)?b:a;
}
void dfs(int now,int from)
{
sta[now]=++olas;
lca[olas][0].ola=now;
dep[now]=dep[from]+1;
lca[olas][0].minn=dep[now];
for(int i=fir[now];i;i=nex[i])
{
int p=poi[i];
if(p==from)continue;
dfs(p,now);
lca[++olas][0].ola=now;
lca[olas][0].minn=dep[now];
}
}
int main()
{
n=re();m=re();s=re();
for(int i=1;i<n;i++)
{
int u=re(),v=re();
ins(u,v),ins(v,u);
}
dfs(s,s);
for(int j=1;j<=21;j++)
for(int i=1;i+(1<<(j-1))<=olas;i++)
lca[i][j]=min(lca[i][j-1],lca[i+(1<<(j-1))][j-1]);
for(int i=1;i<=m;i++)
{
int l=sta[re()],r=sta[re()];
if(l>r)swap(l,r);int len=log2(r-l+1);
wr(min(lca[l][len],lca[r-(1<<len)+1][len]).ola,'\n');
}
return 0;
}