jdk1.8安装:
看了网上很多关于jdk1.8的安装,我觉得有时候会让人云里雾里,虽然自己可能配置成功,不过没有一套自己的思路,我结合自己的经验来说一下。
jdk在windows有两种安装方式,一种是解压缩包,还有一种是点击运行安装
注意两种方式选一个就行,一般选择解压缩,解压完成,然后配置环境变量就行!!!!!
1、首先谈关于解压缩包(比较简单):
首先是安装包:
1、直接用网盘下载:jdk1.8
2、官网下载需要注册账号:官网按照步骤来
点击Products

点击Java
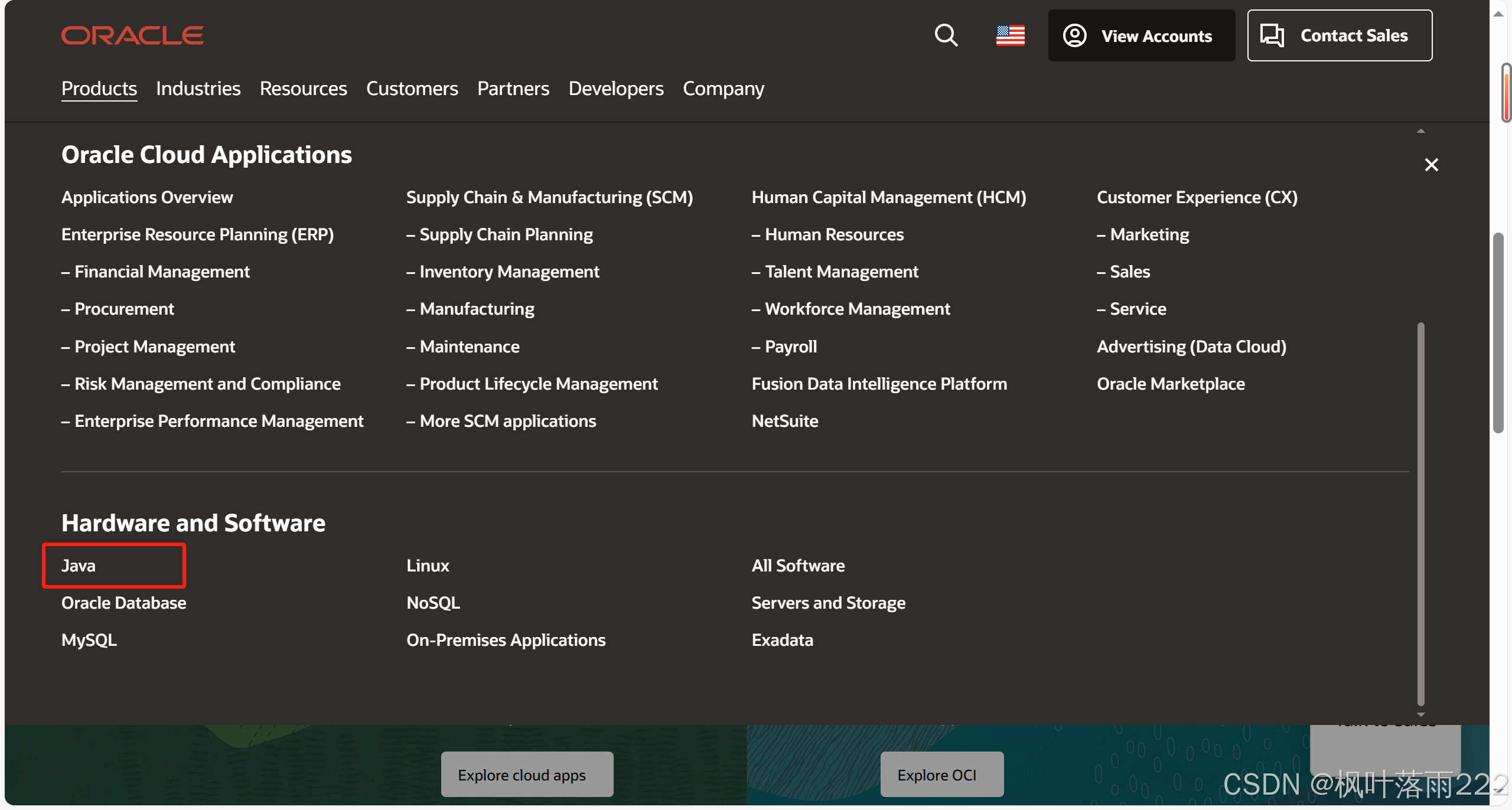
点击Download Java

点击进去后会显示最新版本的jdk
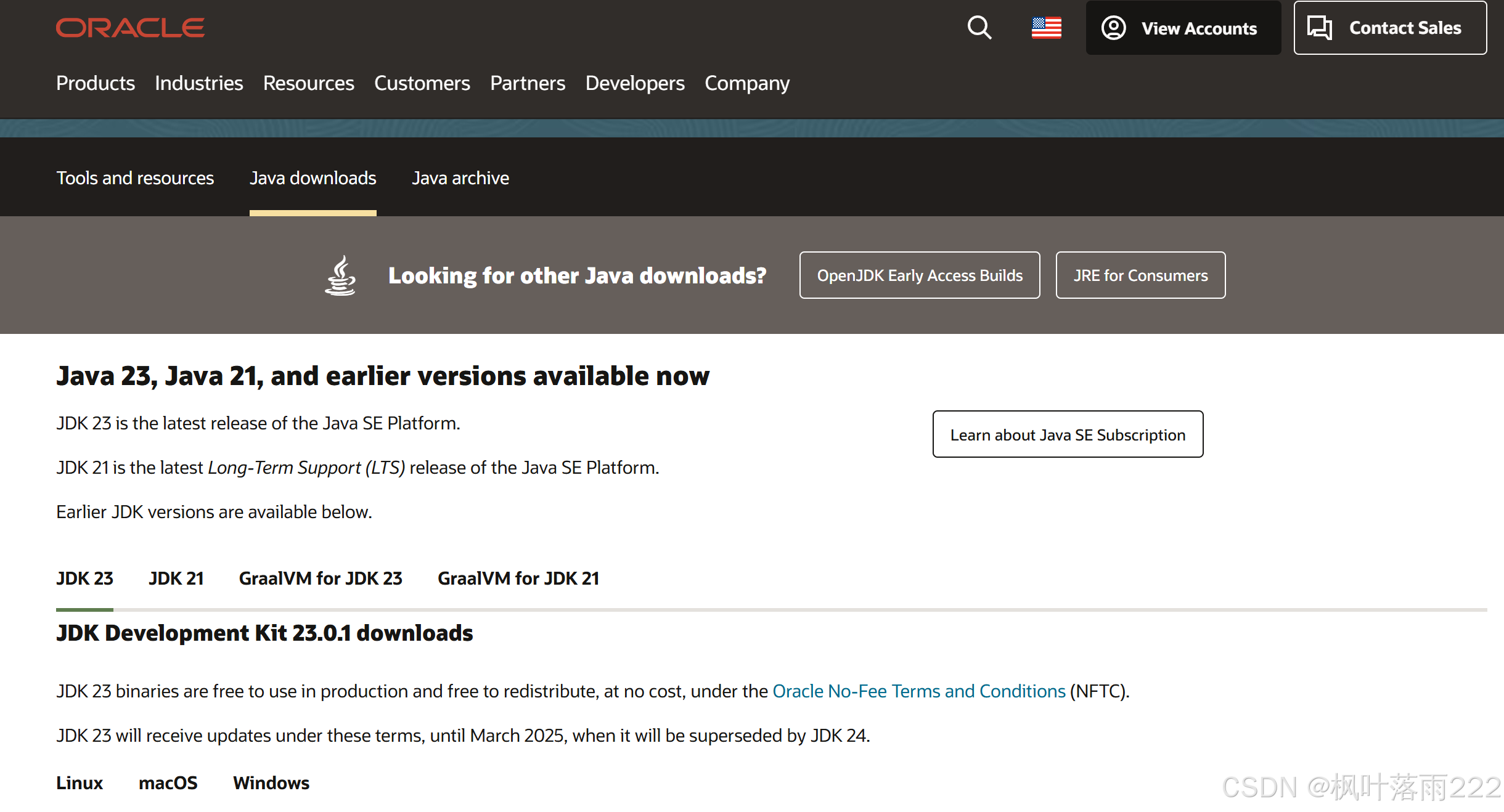
往下滑可以找到旧版jdk,我们可以选择稳定版本jdk1.8下载

解释一下可以用什么版本下载
| Product/file description | File size | Download |
|---|---|---|
| x86 Compressed Archive | 119.71 MB | |
| x86 Installer | 143.33 MB | |
| x64 Compressed Archive | 123.33 MB | |
| x64 Installer | 151.22 MB |
x86 Compressed Archive:
- 描述:适用于 32 位操作系统的 JDK 压缩文件(不需要安装,解压即可使用)
- 文件大小:119.71 MB
- 文件名:
jdk-8u431-windows-i586.zip- 适用平台:适用于 32 位 Windows 操作系统(x86)
x86 Installer:
- 描述:适用于 32 位操作系统的 JDK 安装程序(双击安装,自动配置环境)
- 文件大小:143.33 MB
- 文件名:
jdk-8u431-windows-i586.exe- 适用平台:适用于 32 位 Windows 操作系统(x86)
x64 Compressed Archive:
- 描述:适用于 64 位操作系统的 JDK 压缩文件(不需要安装,解压即可使用)
- 文件大小:123.33 MB
- 文件名:
jdk-8u431-windows-x64.zip- 适用平台:适用于 64 位 Windows 操作系统(x64)
x64 Installer:
- 描述:适用于 64 位操作系统的 JDK 安装程序(双击安装,自动配置环境)
- 文件大小:151.22 MB
- 文件名:
jdk-8u431-windows-x64.exe- 适用平台:适用于 64 位 Windows 操作系统(x64)
总结:
zip文件:是压缩包文件,适合手动解压后使用,无需安装,直接运行即可。exe文件:是可执行的安装程序,适合自动安装,安装时会帮你配置环境变量等。选择依据:
- 如果你使用的是 32 位操作系统,下载带有
i586或x86标识的文件。- 如果你使用的是 64 位操作系统,下载带有
x64标识的文件。- 如果你想手动解压并自己配置 Java 环境,可以选择 zip 文件。
- 如果你希望通过向导安装并自动配置 Java 环境,选择 exe 文件。
我选择x64 Compressed Archive,解压来配置(也就是解压缩包方式):
1、下载压缩包后直接解压得到文件夹(可以放到一个合适的地方):

2、然后直接开始配置环境变量
打开此电脑
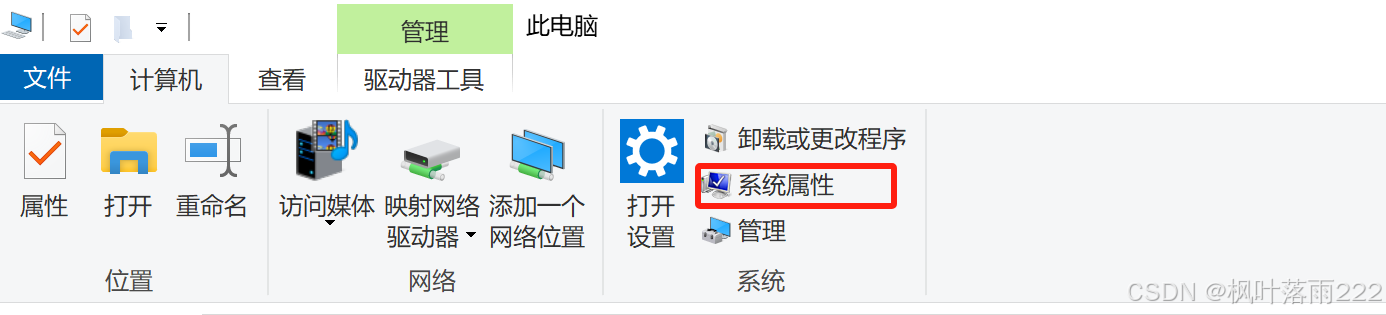
其次

然后
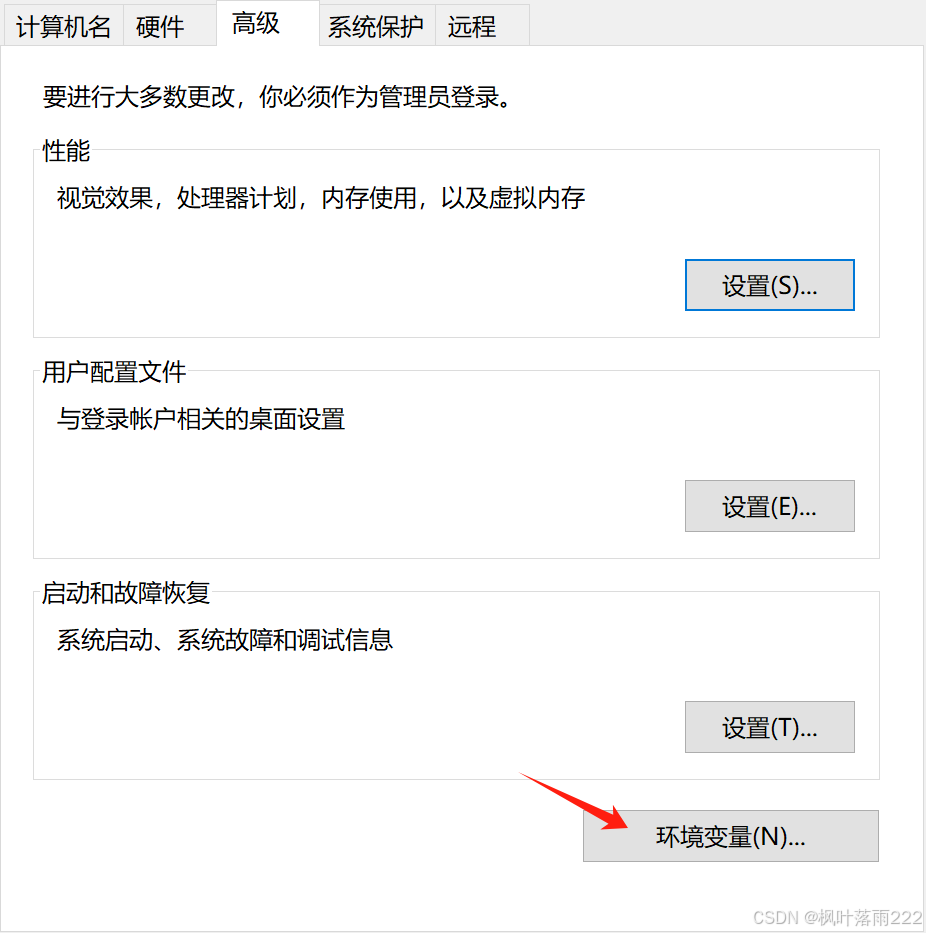
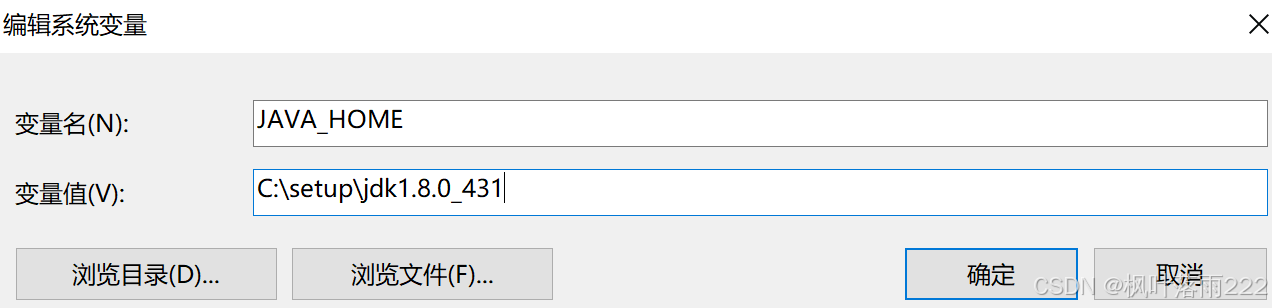
然后再,编辑系统变量,点击新建,输入变量名
JAVA_HOME,及你输入解压的地址即可(一般在D盘解压)
然后Path点击编辑

输入如下即可
%JAVA_HOME%\bin%JAVA_HOME%\jre\bin新建两个,然后点击确定即可(注意退出的过程必须每一步都点击确定)

环境配置完毕!!!!!!!
检查!!!!!!
java -version
该命令会显示你当前安装的 Java 版本信息。可以确认是否安装了 JDK,以及安装的是哪个版本的 JDK
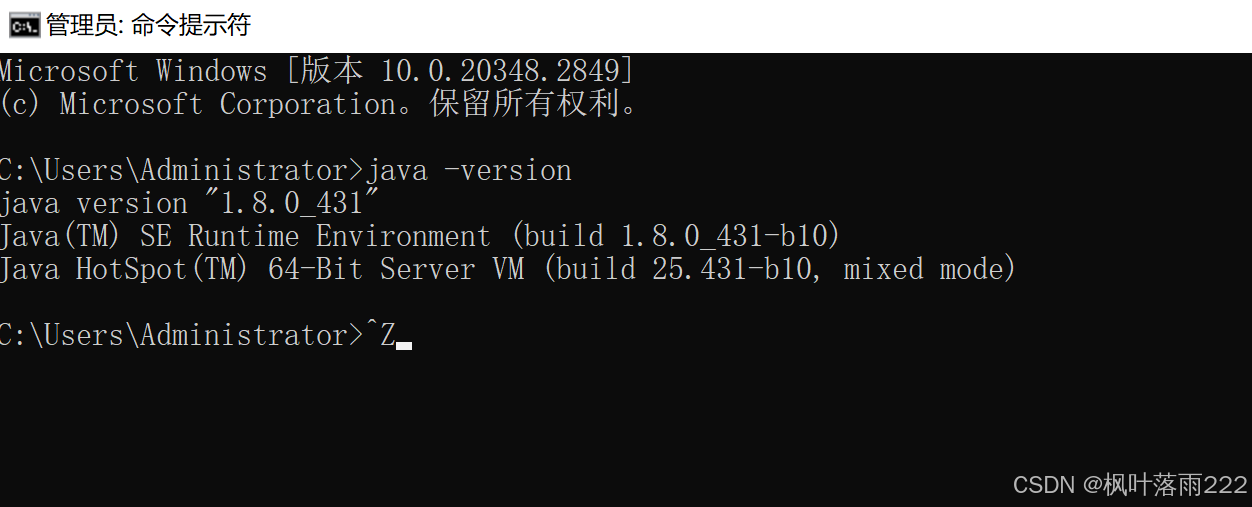
其次
javac -version
javac 是 Java 编译器,用于将 .java 源代码文件编译成 .class 字节码文件。通过这个命令可以确认 Java 编译工具是否已正确安装并能正常工作。

出现上面类似的两个界面,jdk完成安装环境变量配置成功!!!!!
补充一点有的同学有疑惑为什么别的博主会配置
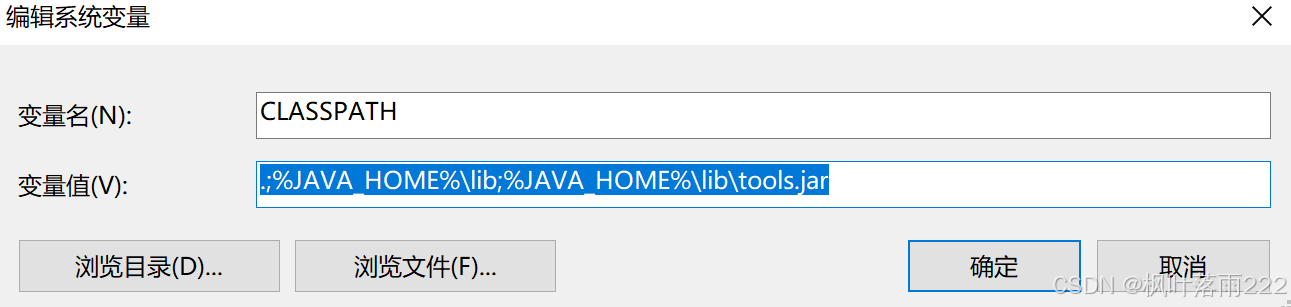
(在JDK1.5之后的版本,配置Java环境变量的时候我们不再需要配置classpath,只需要配置Java_Home以及path即可!)
2、谈关于直接安装:
选择最后一个
或者网盘下载
下载后就是一个安装包,直接点击运行安装即可

右击运行,下一步
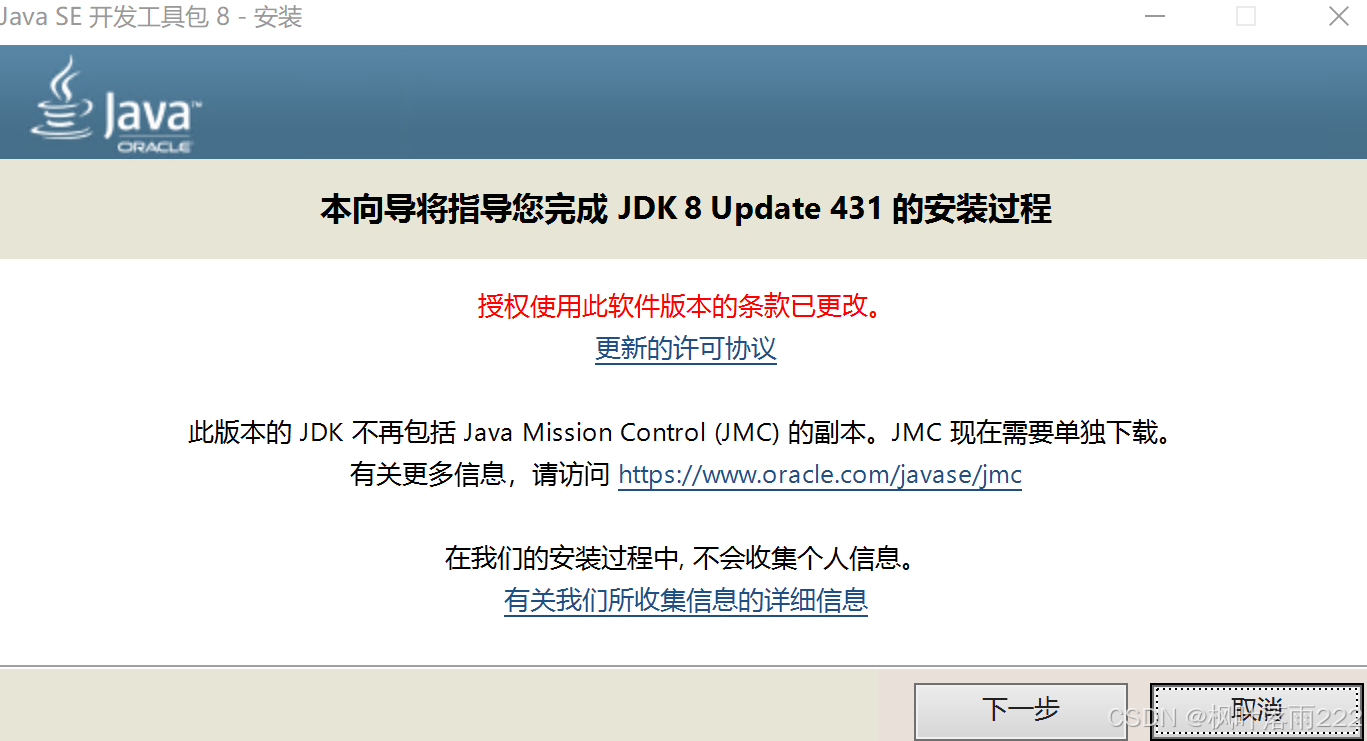
更改到D盘或者其它盘
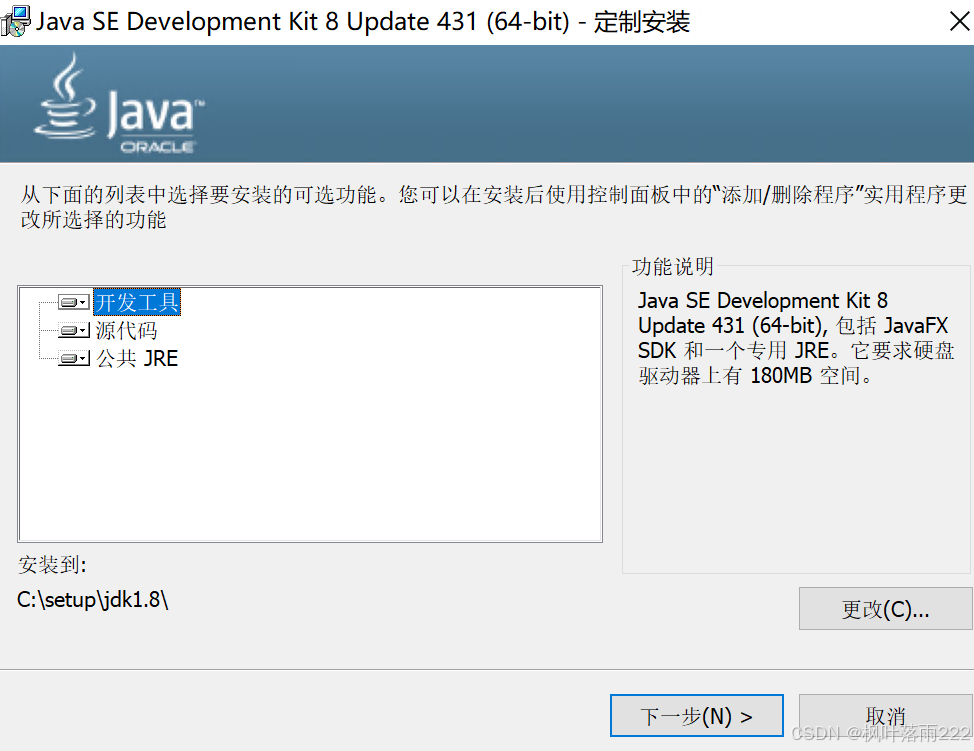
继续
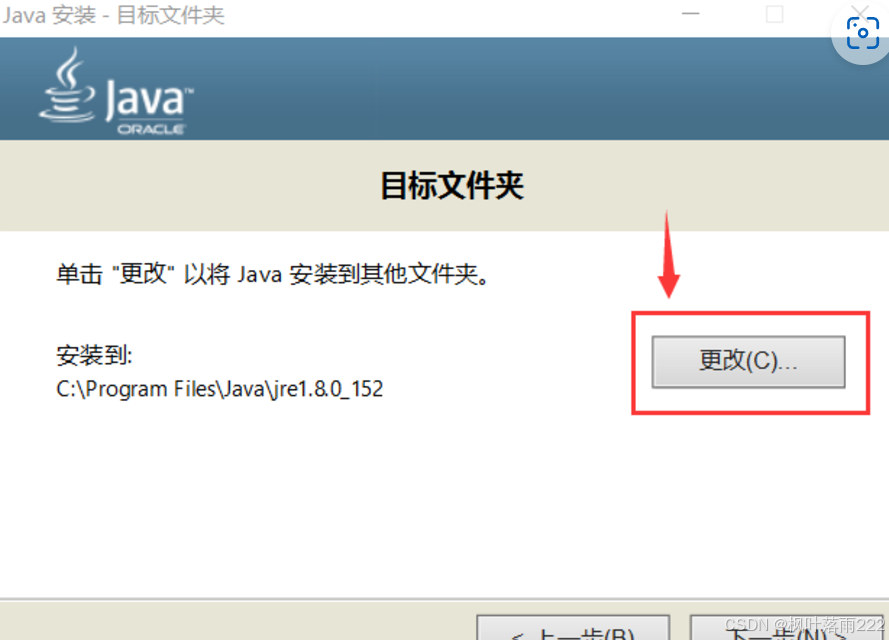
类似下面,新建一个jre文件夹
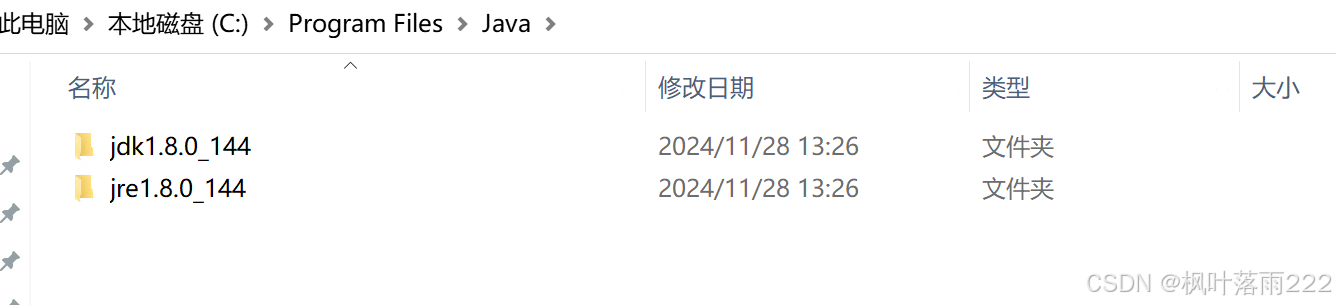
然后点击一步安装即可
注意:
你会发现这样安装的jdk1.8有两个jre,一个自带的,一个刚刚安装的【不用管、知道就好】
JDK 自带的 JRE:
- 位于 JDK 安装目录下。
- 用于支持 JDK 内部的开发工具和运行时环境。
- 一般不会单独使用,因为它是 JDK 的一部分。
独立安装的 JRE:
- 用于系统中的 Java 程序(比如一些需要 Java 支持的第三方应用、Web 浏览器插件等)。
- 它是独立于 JDK 之外的,主要用于支持运行 Java 应用。
- 你可以通过
JAVA_HOME和PATH环境变量指定使用哪个 JRE。
然后接着配置环境变量:
同理:


当然查看配置是否正确也是:
java -versionjavac -version如果只想配置成功,就用第一张解压的更快!!!!
标签:解压,jdk1.8,Java,JDK,jdk,x64,教学,安装 From: https://blog.csdn.net/qq_56947957/article/details/144257541