你的团队是否也在为工作效率发愁？

1. 为什么项目进度管理效率低下成为普遍问题？

在如今竞争激烈的商业环境中，项目进度管理已经成为企业成功与否的关键因素之一。然而，许多企业和团队仍然面临着工作效率低下的问题，尤其在多任务、高复杂度项目的管理中。这种低效不仅影响了团队士气，还可能导致项目的延期、预算超支，甚至客户的不满。

为什么会出现这种情况呢？从实际的工作场景来看，项目进程中的低效率往往是由于信息的传递不畅、任务优先级模糊、团队协作缺乏透明度等问题所导致。虽然很多企业和团队已经采用了各种管理工具，但这些工具并不能真正解决效率低下的问题。

2. 工作效率慢的根本原因是什么？

工作效率慢并不是一个简单的“懒惰”问题，而是多种因素交织的结果。以下是几个常见的原因：

缺乏清晰的任务规划

在项目管理中，任务的规划和优先级的设定至关重要。如果团队成员不清楚自己的工作重点和每个任务的紧急程度，工作容易陷入“忙而无果”的状态，导致整体进度滞后。

信息不对称

许多团队在项目执行过程中会遇到信息滞后的问题，尤其是当项目成员分散在不同地点或部门时。缺乏实时信息共享会造成任务重叠、时间浪费、甚至项目方向的误解。

协作不顺畅

高效的协作是高效工作的重要保证，但许多团队缺乏有效的协作工具或流程，导致任务交接不清晰、沟通不及时，最终拖慢项目进度。

进度追踪和反馈机制不完善

项目进度需要持续跟踪与反馈，如果没有一个清晰、透明的进度追踪系统，团队成员很难知道自己和他人的工作进展，从而容易在关键任务上出现拖延。

任务过度分散

在一些较大的项目中，任务可能被拆分成了过多的小部分，导致团队成员忙于处理琐碎任务，反而忽略了整体目标的推进。这种任务过度分散往往让团队无法聚焦在最重要的工作上，拖慢了整体进度。

3. 如何有效提升工作效率并解决低效问题？

针对上述问题，我们可以采取一系列有效的措施，来提升团队的工作效率：

任务清晰规划与优先级排序

通过明确每个任务的目标和优先级，可以帮助团队成员更好地集中精力处理最重要的工作。使用任务管理工具，按照紧急程度和重要性排序任务，能避免人员盲目忙碌。

信息流动畅通无阻

一个高效的团队需要确保信息流通畅通无阻。通过实时更新的共享平台，确保所有相关人员都能随时访问和更新任务信息，减少信息滞后带来的沟通误差。

优化协作流程

实施高效的团队协作工具，能够使得任务和反馈在团队内快速流转。团队成员可以随时查看当前任务的状态，进行沟通和协作，确保没有信息遗漏，进而提高工作效率。

进度跟踪与透明反馈

实时的进度跟踪和透明的反馈机制能够帮助团队成员了解项目整体进展，从而及时调整自己的工作。定期的项目检查和反馈会议也是有效的提升团队协作效率的方式。

聚焦核心任务

有效地将任务拆解成适当的大小，并确保团队成员能够集中精力处理最重要的工作，避免任务过度分散，导致项目进度拖慢。

4. 板栗看板：如何帮助提升团队工作效率？

在所有提升工作效率的方法中，借助高效的工具来优化任务管理、进度追踪和团队协作，往往是最直接且有效的方式之一。而板栗看板正是这样一款针对团队协作和项目管理优化的工具，它能够为企业和团队解决工作效率慢的多种根本问题。

清晰的任务视图

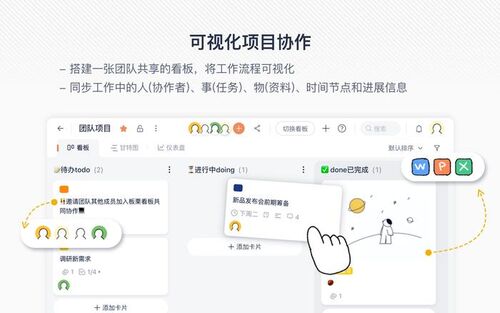
板栗看板提供了看板视图，使得任务的每个状态一目了然。通过自定义的任务板块（如待办、进行中、已完成等），每个团队成员都可以清晰看到自己和他人的任务进展，避免了任务执行中的混乱与重复。

实时更新与协作

板栗看板支持实时任务更新与信息共享，确保团队成员始终在同一信息基础上展开工作，消除信息滞后的问题。任务进展、状态更新、团队反馈等信息能够立即反馈到所有成员，大大提高了沟通效率。

任务优先级与进度追踪

通过板栗看板，企业和团队可以为每个任务设置优先级，并通过看板的状态追踪功能，实时查看任务的执行情况。无论是项目经理还是团队成员，都能清楚地了解任务进展，并根据需要做出调整。

灵活的任务拆解

板栗看板可以帮助团队灵活拆解任务，将复杂的工作分解成具体的子任务，避免过度分散的情况。同时，通过任务分配，团队成员可以更加专注地完成核心任务，从而提高整体工作效率。

强大的团队协作功能

板栗看板的任务讨论和文件共享功能，使得团队成员在处理任务时能快速沟通、交换意见，不必担心信息滞后或遗漏。每个任务都可以配备明确的负责人，确保每个成员都能及时处理自己的任务。

5. 结论：通过板栗看板实现高效的项目管理与任务协作

总的来说，提升项目进度管理效率的关键在于清晰的任务规划、信息的高效流通、协作的顺畅和进度的透明追踪。而板栗看板通过其强大的任务管理和进度跟踪功能，能够有效解决目前很多团队在项目管理中遇到的效率低下问题。它为企业提供了一个集任务管理、进度追踪、团队协作于一体的智能平台，帮助团队集中精力、高效执行任务，从而提升整个项目的完成效率。

如果你的团队也面临着工作效率慢、项目进度滞后的问题，板栗看板无疑是一个值得尝试的解决方案。