声明
本文章中所有内容仅供学习交流使用,不用于其他任何目的,不提供完整代码,抓包内容、敏感网址、数据接口等均已做脱敏处理,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!
本文章未经许可禁止转载,禁止任何修改后二次传播,擅自使用本文讲解的技术而导致的任何意外,作者均不负责,若有侵权,请在公众号【K哥爬虫】联系作者立即删除!
前言
最近有粉丝反馈,在处理业务网站的时候,碰到了某里的验证码,但是又和大伙所熟知的 226、227 不一样:

其实这是某里 v2 验证码,相较于 228、231 这种旗舰产品,之前使用 v2 的网站并不是很多,不过最近有多起来的趋势。
部分小伙伴可能看到了某里系的验证码,就认为解决不了,直接放弃,其实都没有那么复杂,不说全纯算还原,至少补环境是可以尝试一下的。v2 验证码有很多类型,滑动的版本变动最频繁,1.1.0 一直到现在的 1.1.10,再过两天可能又是新的,解决流程其实都大差不差,本文就逆向分析一下某里 v2 滑动验证码,仅供参考:
逆向目标
- 目标:某里 v2 滑动验证码
- 网址:想要研究的小伙伴,私聊
抓包分析
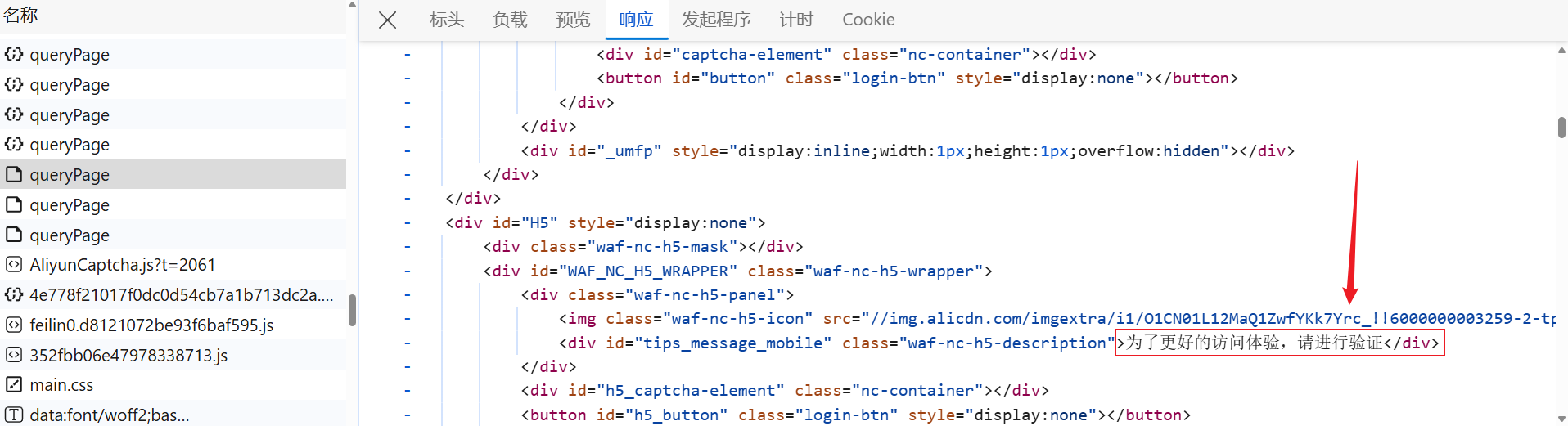
本案例的网站,不停地点下一页就会触发验证码,也可以直接访问我前文给到的网址(如果响应 HTTP Status 405 – Method Not Allowed 就是指纹黑了)。queryPage 接口正常会返回公告相关数据,触发了验证码,响应内容就会提示需要验证:
主要需要关注四个接口,前后请求了两次 4e778xxx.captcha-pro-open.aliyuncs.com(提交的参数不同)接口,第一次获取 DeviceConfig、RequestId 参数,用于后续验证,StaticPath 即版本号。请求参数中有个 SignatureMethod,值为 HMAC-SHA1,这着就像是有啥参数是经过这个算法加密的:
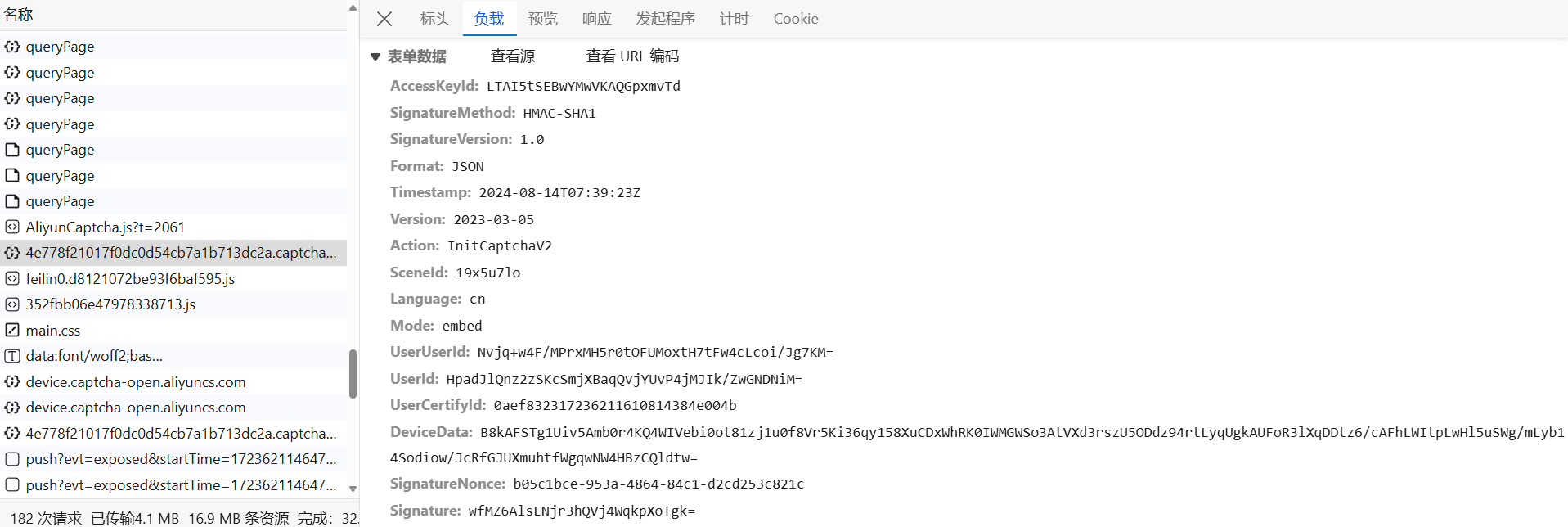
- AccessKeyId:固定值,不同接口不一样;
- UserUserId、UserId、UserCertifyId:queryPage 接口触发验证码时,响应返回;
- DeviceData:设备信息;
- SignatureNonce:类 UUID,后文分析;
- Signature:对相关请求参数进行加密、编码,后文分析。
第二次请求,即最终的验证码校验,获取校验结果及相关参数:
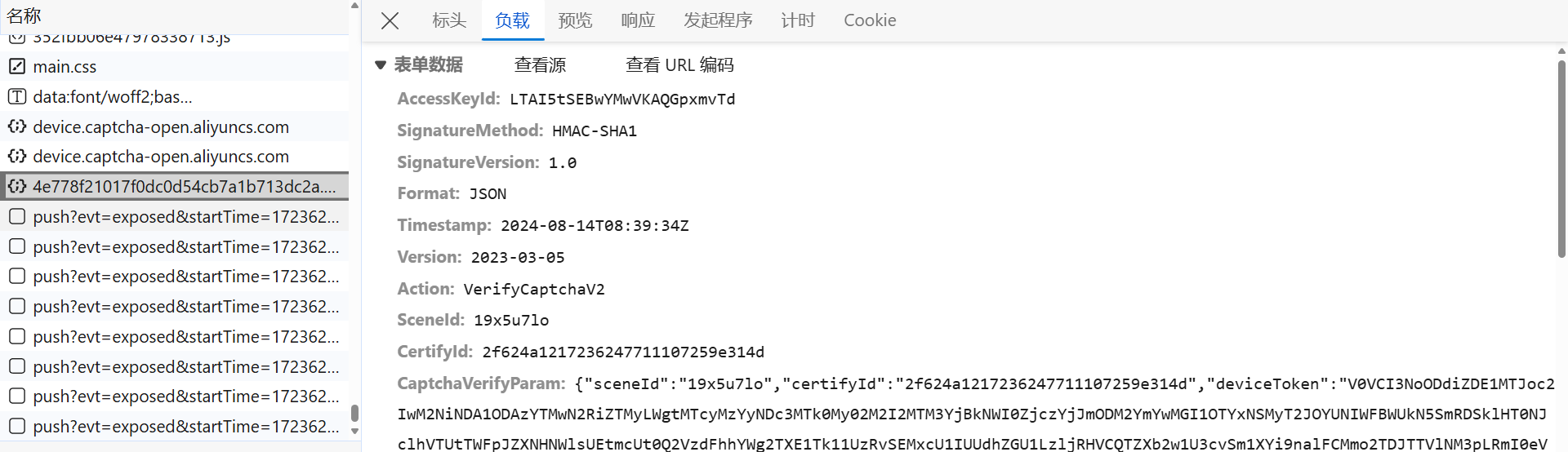
- CertifyId:queryPage 接口触发验证码时,响应返回,即 traceid;
- CaptchaVerifyParam:一些校验参数,包括各种环境、指纹、轨迹等等,后文分析。
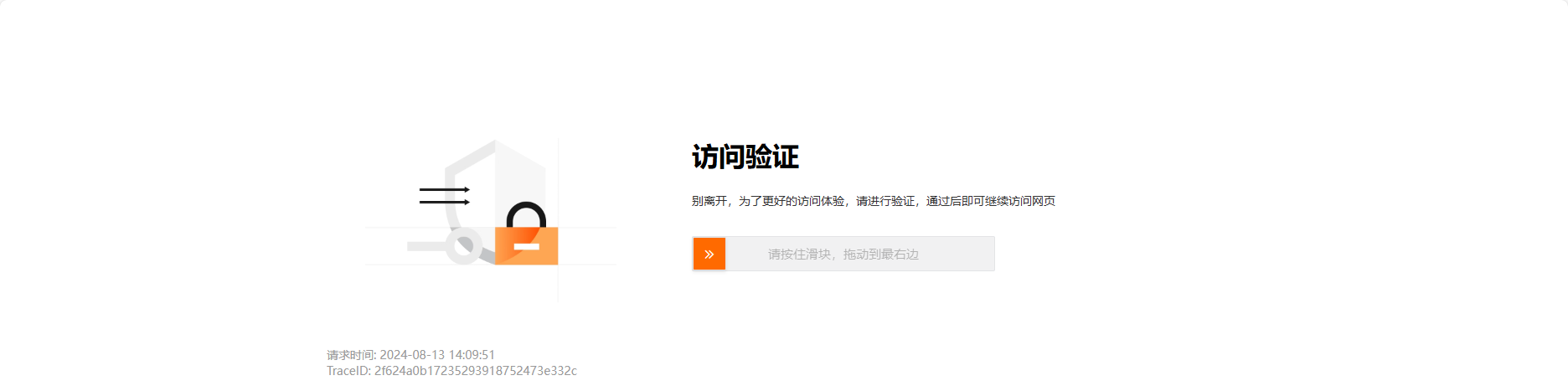
验证失败,VerifyCode 为 F001、F002:
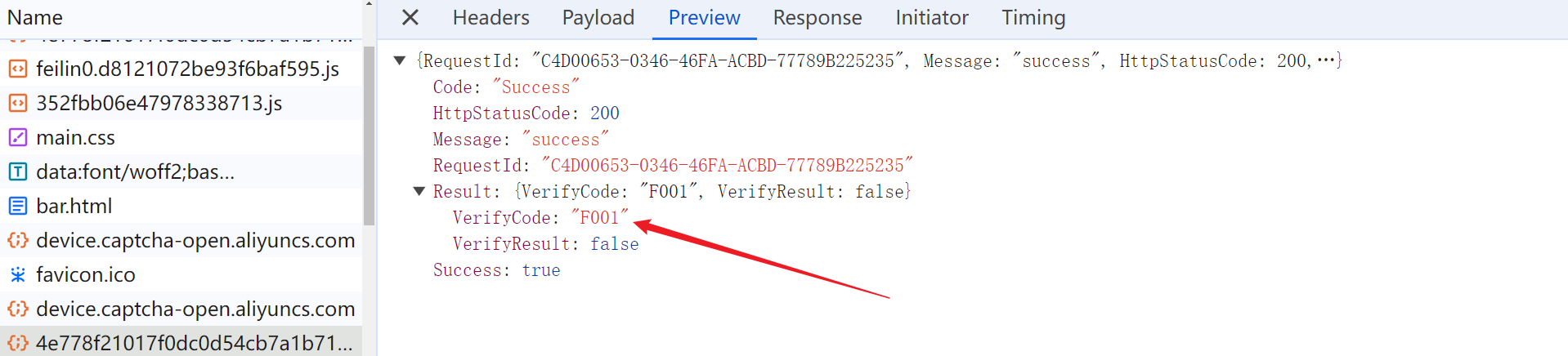
验证成功,VerifyCode 为 T001:

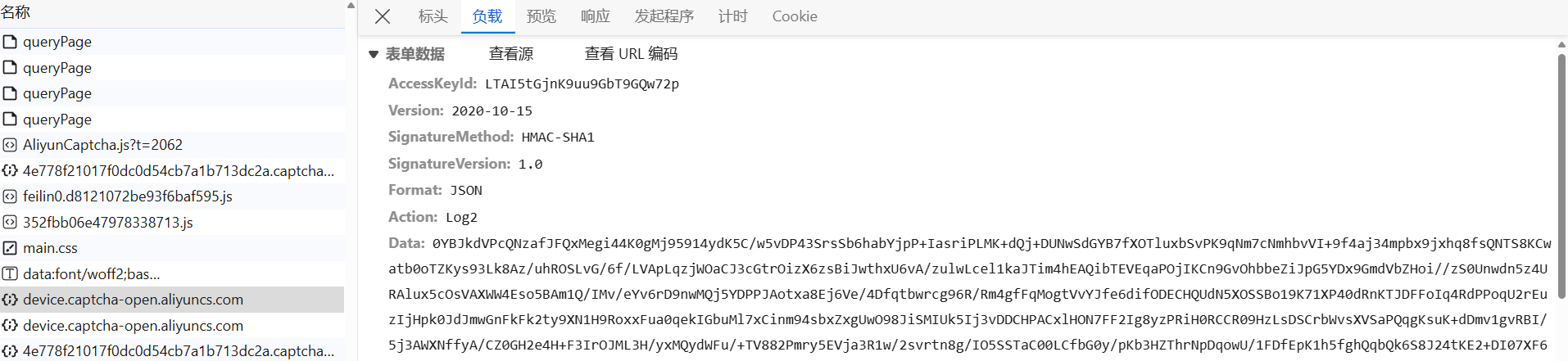
中间请求了两次 device.captcha-open.aliyuncs.com(Log2、Log3)接口,进行设备、轨迹验证(该站校验了 Log2),Data 参数经过加密处理,后文分析:
逆向分析
SignatureNonce
触发验证码,抓包后会看到,第一个接口 4e778fxxx.aliyuncs.com 是 xhr 类型的,直接去源代码(Sources)中下个 xhr 断点,刷新网页重新触发验证码即会断住。此时请求参数都已经生成了:
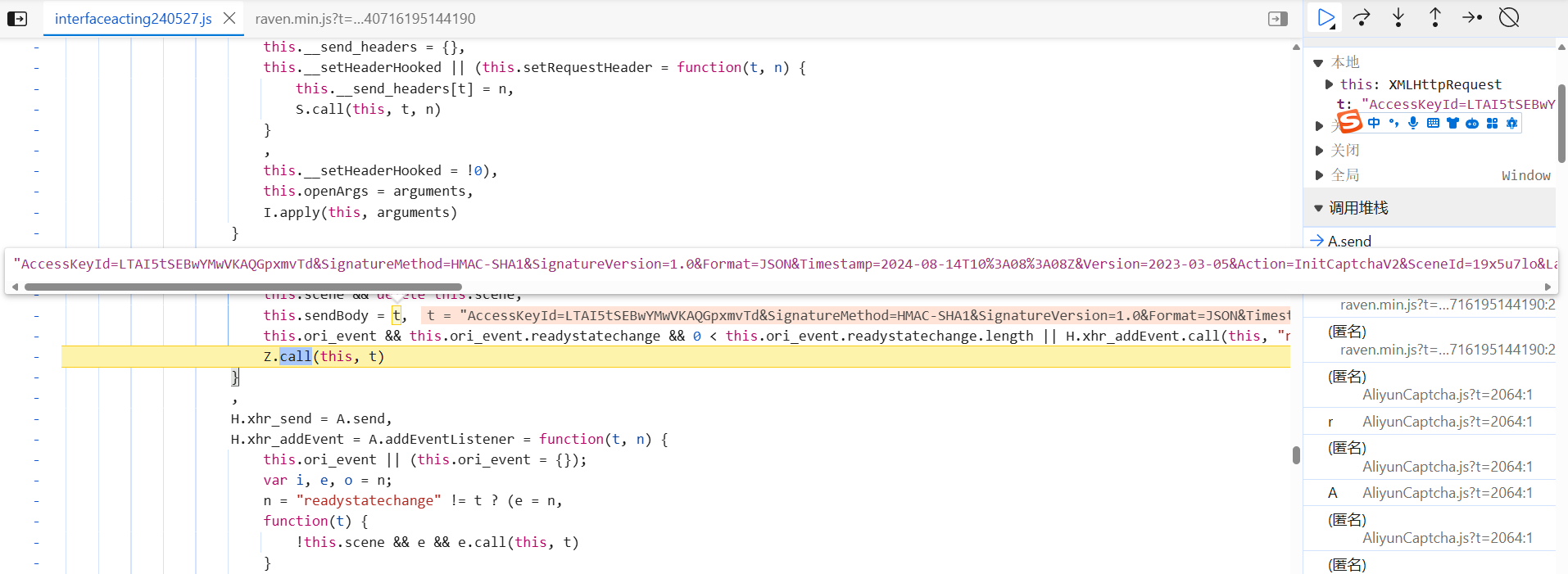
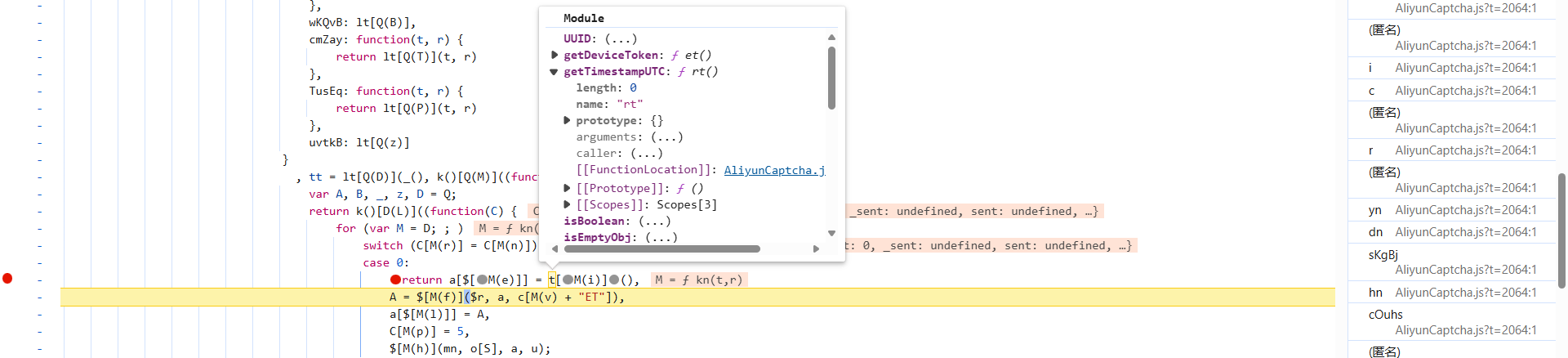
接着向上跟栈,跟到 AliyunCaptcha.js 文件中(有几套,可以固定一下),下图即 SignatureNonce 的加密位置,跟进到 t[M(i)] 中,将算法扣下来即可:

Signature
加密位置就在 SignatureNonce 下面,就是 A:
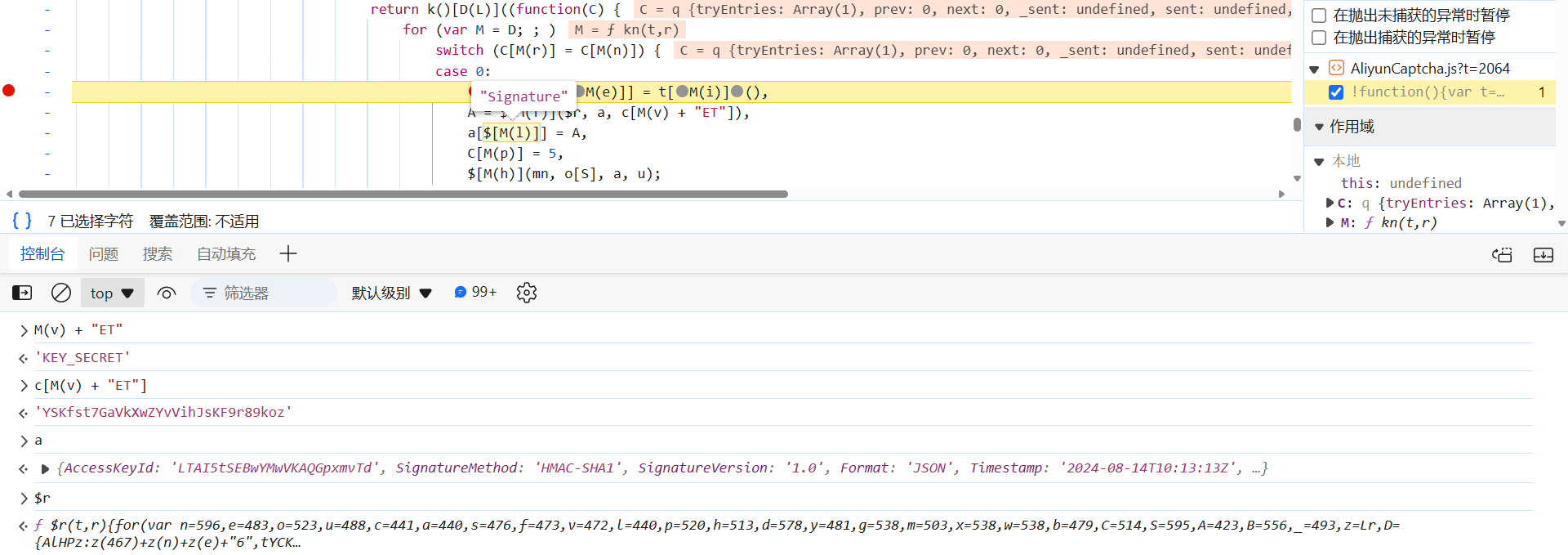
A = $[M(f)]($r, a, c[M(v) + "ET"])
- c[M(v) + "ET"]:加密的密钥,固定值;
- a:相关请求参数;
- $r:加密函数。
直接跟到加密函数 $r 中去看看,经典的 switch 语句,按照下图顺序,跳来跳去,饶了一大圈,实际上最后一个,才是关键的算法:
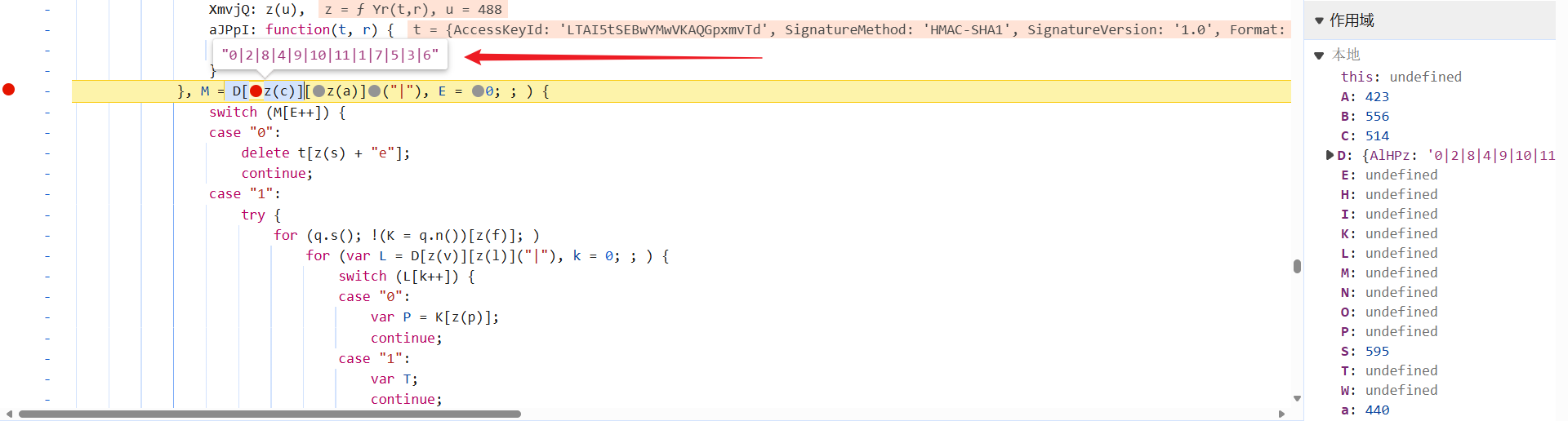
控制台打印一下,关键的加密函数为 rn,传了两个参数生成了 Signature 的值;请求参数拼接后,再经过 url 编码得到的 N;最终的 key 就是 YSKfst7GaVkXwZYvVihJsKF9r89koz&:
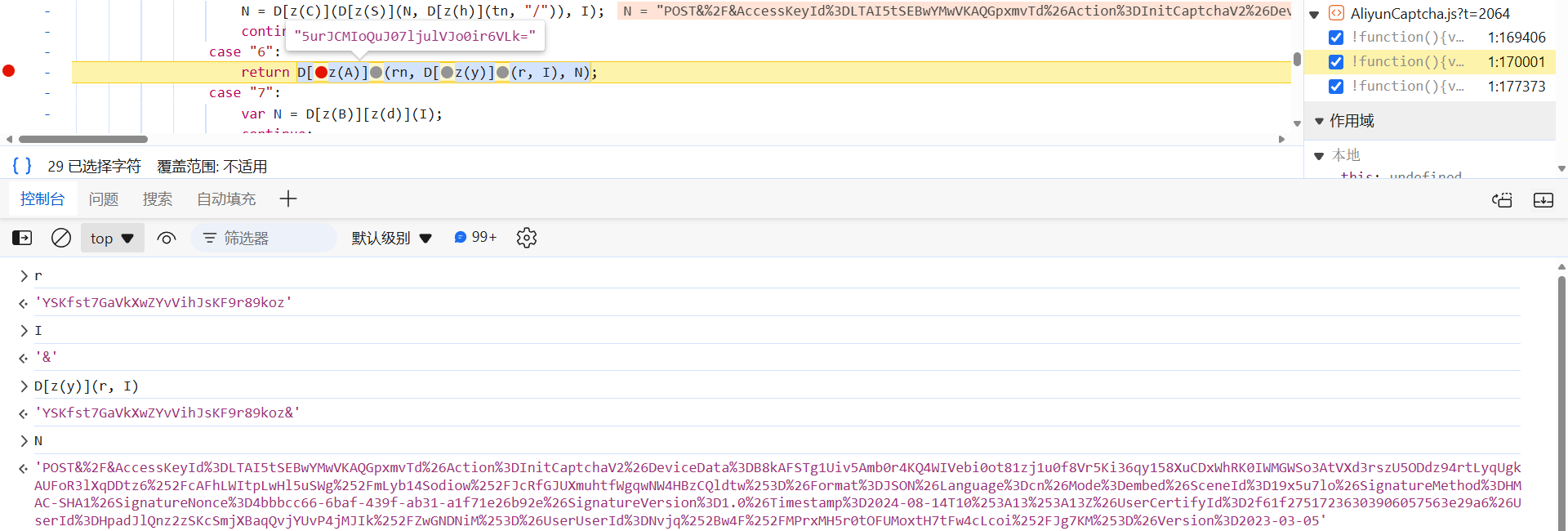
跟进去,代码如下:
function rn(t, r) {
var n = 477
, e = 511
, i = Lr
, o = Er()[i(n)](r, t);
return Ir[i(e) + "y"](o)
}
Ir[i(e) + "y"](o) 即 Signature 的值,先跟到 Er()[i(n)] 中去,代码如下,HMAC 初始化了一个带有指定哈希算法和秘钥的对象,n 即密钥 YSKfst7GaVkXwZYvVihJsKF9r89koz&,r 为消息数据,也就是经过编码后的相关请求参数:
new l.HMAC.init(t, n).finalize(r)
从下图中可以看到,HMAC 摘要的字节长度 sigBytes 为 20,印证了前文的猜想,这里采用的就是 HMAC-SHA1 摘要算法(HMAC-SHA-256 为 32 字节,HMAC-SHA-512 为 64 字节),用 toString() 方法能将其转成十六进制的字符串,也就是最终的值:
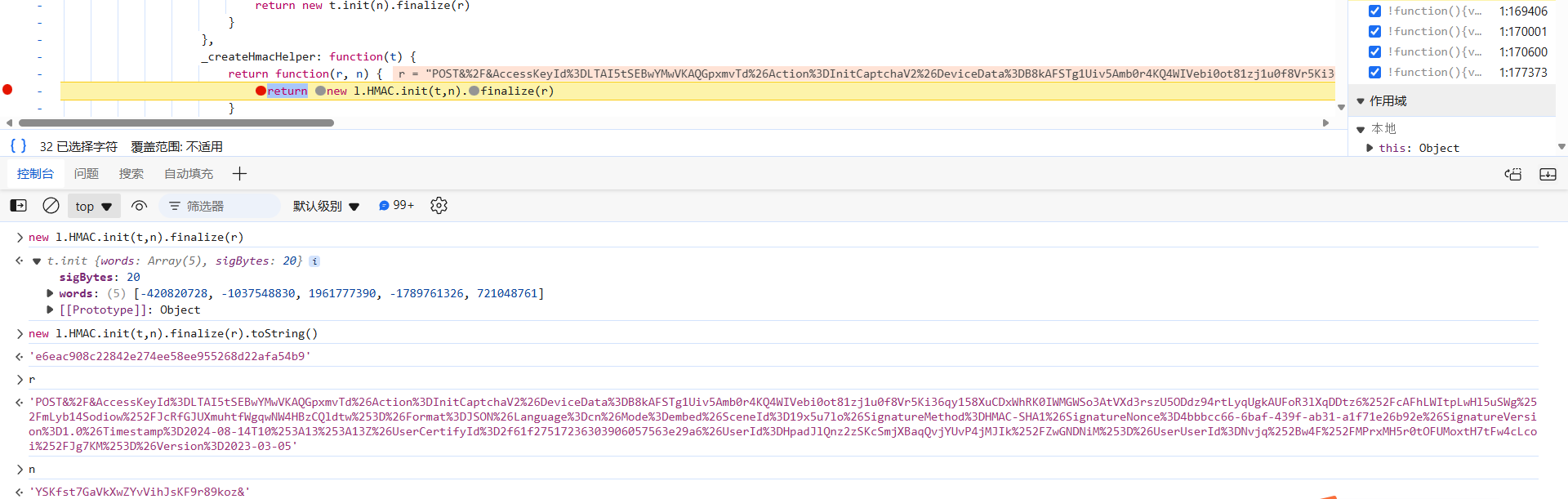
还可以用下面这种方式转,方法很多:
const hmacResult = {
"words": [-420820728, -1037548830, 1961777390, -1789761326, 721048761],
"sigBytes": 20
};
const hex = hmacResult.words.map(word =>
(word >>> 0).toString(16).padStart(8, '0')
).join('');
console.log(hex); // 输出对应的十六进制字符串
再去K哥工具库对比一下,确认是 HMAC-SHA1 了:
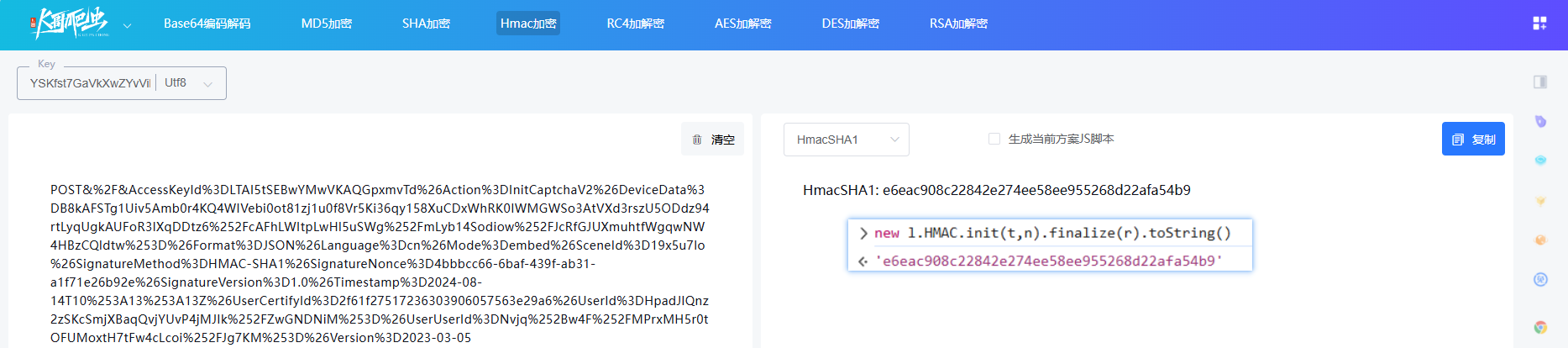
在线 HMAC 加密工具:https://www.kgtools.cn/secret/hmac
但是很明显,这并不是 Signature 的值,也就是还经过了别的处理。最后再跟到 Ir[i(e) + "y"] 中去看看,发现还经过了 base64 编码,当然,不是直接编码的 HMAC-SHA1 后的结果,这里是对 words 数组(包含了 HMAC 运算的结果)编码后得到的:

那这该怎么处理呢?逆向思维一下,先通过密钥,将字符串加密,将加密后的十六进制字符串转换为 Buffer,写进 words,再进行上面的计算即可。
参数都处理完,请求第一个接口,若响应如下,需要注意些细节,比如请求参数是否正确,以及编码问题:
"Message":"Specified signature is not matched with our calculation!"
Timestamp 参数也不能随便乱写,不然同样拿不到正确的结果:
"Message":"Timestamp is illegal!"
扣下来即可:
device.captcha-open.aliyuncs.com 接口也会需要 SignatureNonce 和 Signature,大差不差,只不过请求参数和 key 不一样而已,流程类似,跟栈就能找到,不赘述了。
Data
设备认证参数,环境风控点。同样跟栈下断点分析,跟到此处时,发现 Data 的值已经生成了:
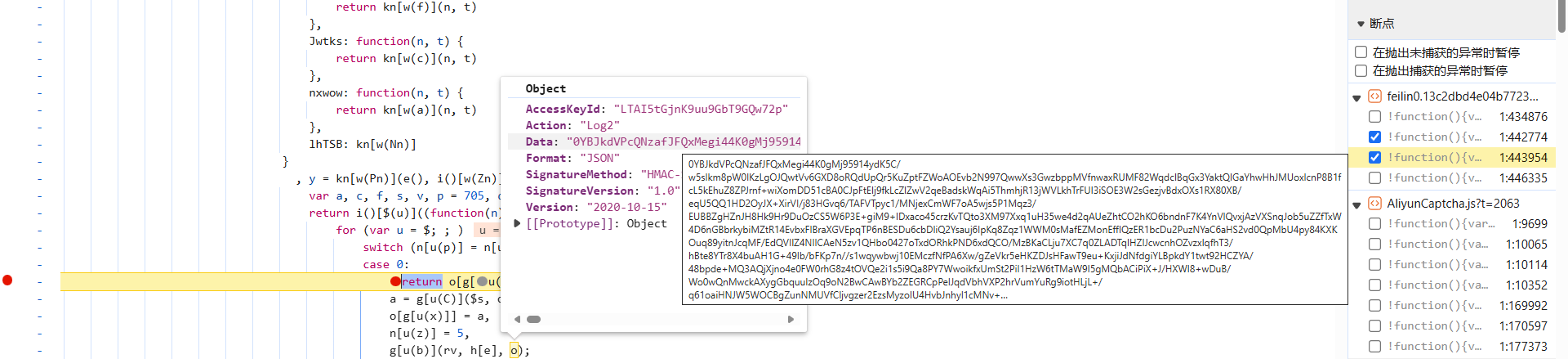
这里的 o 对象中明显存储的是相关的请求参数,往上跟 o 就会发现,Data 定义在下图所示位置:
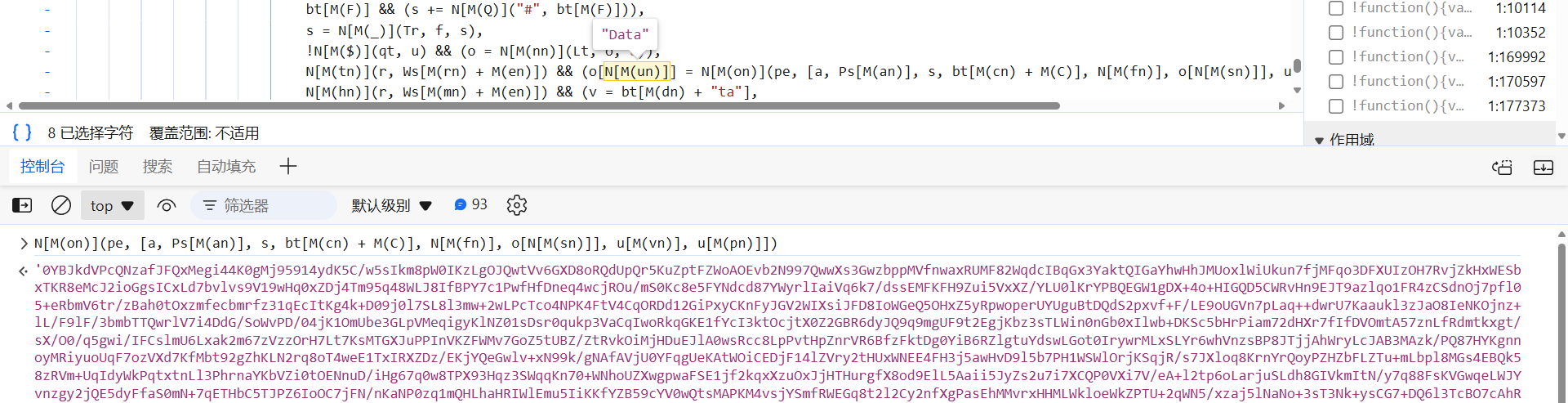
pe([a, Ps["WEB"], s, bt["APP_VERSION"], "CLOUD", o["GatherCost"], u["Type"], u["Data"]])
部分是定值,WEB_AES_SECRET_KEY,可以跟一下看看,比如 s,走到算法里,插桩打印一下。可以看到,前面两个参数加密生成的 s,第一个值为 key,AES 解密后得到的,非定值:
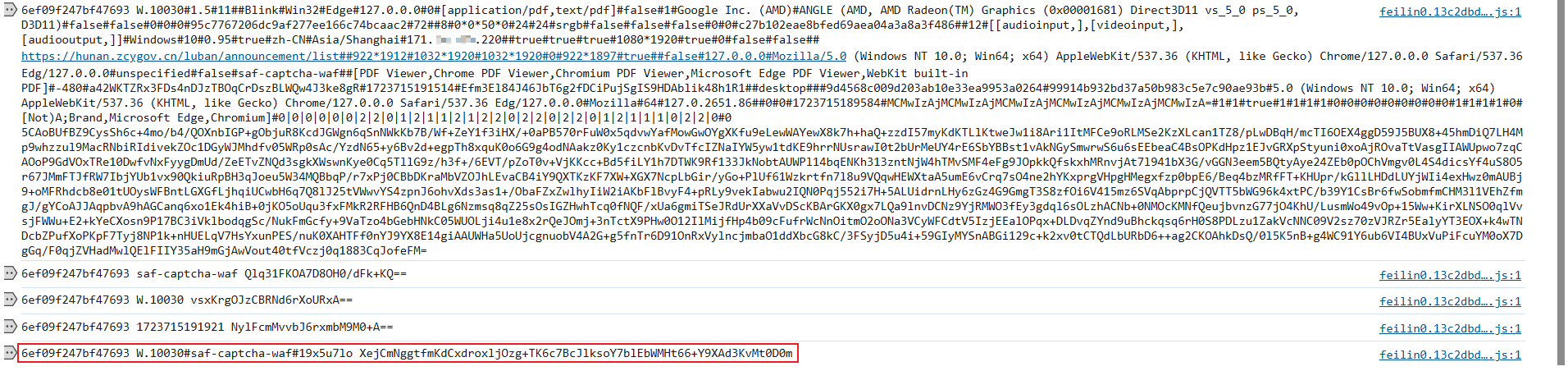
其解密的 key 又和 secretKey 有关,插桩观察,再打条件断点,发现是第一个接口返回的 DeviceConfig 解密后得到的(还传了 ip 校验),套娃,需要注意的是,几个加解密的 key 并非都是一样的:
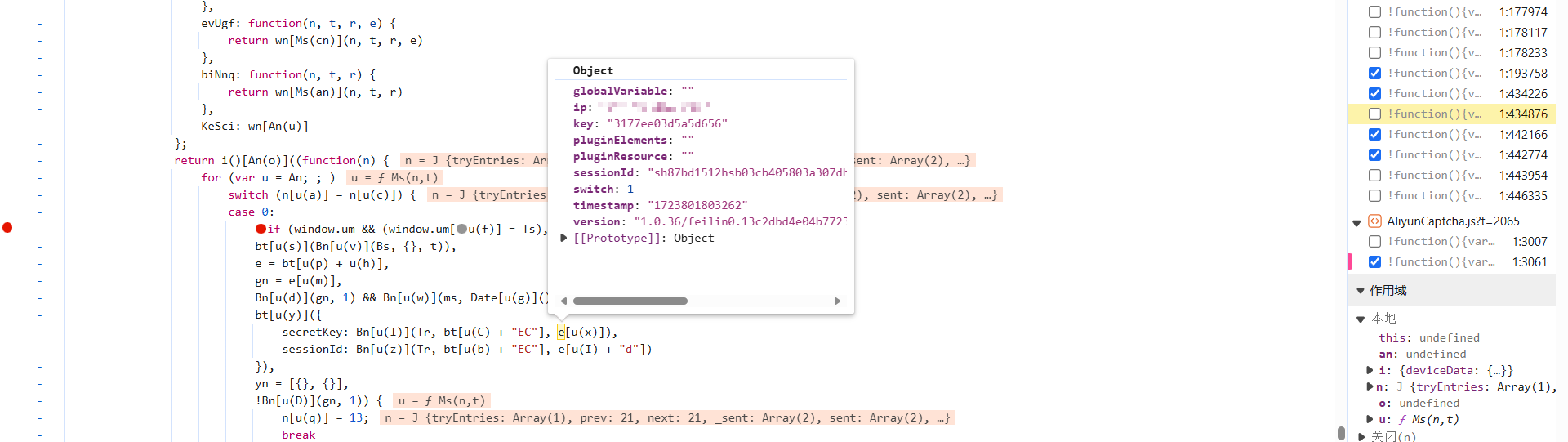
前文截图部分的日志,最上面还打印出了一些环境,包括 User-Agent、时区、ip 等等,后面会用到。s 本身就是 AES 加密,iv 之类也好找:

这个 u["Data"] 也并非固定值,需要跟一下:

往上跟栈后会发现,其是由一些环境参数拼接后加密生成:
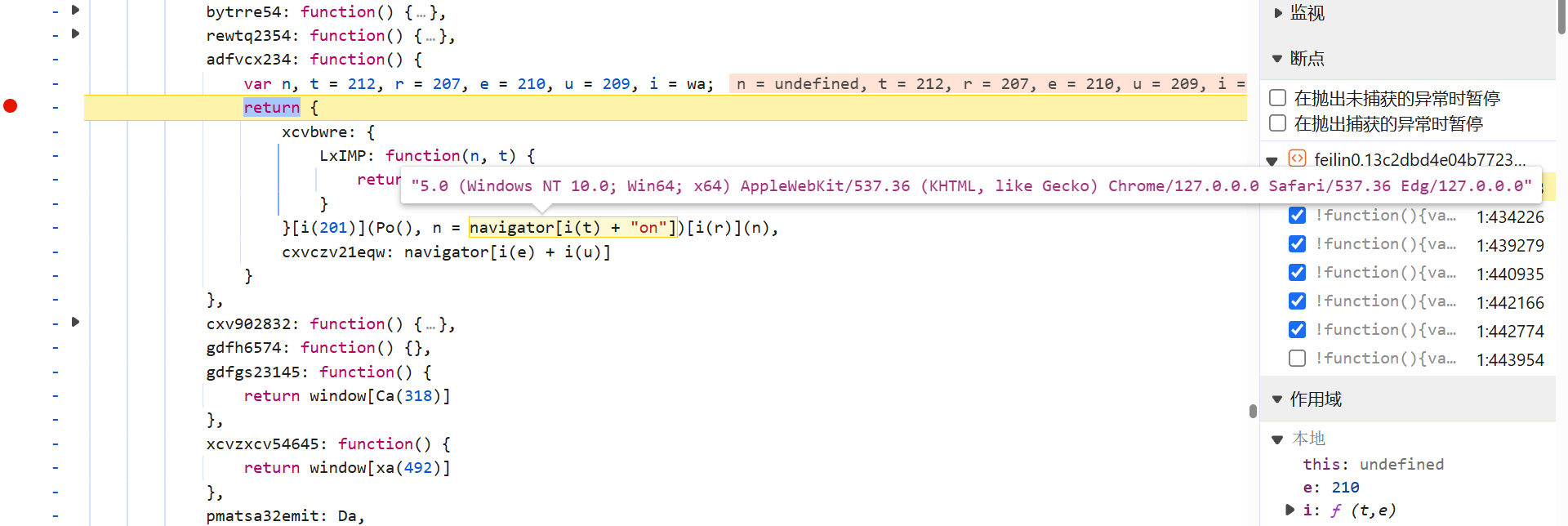
无非也是 AES 的加解密,key 套 key,都较容易找到。
第二次设备验证,Data 值的位置就在第一次的附近,整体和第一次的大差不差:
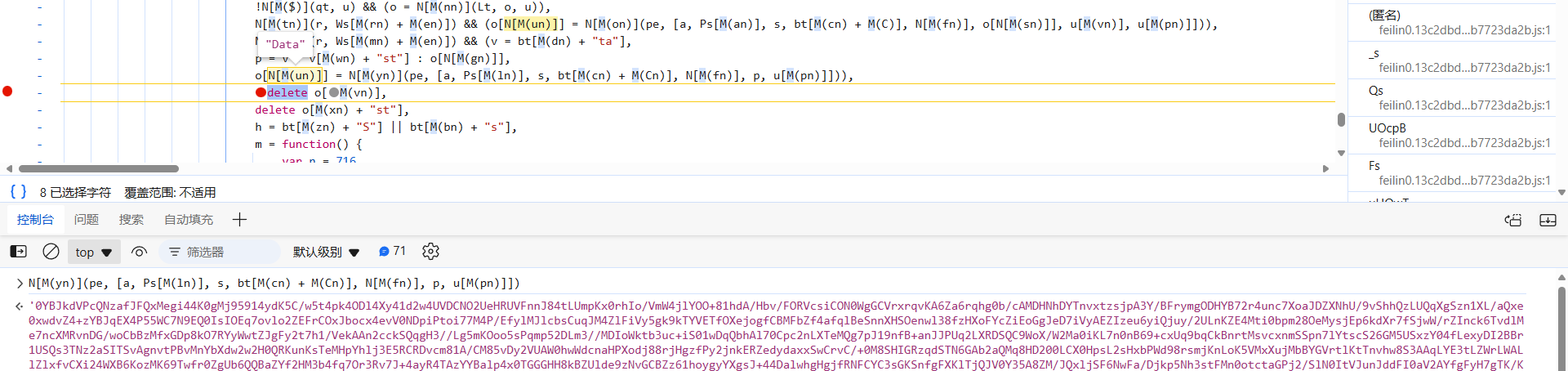
第一次的 Type 为 501,第二次为 combat,u["Data"] 算法走的分支不一样:
往上跟栈就能找到加密位置,第一次校验了一些环境,第二次校验的轨迹:
验证接口的相关加密参数都是在 sg.cdec2e19d71dad5d9c4c.js 文件中生成。
deviceToken、data
最后的验证接口,别的都与之前的类似,主要有两个参数 deviceToken 和 data。同样,跟栈找一下参数值生成的位置:
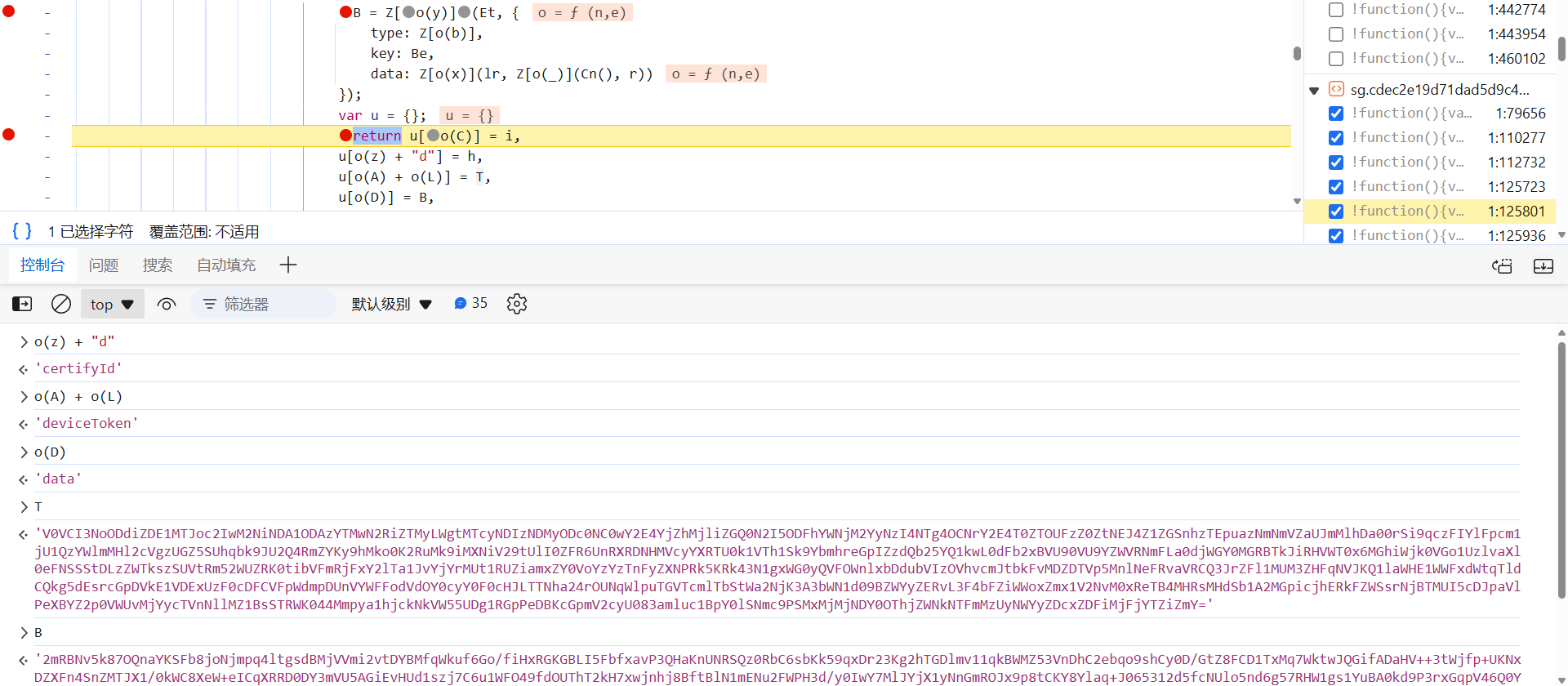
deviceToken 就是 T 参数的值,T 定义在 case 0 中,T = Z[o(w)](ie),return 处下断点,断住后跟到 ie 中去,a 就是 deviceToken 参数的值,继续往 window.um[o(t)] 中跟,分支别走错了:
再跟到 YS 函数中去,看看是如何加密的。进去后会发现,同样的 switch 语句,按 0|1|7|5|4|3|6|2 的顺序执行,也是在加密环境相关的参数:
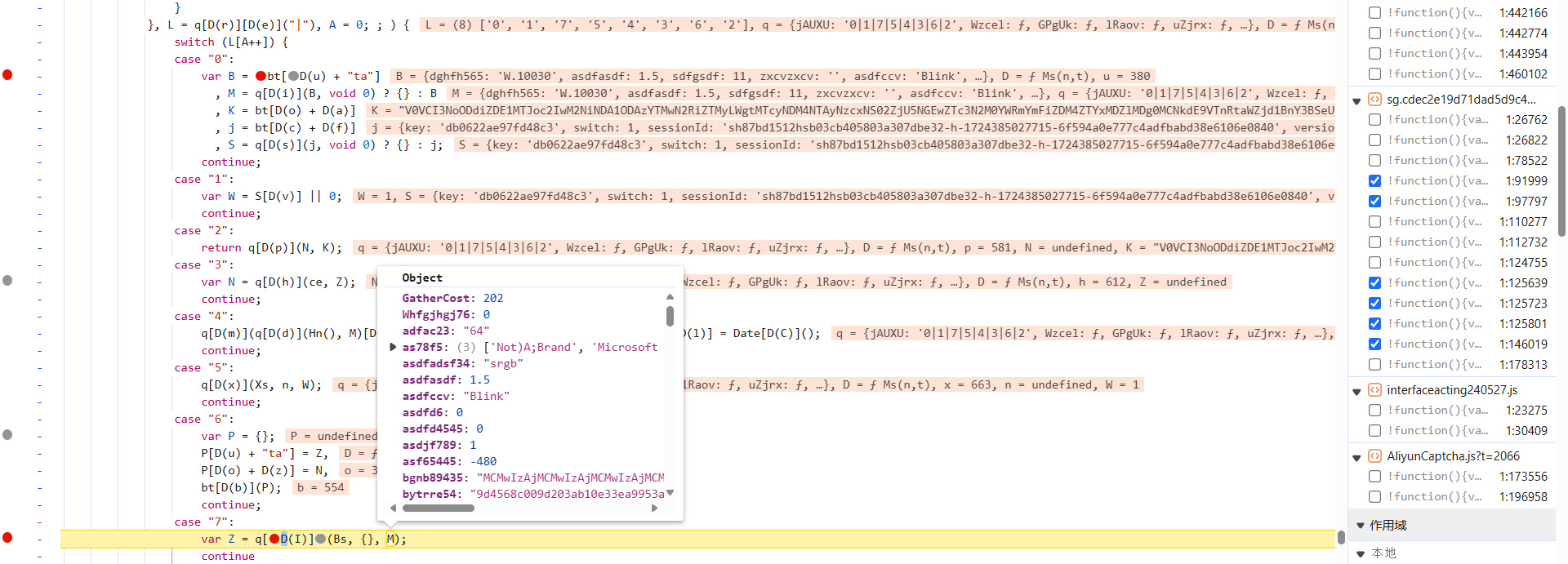
如下图所示,case 6 时,deviceToken 开始被赋值,也就是 N,N 生成在 case 3 处,最后再跟到 ce 函数中去:
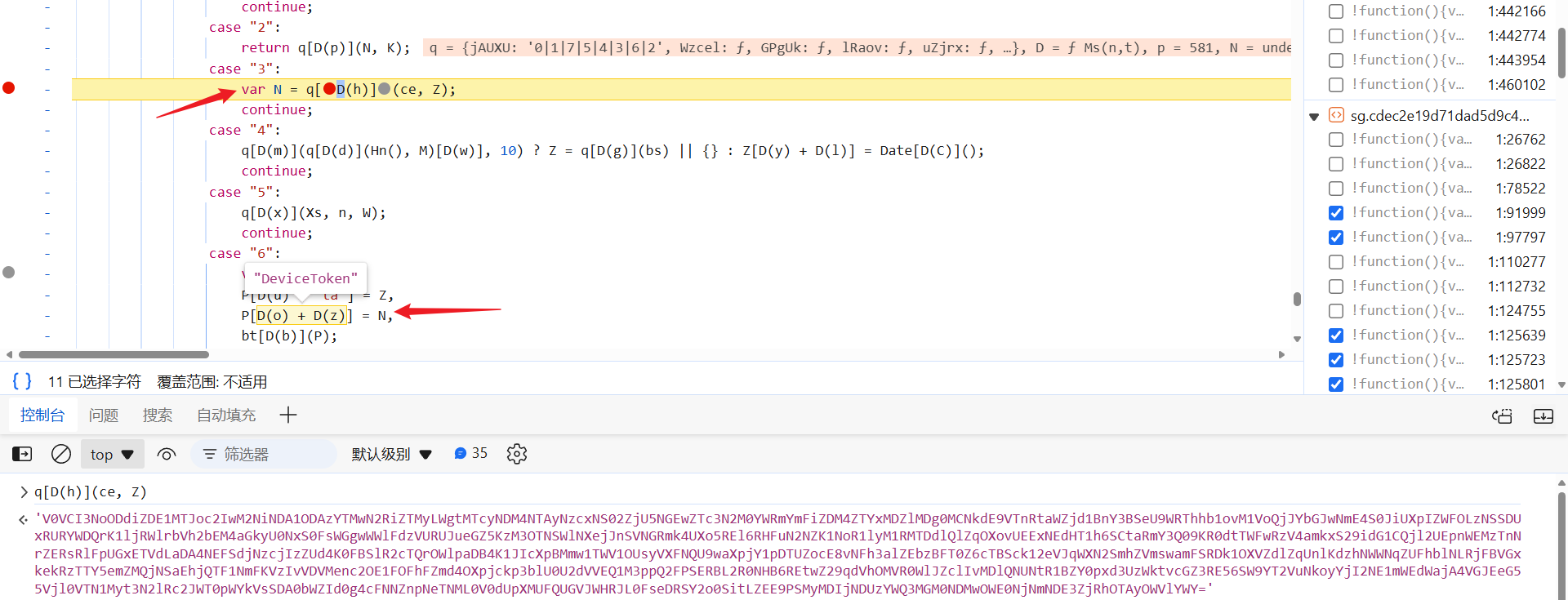
熟悉的配方,熟悉的味道,还是 switch,这个自己跟一下就行了,大差不差,网上的经典图之一,就出自这里:


data 就是对轨迹进行加密处理,其生成位置就在 deviceToken 的下面,也就是 B,一样是 AES 加密。这里的 key 是经过 AES 解密后得到的,为定值,感兴趣的可以去跟一下:
B = Z[o(y)](Et, {
type: Z[o(b)],
key: Be,
data: Z[o(x)](lr, Z[o(_)](Cn(), r))
});
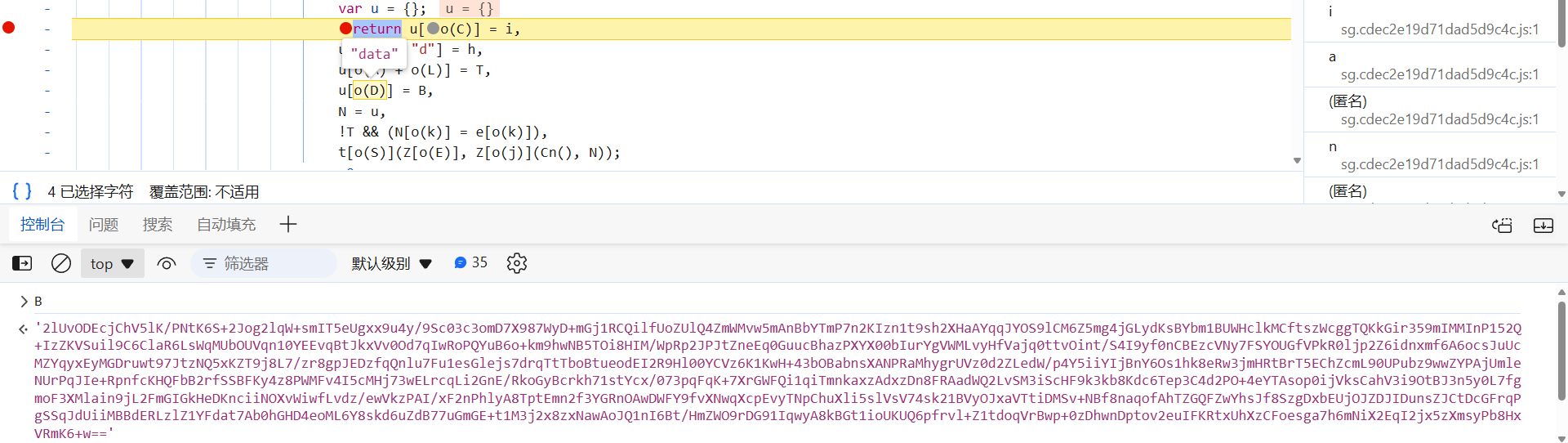
主要来看 B 中的 data,也是经过加密的参数,一层套一层,r 就是经过处理后的轨迹:
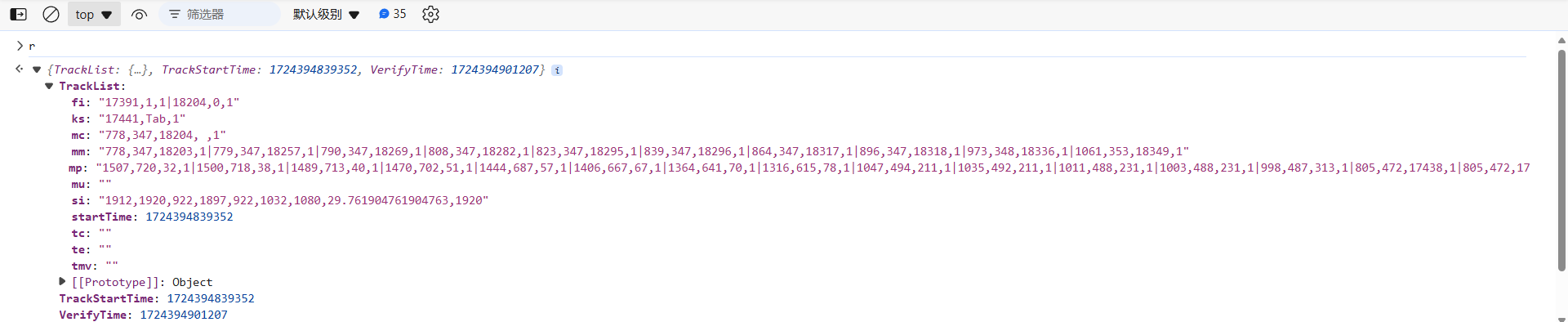
TrackList、TrackStartTime、VerifyTime 在下图处生成,xi 就是原始的轨迹,转换方式并不复杂,可以考虑自写:
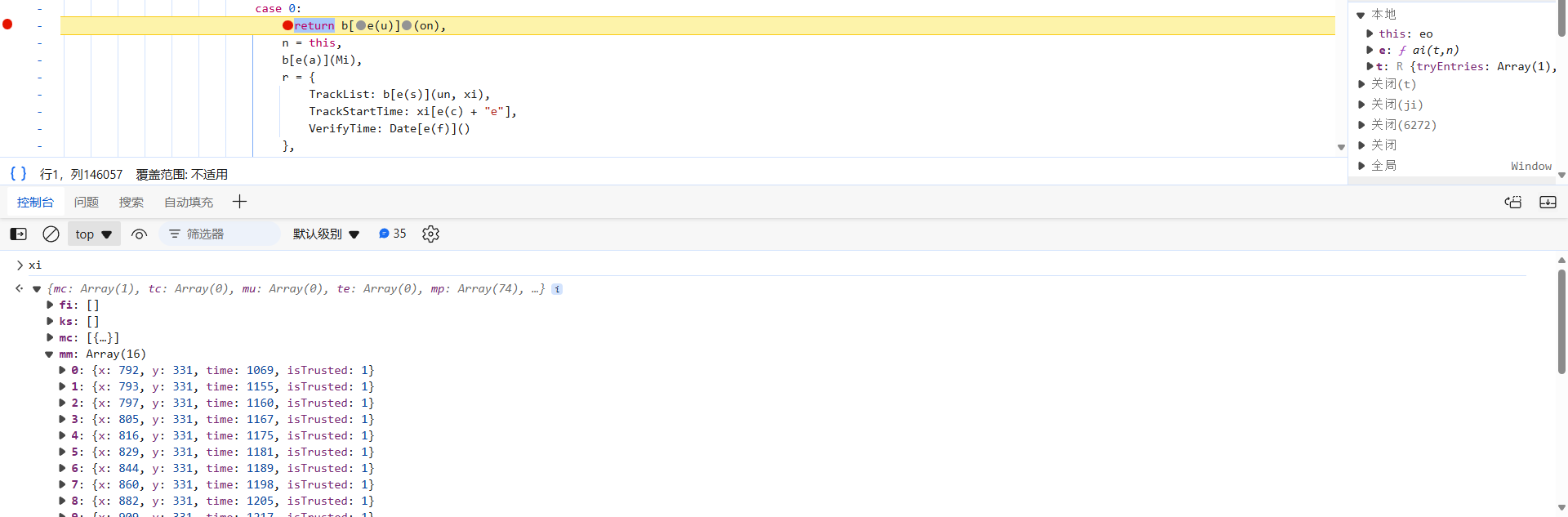
data: Z[o(x)](lr, Z[o(_)](Cn(), r)),后面的部分就是将轨迹对象转换成字符串的形式,主要跟进到 lr 函数中去看看。首先,通过 fr 函数中的 TextEncoder 方法,将轨迹字符串转换成了 UTF-8 编码的二进制数据:
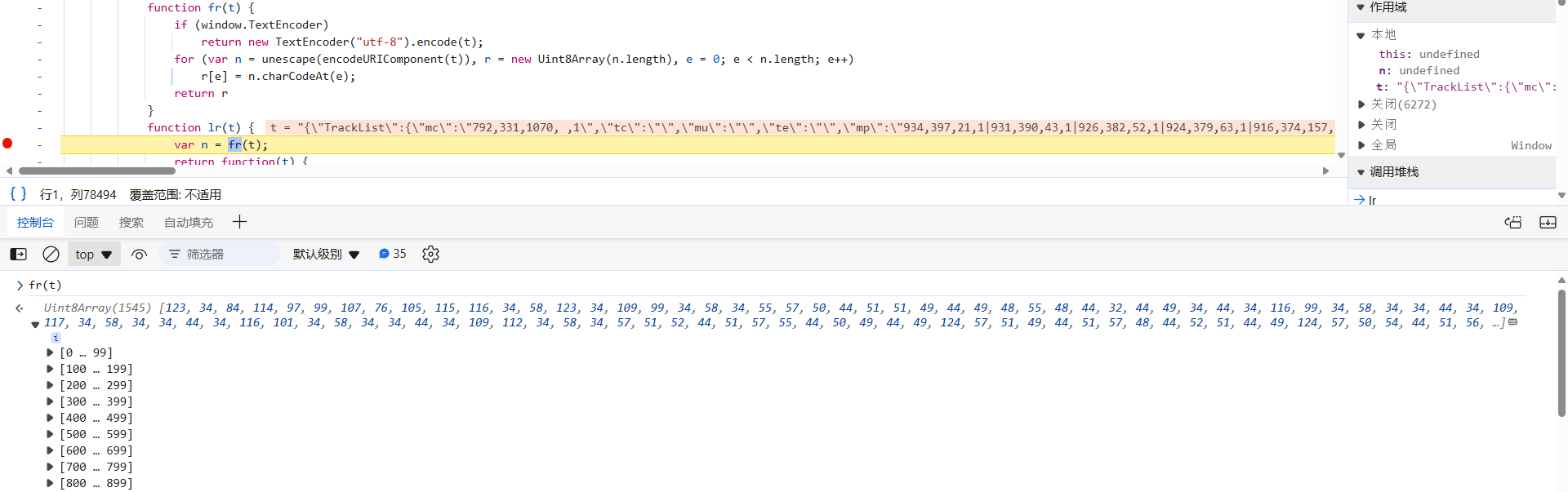
再往下看,return 处是个自执行函数,将二进制数据转换为经过 Base64 编码的字符串。通常都会将二进制数据压缩之后再转换,(0, Un.deflate)(n) 干的就是这活,Deflate 是一种无损数据压缩算法,zlib 格式的数据,用 zlib 模块(C 语言编写)或者 pako 库(JavaScript 编写)实现都可以。至此,算法部分就分析完毕了。
sg 动态研究
经过持续一段时间观察,我们发现 sg 版本也是动态变化的,反复横跳。从最开始的 1.1.0 陆续动态变化到 1.1.10 了,根据注册接口返回的 sg 版本号对应验证接口也需要做动态 Key 的处理,分析方法同上文,可以利用 AST 进行动态 key 的匹配,或者可以去整体分析 sg 代码结构,将他加密函数导出,进行调用直接一步到位生成对应的加密参数。
虽说 sg 是变化的,但是在初始化的时候,通过 AliyunCaptcha.js 注册了很多方法, 配置和动态加载 JavaScript 资源,如下图:
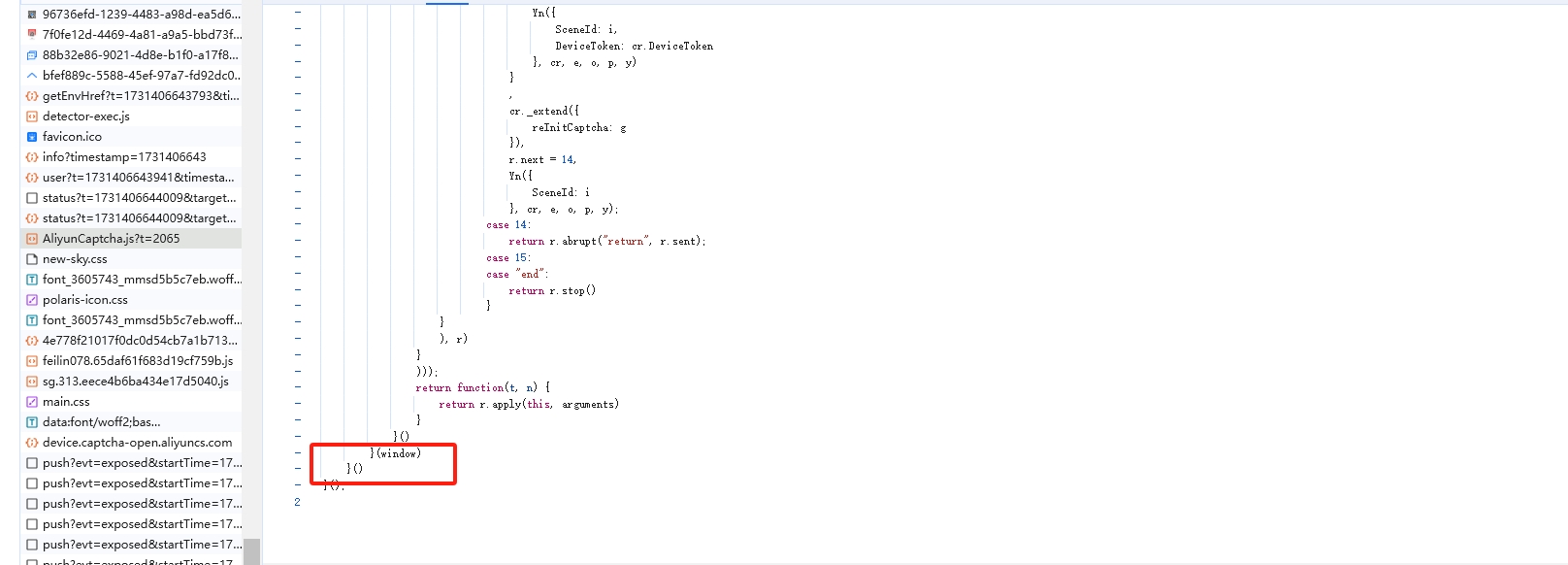
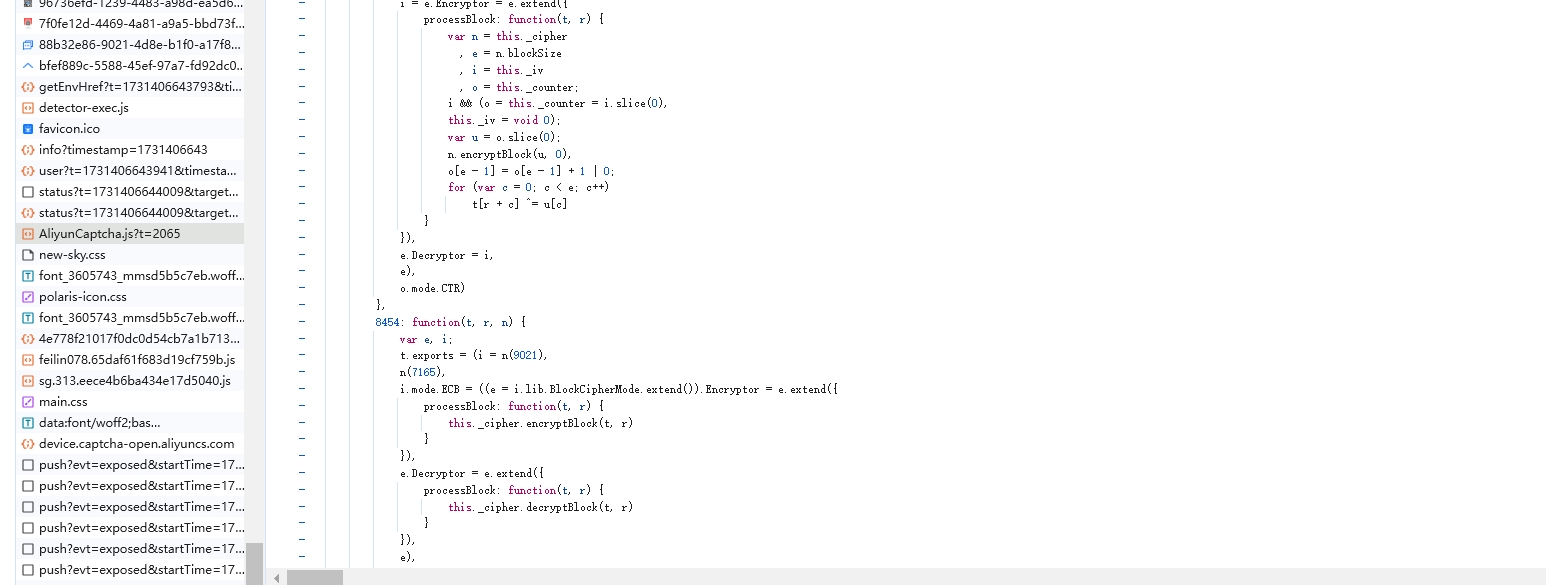
我们同样将 js 拉下来一份,通过补环境的方法在本地将这个模块完全跑通。
按上文思路,我们来找到验证滑块数据包加密参数的位置,如下:
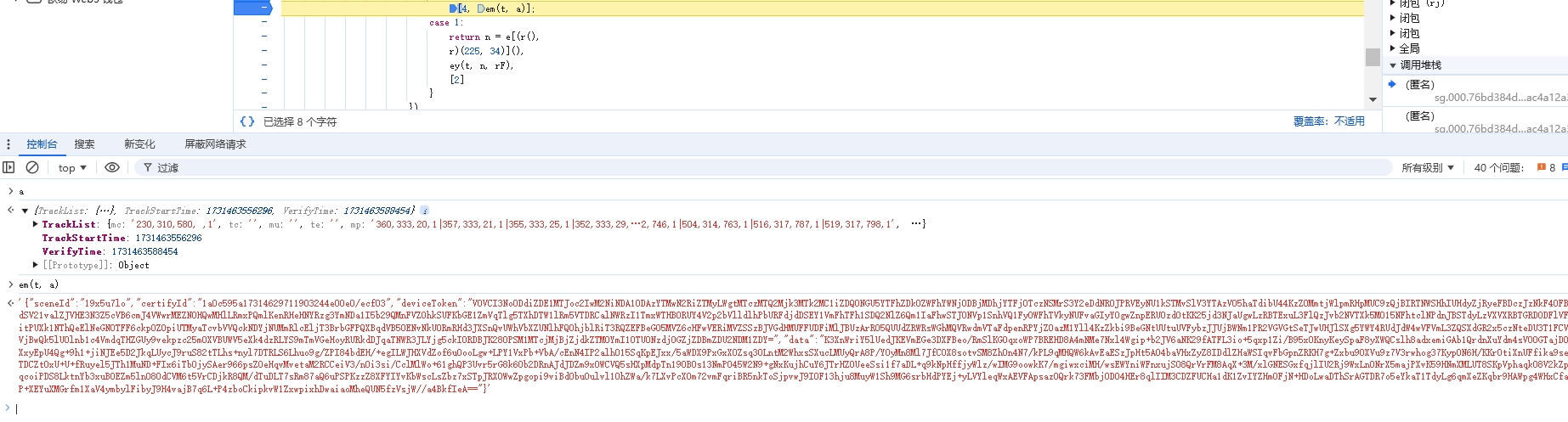
通过 em 函数传入轨迹生成最终的加密字典,该函数传入了 t 函数(ia 函数) 与 轨迹明文,分析可得:

ia 函数最终赋值给了 window.AliyunCaptcha,所以只需将 ia 以及其原型链补齐,即可完成 t 的复现:
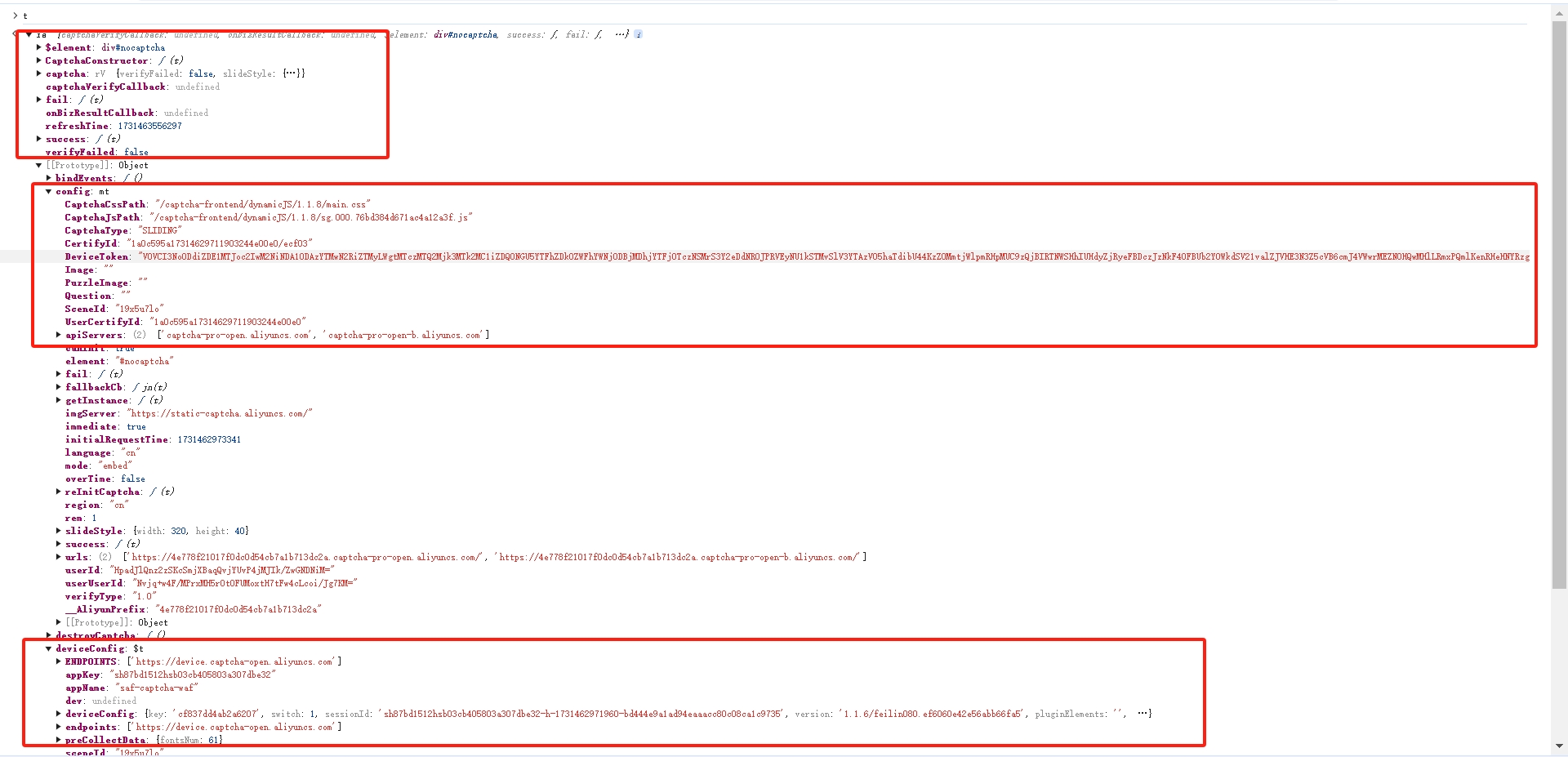
这些原型链里面包括验证出现数据包函数的信息以及滑块注册接口解密返回的 key 信息,userUserId 等等。然后将加密函数 em 导出给 window,调用复现即可:
// AliyunCaptcha.js
// sg.js
window.AliyunCaptcha.prototype = {
"config": config,
"deviceConfig": deviceConfig
}
var t = {
"$element": {},
"onBizResultCallback": undefined,
"verifyFailed": false,
"captcha": {
"verifyFailed": false,
"slideStyle": {
"width": 300,
"height": 40
}
}
}
t.__proto__ = window.AliyunCaptcha.prototype
window.encrypt_(t, track_data)
高版本轨迹区分
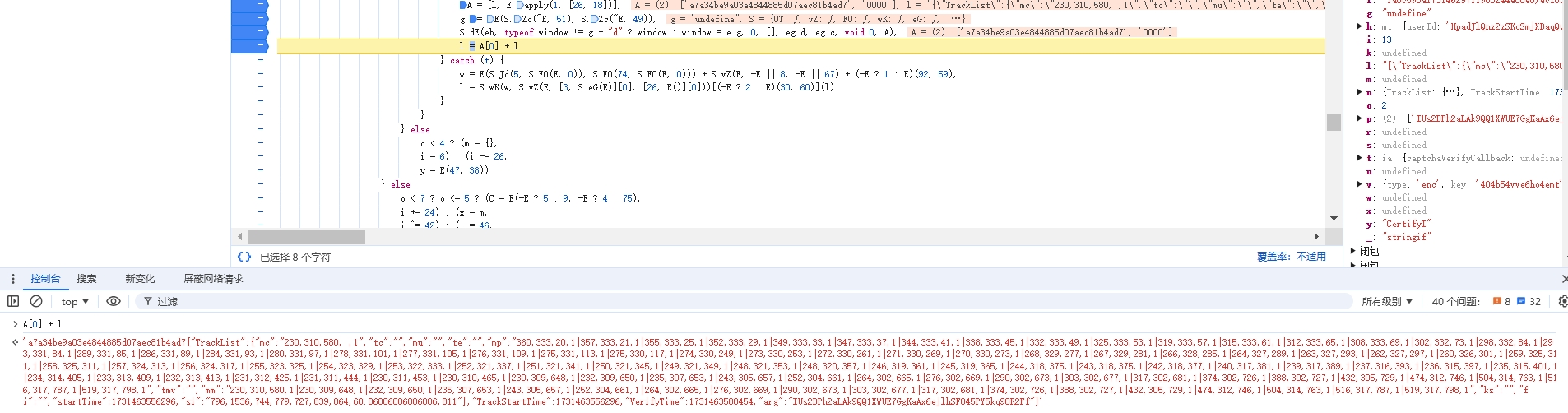
对于较高版本,在单独生成轨迹 data 密文时,传入的参数发生了变化,在前面会多一段哈希值,生成位置如下:

经过该函数通过栈操作和递归即可修改 A[0] 属性值,最终拼接完成轨迹新构造:
S.dE(eb, typeof window != g + "d" ? window : window = e.g, 0, [], eg.d, eg.c, void 0, A),
l = A[0] + l
只需将 eb 函数扣下复现即可:
结果验证
1.1.8
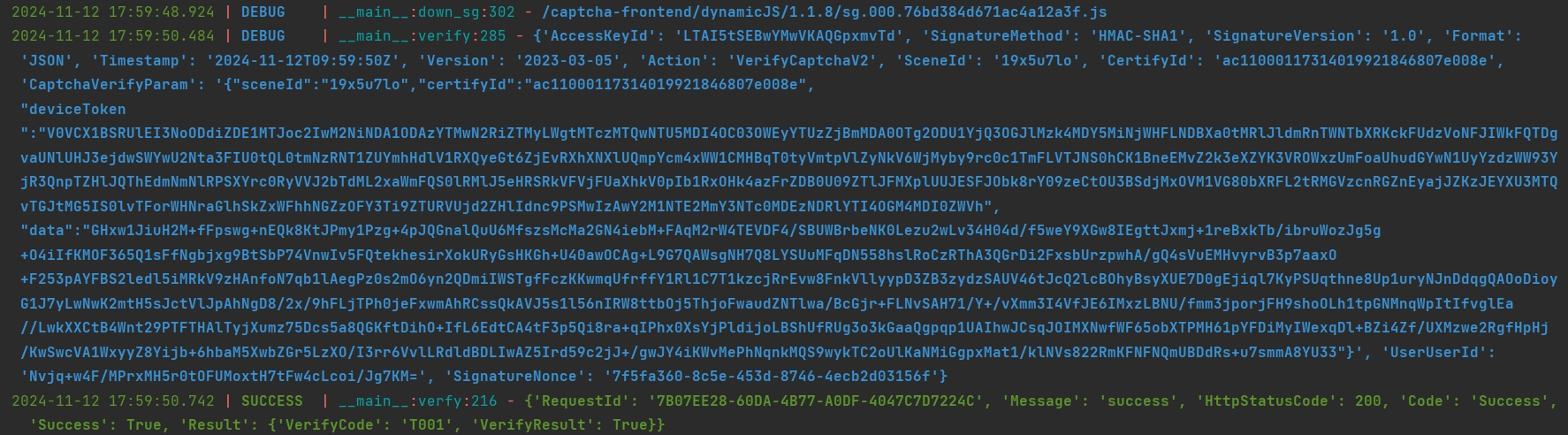
1.1.10