一、前言
平常使用jmeter进行性能测试时,工具自带的监控方式无法清晰直观的查看结果,给我们性能测试带来很多不便。因此我们需要搭建一个可视化性能测试监控平台来实时监控性能测试结果,这里我们采用JMeter+Influxdb+Grafana开源免费框架来实现。
二、实现原理
通过influxdb数据库存储jmeter运行的结果,再通过grafana服务器采集influxdb数据库存储的测试数据,同时通过grafana dashboard展示测试运行结果,完成对jmeter测试结果的平台监控。

三、框架搭建
1. 版本声明
| 组件名称 | 版本说明 |
| 服务器 | win10 64位 |
| Apache jmeter | 5.6.3 |
| JDK | 1.8 |
| InfluxDB | 1.7.9 |
| Grafana | 11.3.1 |
2. InfluxDB下载和安装
官网链接:https://portal.influxdata.com/downloads#influxdb
Windows可使用以下链接直接下载
https://dl.influxdata.com/influxdb/releases/influxdb-1.7.9_windows_amd64.zip
我这里直接下载的1.7.9的版本,没有用V2版本,老版本相对来说比较稳定。而且V2版本当中没有influx.exe客户端文件,需要下载类似于InfluxDBStudio软件来操作数据库。老版本自带influx.exe客户端文件,可以cmd窗口直接打开进行SQL命令输入等操作。
下载完成后进行解压,以Windows为例:
①.进入文件夹可看到以下目录下载完成后进行解压,以Windows为例:
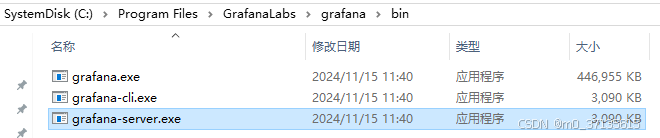
②.点击 influxd.exe启动数据库,启动成功如下图所示:
3. Grafana下载和安装
首先进入grafana官网下载安装包
Download Grafana | Grafana Labs
选择对应系统后下载,以Windows为例:
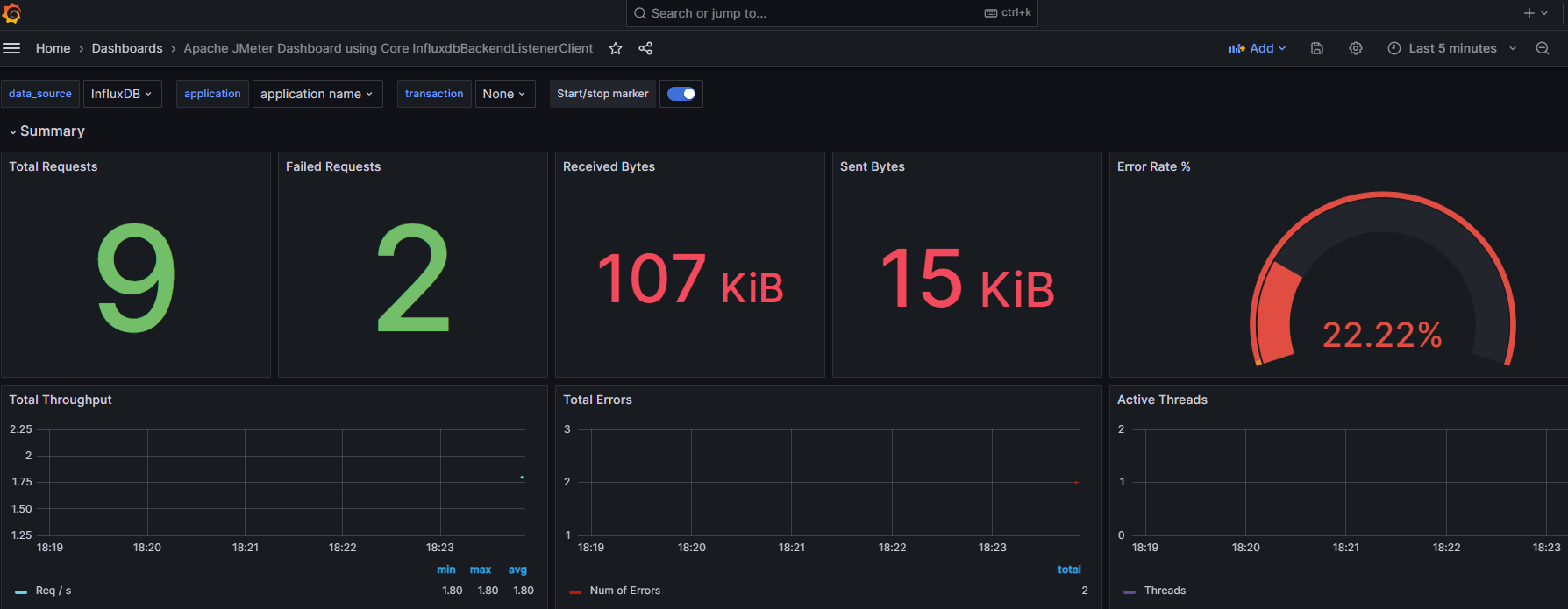
①.解压完成后进入bin目录点击grafana-server.exe 来启动 Grafana 程序
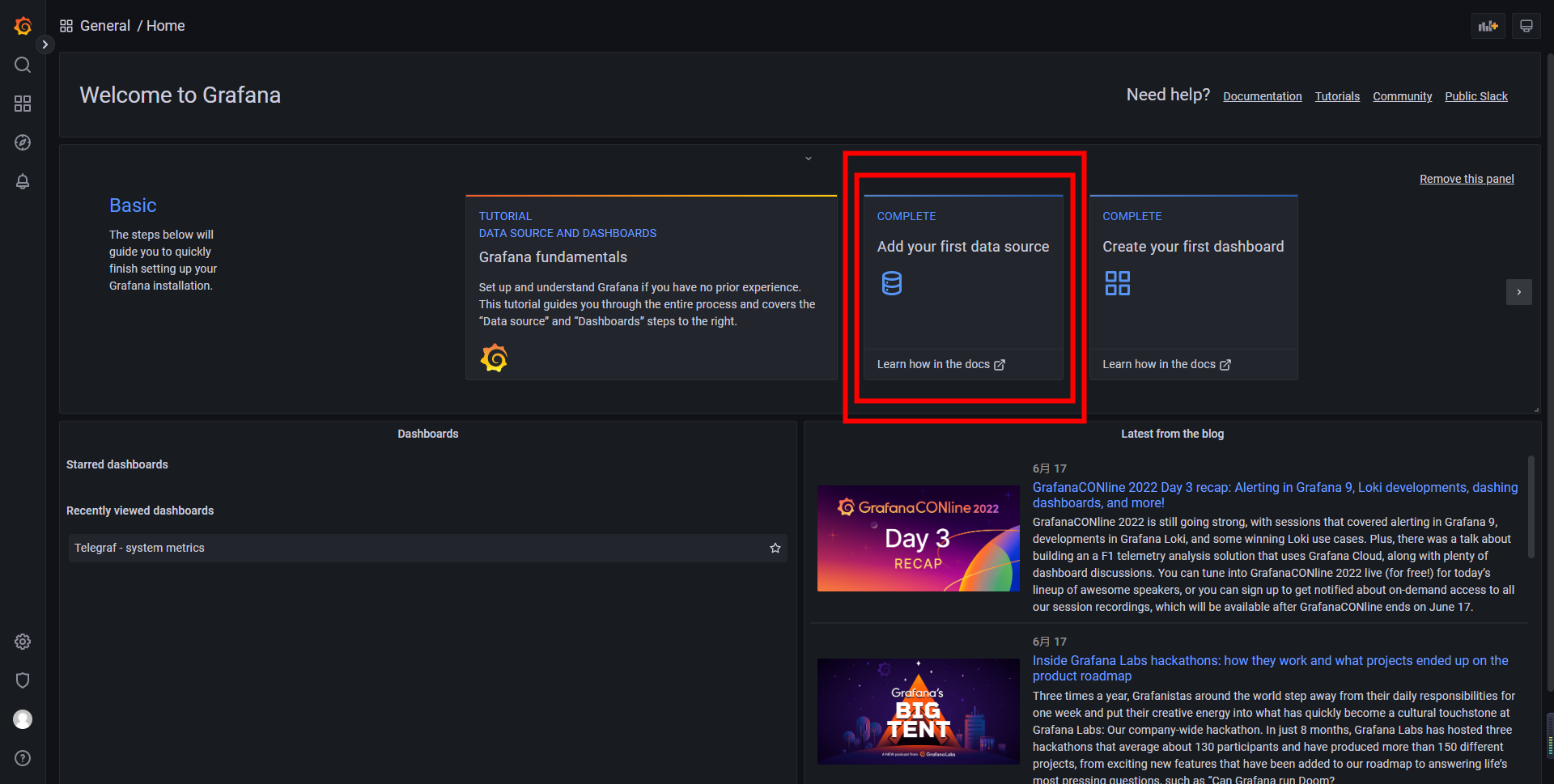
②.启动完成后打开浏览器输入http://localhost:3000 进入 Grafana 登录页面,默认用户名和密码都为admin
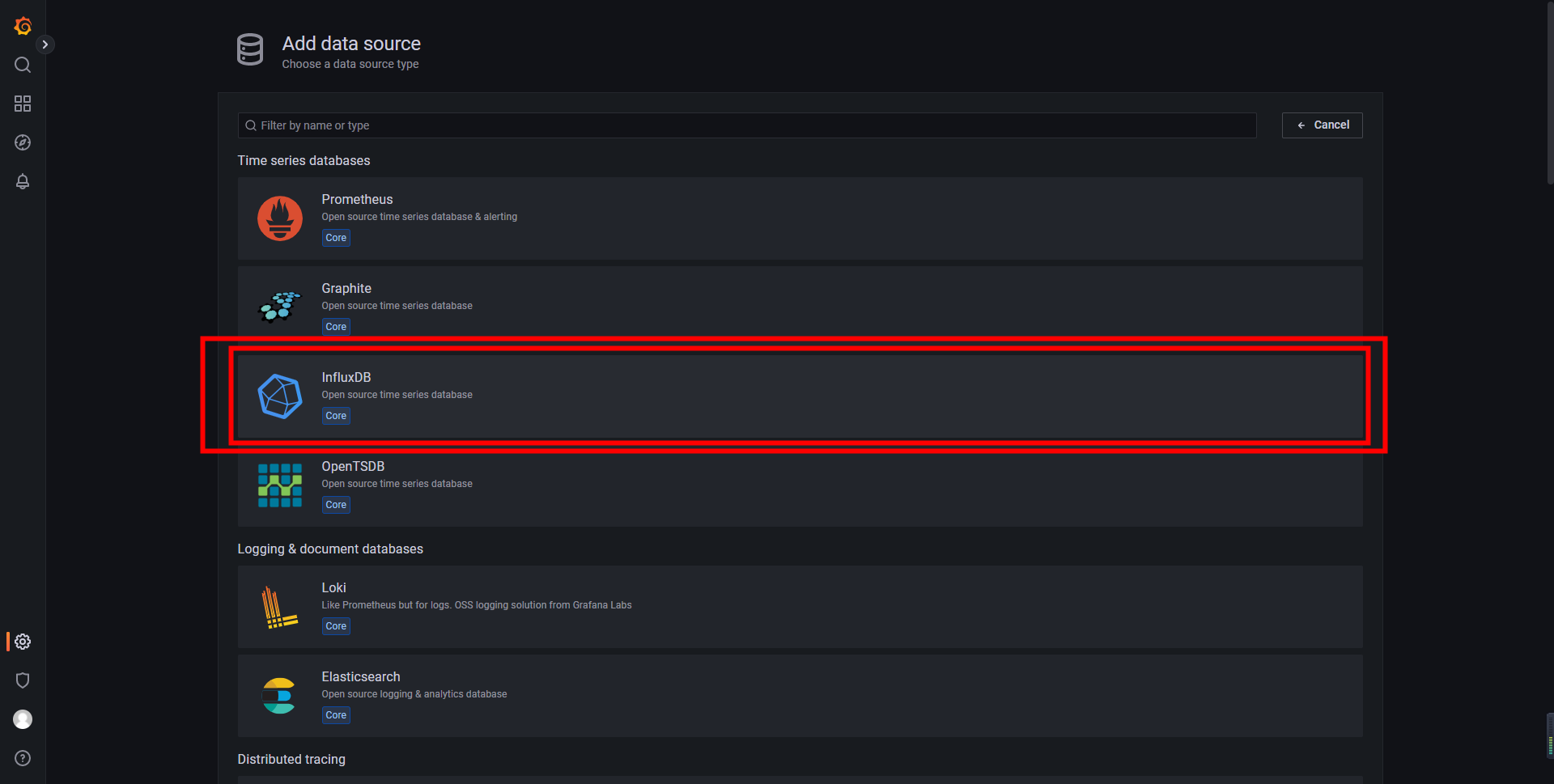
③.进入首页后点击添加数据库
选择 Influxdb 数据库
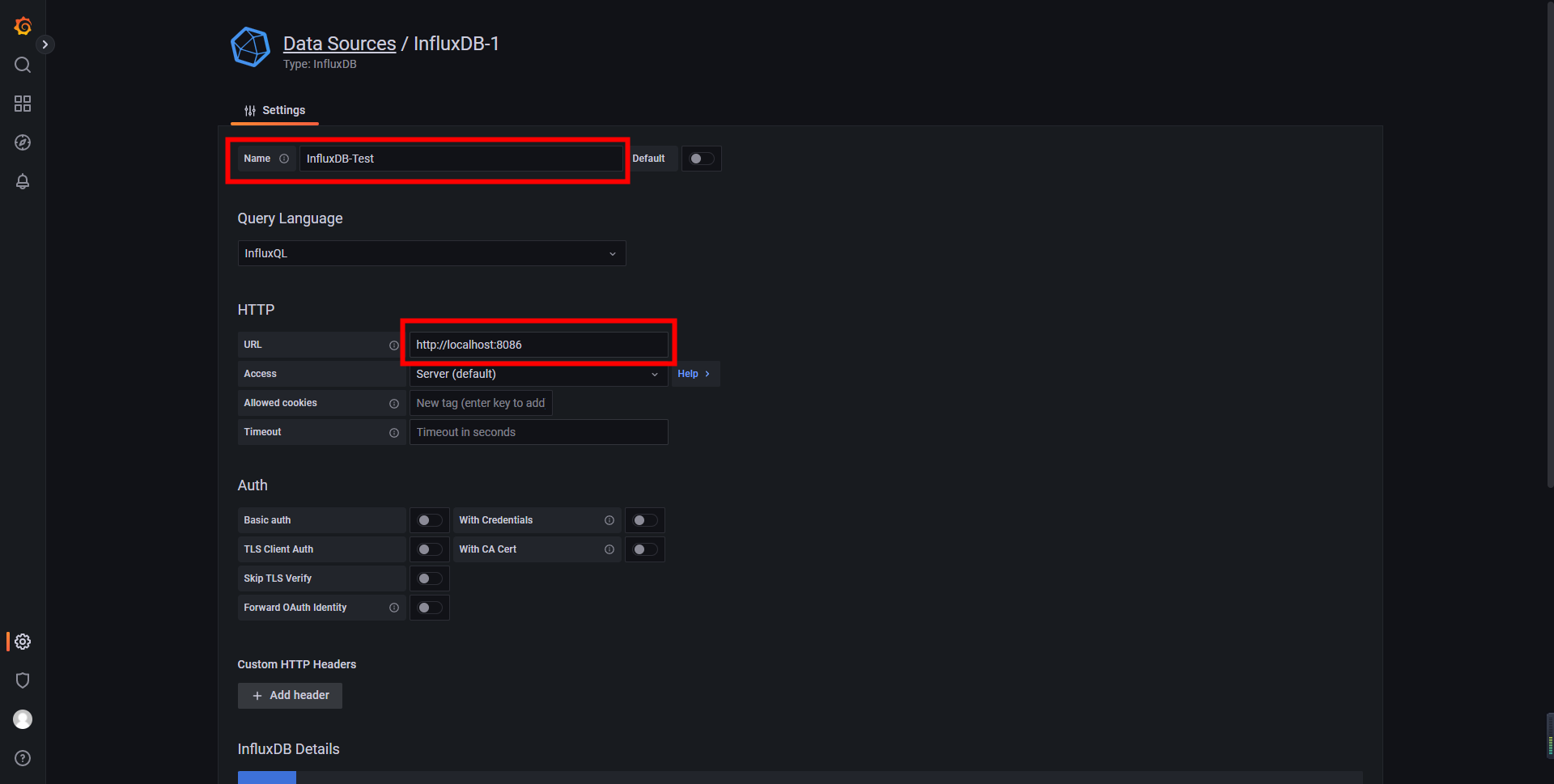
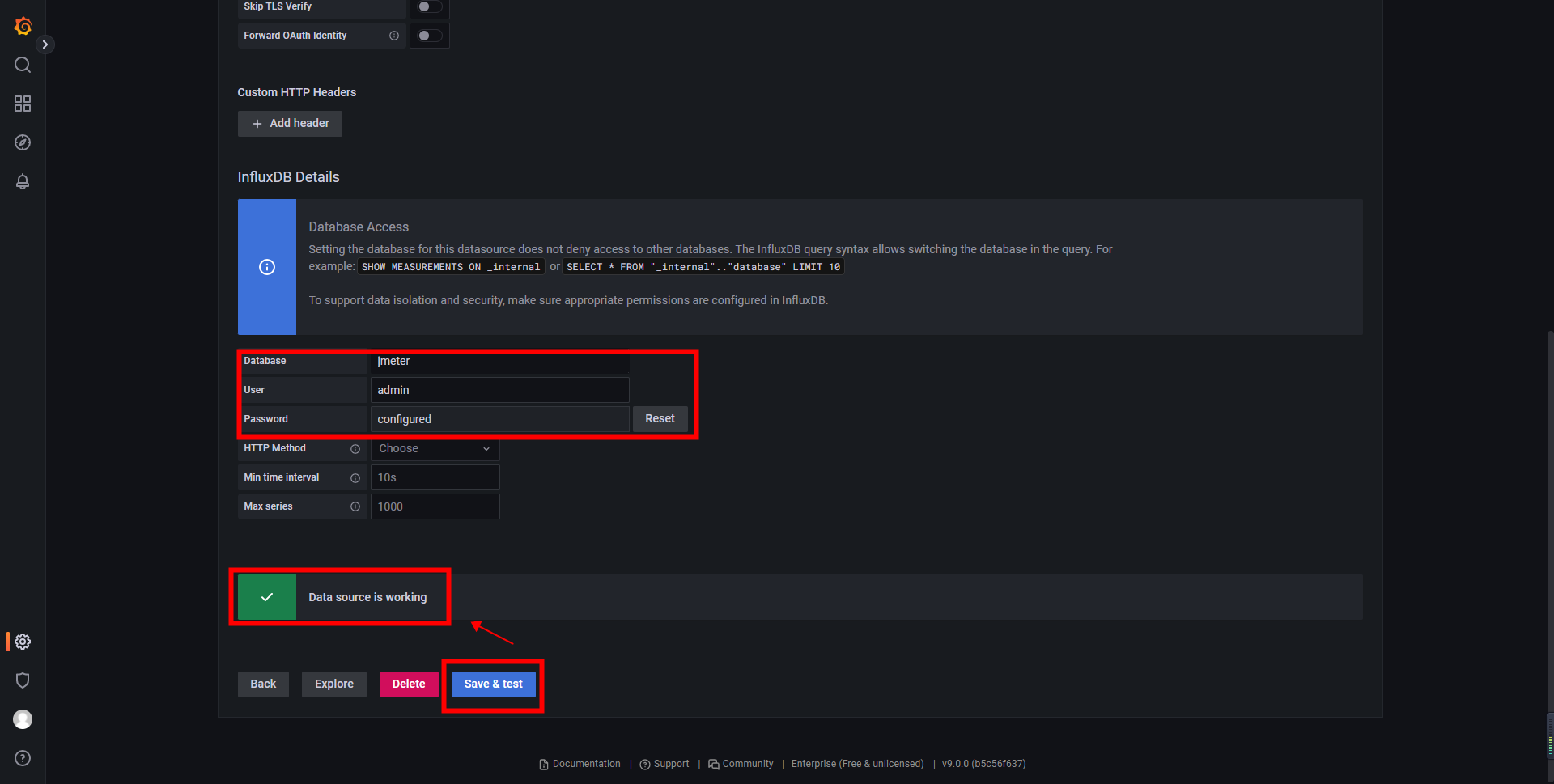
填写以下信息即可
点击 Sava&test,显示 data source is working 表示数据库连接成功
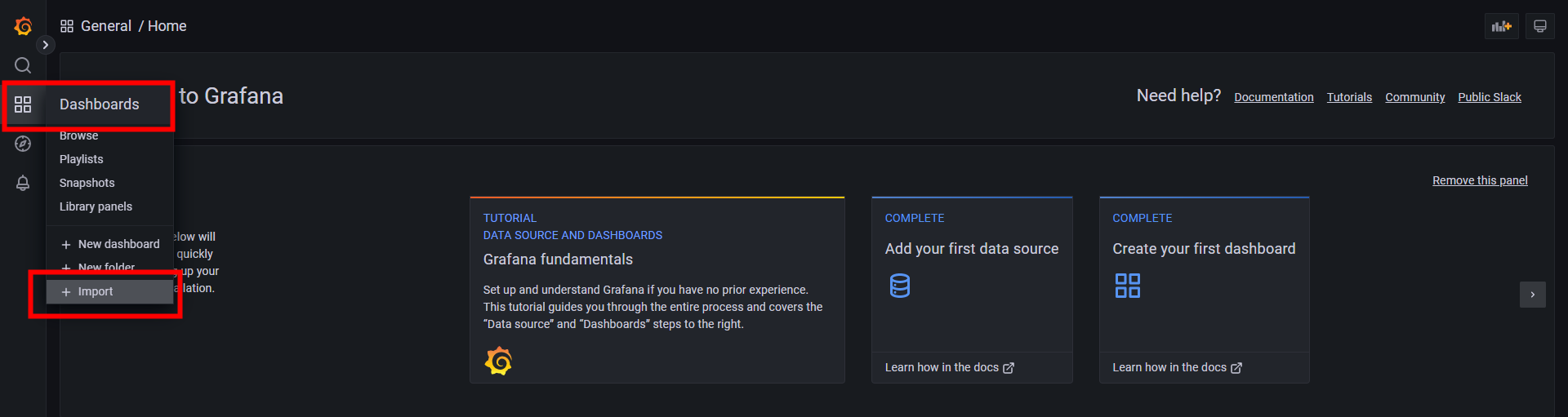
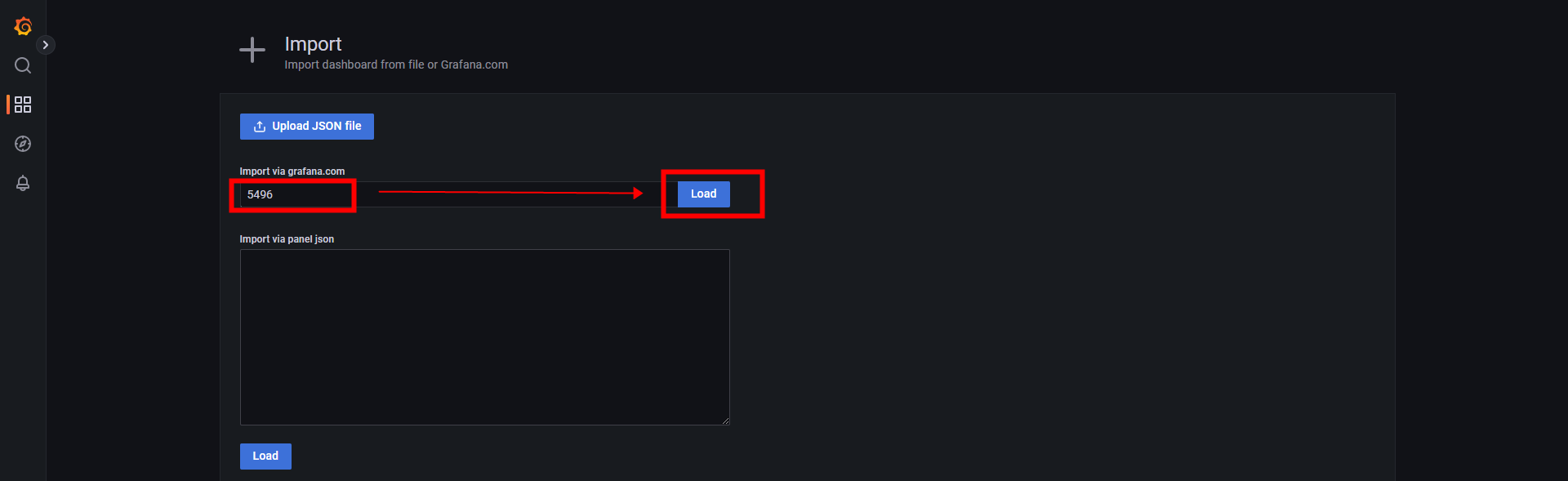
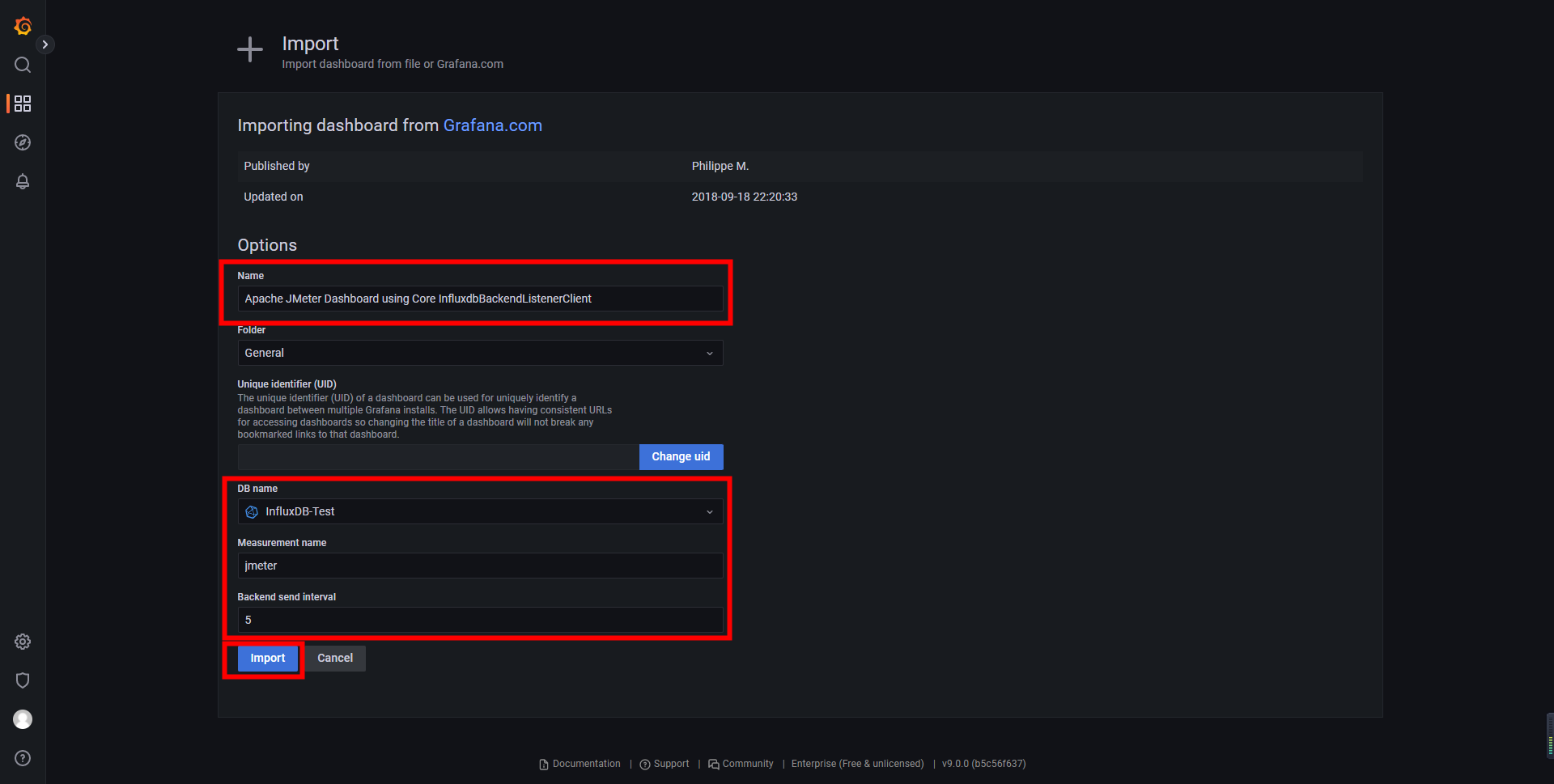
④.导入仪表盘import dashboard(注:JMeter:5496 Telegraf:5955)
添加完成后效果如下:
可以到 Grafana 官网 (https://grafana.com/grafana/dashboards)寻找模板,在导入模板处输入需要模板的Downlosds编号即可
4. JMeter配置
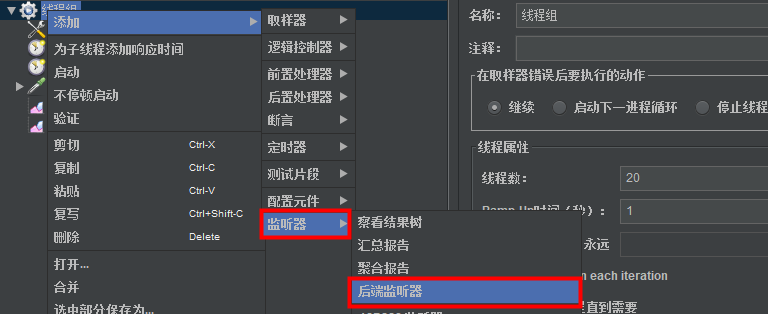
①. JMeter 中,导入测试脚本后,在线程组当中添加“监听器 -> 后端监听器”
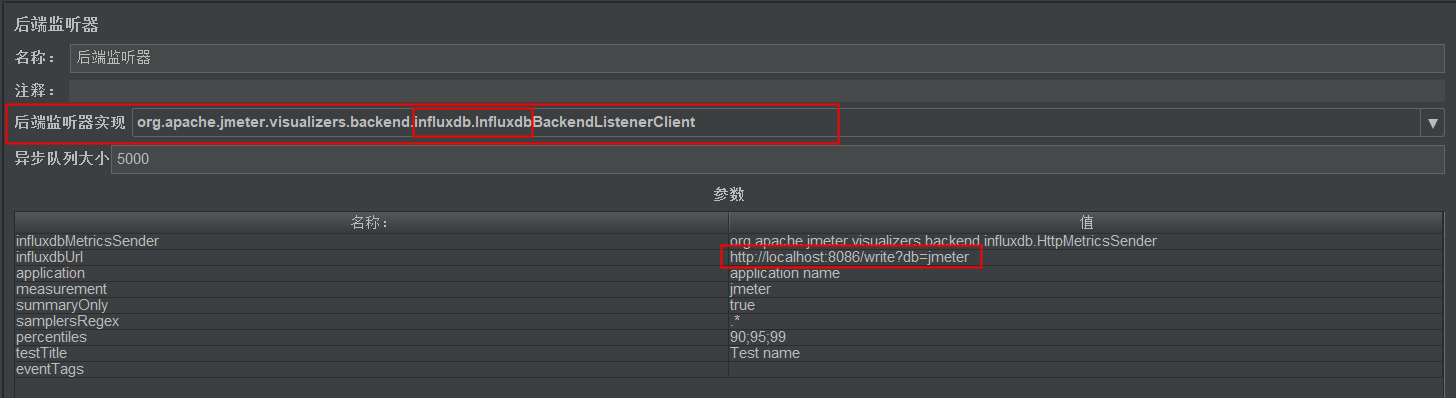
②.配置后端监听器
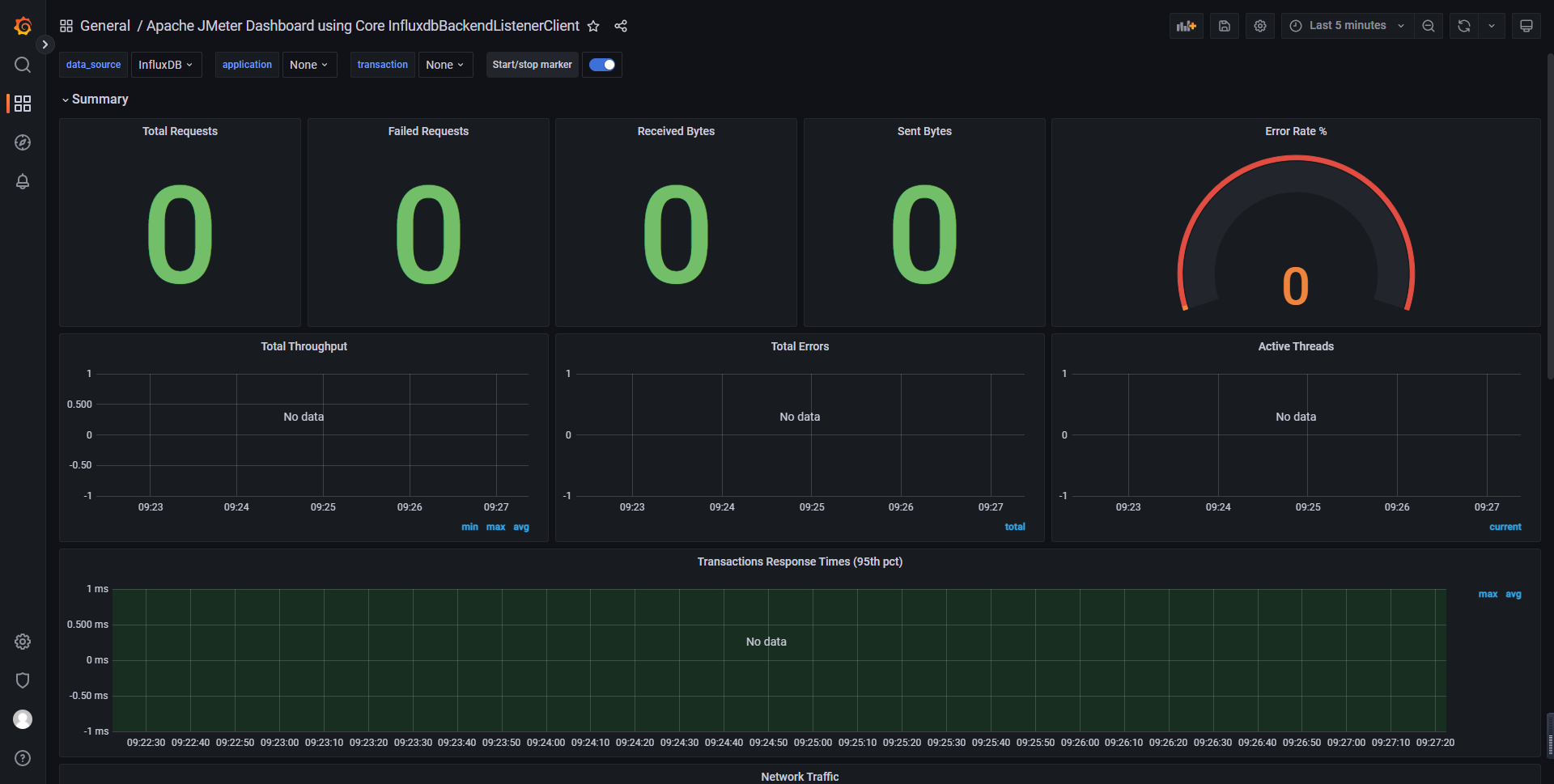
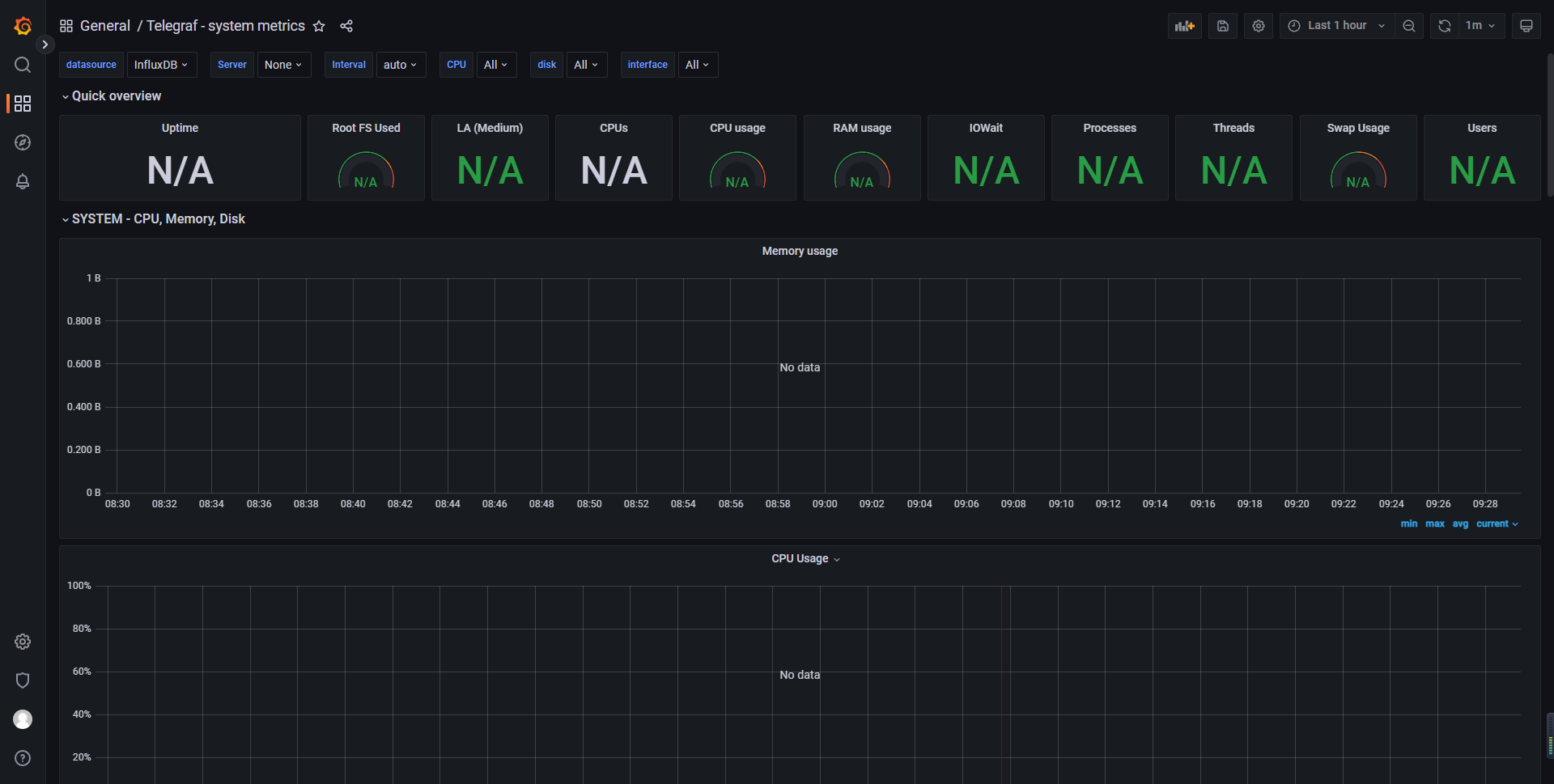
5. 运行效果
四、避坑秘籍
在搭建Jmeter+influxdb+grafana框架过程中踩了下面几个坑,放在这里提醒大家注意哈:
1. jmeter配置代理服务器
主要是由于我司连接外网都需要经过代理服务器,如果大家公司没有用代理服务器,那此处可忽略,不需要关注哈
解决方案:在安装的jmeter/bin目录下新建一个文件jmeterWithProxy.bat,打开输入如下命令保存
命令:jmeter.bat -H 代理服务器域名 -P 8080 -u 用户名 -a 密码
第一次运行jmeter脚本发送京东商城登录请求时,发现一直连接超时,公司代理服务器搞的鬼,后来通过抓包解决。
2. Influxdb未新建jmeter数据库
刚开始一步步下载安装以及打开grafana服务器,结果发现没有数据在dashboard显示。这个折腾了好久,刚开始以为grafana服务器连接后会自动创建数据库,因为在服务器上面有配置数据库名称jmeter,这里我自己以为了,结果可想而知咯。
解决方案:在cmd 窗口进入到启动influxdb-1.7.9-1\influx.exe下面, 启动数据库客户端并输入如下命令就行(记得最后加上分号运行)
create database jmeter;
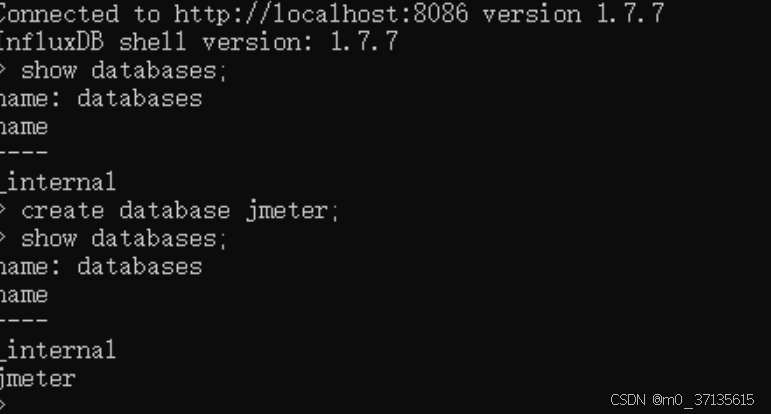
3. 未修改influxdb.conf文件
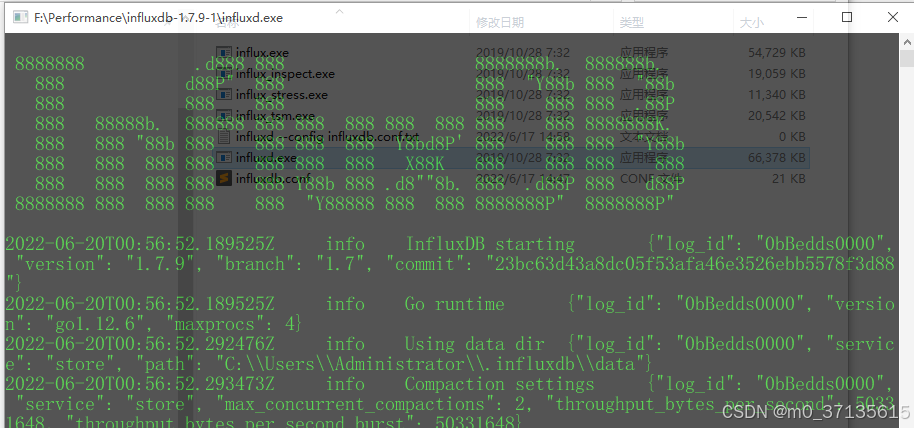
influxdb.conf这个文件很重要,influxd.exe服务器第一次启动之后会生成如下几个文件,后面我们会把jmeter产生的报告存储到该路径的数据库里面,所以要提前做好配置,默认配置应该是linux的路径,这个坑整死人,挣扎了好久才搞清楚。
解决方案:
① 修改 influxdb.conf 本地配置文件(修改数据存储路径)
② 修改完成后点击 influxd.exe(使用配置文件启动,需切换到该目录,执行 influxd --config influxdb.conf )再次启动数据库
标签:jmeter,Grafana,性能,influxdb,grafana,exe,测试,JMeter,数据库 From: https://blog.csdn.net/m0_37135615/article/details/144076302最后在这里啰嗦几句,整理文档不易,一个多月整理了二十多份文档,以前总感觉知识太零散,我也从这次复习总结当中学习了更多。大家可以多留言交流,或者文档中有错误请帮忙指正。“三人行,必有我师焉”,希望有更多同行人一起加入学习,升职加薪,不枉我日夜加班整理文档共享给大家,分享万岁,同行万岁!