对于每一个点 \(u\),我们先找到满足右述条件的深度最小的 \(u\) 祖先 \(f\) 并记这个深度最小的祖先的深度为 \(dp(u)\):\(f\) 能只通过除了树上 \([f,u]\) 路径所包含的边之外的边到达 \(u\)。
那么显然,一次询问 \([a,b]\) 中,对于 \(b\) 的子树中的一点 \(u\),\(1\) 号点能到达 \(u\) 当且仅当 \(\min\limits_{v\in[b,u]} dp(v)\leq dep(a)\)。
我们先看如何把 \(dp(u)\) 给求出来。
我们枚举满足条件的深度最小的祖先 \(f\) 最后一步是通过哪一个点到达 \(u\) 的,也就是枚举所有指向 \(u\) 的且的非树边,设这条边为 \((v,u)\):
-
若 \((v,u)\) 为后向边,那么 \(v\) 为 \(u\) 的祖先,那么 \(v\) 的上一步仍不能是树边,于是更新:\(dp(u)\gets\min(dp(u),dp(v))\)。
-
若 \((v,u)\) 为横叉边,设 \(v,u\) 的最近公共祖先为 \(lca\):
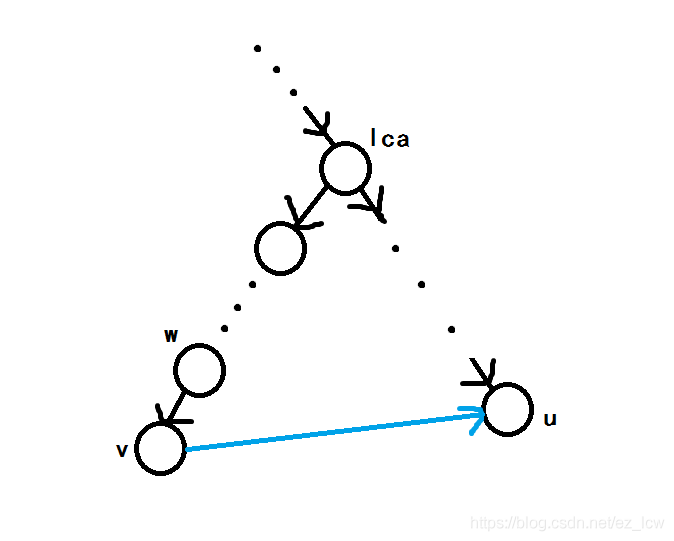
我们考虑枚举 \(v\) 的上一步是沿树边从哪里走到了 \(v\):对于树上 \([lca,v]\) 路径上的任意一点 \(w\),我们都可以更新:\(dp(u)\gets \min(dp(u),dp(w))\)。
这样更新是正确的,因为 \(dp(w)\) 要求不经过树上 \([f,w]\) 路径上的边,那么也就不经过树上 \([f,lca]\) 路径上的边,同时由于这是一棵 dfs 树,既然存在了边 \((v,u)\),也就不存在 \((lca,u]\) 中某一点指向 \((lca,v]\) 中某一点的边,所以这条从 \(f\) 到达 \(w\) 的路径也不会经过 \((lca,u]\)。
这样更新显然也是充分的,我们充分地枚举了 \(v\) 的上一步沿树边走是从哪里走到 \(v\)。
于是我们考虑拓扑排序进行 DP,至于横叉边转移中的 \(\min\limits_{w\in[lca,v]}dp(w)\) 如何求,我们用倍增即可,因为这里没有修改。我们只需要在拓扑排序中更新完 \(dp(u)\) 时把 \(u\) 往上的倍增数组求出来。
回到询问,现在的问题是多次询问 \([a,b]\),询问 \(b\) 的子树中有多少个点 \(v\) 满足 \(\min\limits_{v\in[b,u]} dp(v)\leq dep(a)\)。
考虑离线,并对 \(b\) 跑线段树合并:
我们在原树上 dfs,并对于每一个当前点 \(b\) 维护这么一棵线段树:下标为 \(i\) 的叶子节点中存储着 \(\min\limits_{v\in[b,u]} dp(v)=i\) 的 \(u\) 的个数,也就是 \(\min\limits_{v\in[b,u]} dp(v)\) 的值域线段树。
然后回溯时合并儿子的线段树再用当前点的 \(dp\) 值更新即可。
碰到询问时直接查询 \(\min\limits_{v\in[b,u]} dp(v)\leq dep(a)\) 的 \(u\) 的个数即可。
#include<bits/stdc++.h>
#define LN 17
#define N 100010
#define INF 0x7fffffff
#define lc(u) ch[u][0]
#define rc(u) ch[u][1]
using namespace std;
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
x=(x<<1)+(x<<3)+(ch^'0');
ch=getchar();
}
return x*f;
}
struct Query
{
int a,id;
Query(){};
Query(int x,int y){a=x,id=y;}
};
int n,m,q;
int du[N];
int cnt,head[N],nxt[N],to[N];
int fa[N][LN],d[N],size[N];
int dp[N],minn[N][LN];
int node,rt[N],ch[N*LN][2],sum[N*LN];
int ans[N];
vector<int>e[N];
vector<Query>p[N];
void adde(int u,int v)
{
to[++cnt]=v;
nxt[cnt]=head[u];
head[u]=cnt;
}
void dfs(int u)
{
size[u]=1;
for(int i=1;i<=16;i++)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(int v:e[u])
{
if(fa[v][0]) continue;
fa[v][0]=u;
d[v]=d[u]+1;
adde(u,v);
dfs(v);
size[u]+=size[v];
}
}
int calc(int a,int b)
{
bool flag=0;
if(d[a]<d[b]) swap(a,b),flag=1;
int ans=INF;
for(int i=16;i>=0;i--)
{
if(d[fa[a][i]]>=d[b])
{
if(!flag) ans=min(ans,minn[a][i]);
a=fa[a][i];
}
}
if(a==b) return min(ans,minn[a][0]);
if(flag) swap(a,b);
for(int i=16;i>=0;i--)
{
if(fa[a][i]!=fa[b][i])
{
ans=min(ans,minn[a][i]);
a=fa[a][i],b=fa[b][i];
}
}
return min(ans,minn[a][1]);
}
void DP()
{
for(int i=1;i<=n;i++) minn[i][0]=d[i];
queue<int>q;
q.push(1);
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=1;i<=16;i++)
minn[u][i]=min(minn[u][i-1],minn[fa[u][i-1]][i-1]);
for(int v:e[u])
{
if(u!=fa[v][0]) minn[v][0]=min(minn[v][0],calc(u,v));
du[v]--;
if(!du[v]) q.push(v);
}
}
}
void up(int u)
{
sum[u]=sum[lc(u)]+sum[rc(u)];
}
void merge(int &a,int b,int l,int r)
{
if(!a)
{
a=b;
return;
}
if(!b) return;
if(l==r)
{
sum[a]+=sum[b];
return;
}
int mid=(l+r)>>1;
merge(lc(a),lc(b),l,mid);
merge(rc(a),rc(b),mid+1,r);
up(a);
}
int query(int u,int l,int r,int ql,int qr)
{
if(!u) return 0;
if(ql<=l&&r<=qr) return sum[u];
int mid=(l+r)>>1,ans=0;
if(ql<=mid) ans+=query(lc(u),l,mid,ql,qr);
if(qr>mid) ans+=query(rc(u),mid+1,r,ql,qr);
return ans;
}
void del(int &u,int l,int r,int ql,int qr)
{
if(!u) return;
if(ql<=l&&r<=qr)
{
u=0;
return;
}
int mid=(l+r)>>1;
if(ql<=mid) del(lc(u),l,mid,ql,qr);
if(qr>mid) del(rc(u),mid+1,r,ql,qr);
up(u);
}
void update(int &u,int l,int r,int x,int v)
{
if(!u) u=++node;
if(l==r)
{
sum[u]+=v;
return;
}
int mid=(l+r)>>1;
if(x<=mid) update(lc(u),l,mid,x,v);
else update(rc(u),mid+1,r,x,v);
up(u);
}
void solve(int u)
{
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
solve(v);
merge(rt[u],rt[v],1,n);
}
int nv=minn[u][0];
int tmp=query(rt[u],1,n,nv+1,n);
del(rt[u],1,n,nv+1,n);
update(rt[u],1,n,nv,tmp+1);
for(Query now:p[u])
ans[now.id]=size[u]-query(rt[u],1,n,1,d[now.a]);
}
int main()
{
n=read(),m=read(),q=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
e[u].push_back(v);
du[v]++;
}
for(int i=1;i<=n;i++)
sort(e[i].begin(),e[i].end());
d[1]=1;
dfs(1);
DP();
for(int i=1;i<=q;i++)
{
int a=read(),b=read();
p[b].push_back(Query(a,i));
}
solve(1);
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
return 0;
}