leetcode78 子集

思路:深度优先搜索回溯
分析此类问题可以先用树形结构模拟代码逻辑。
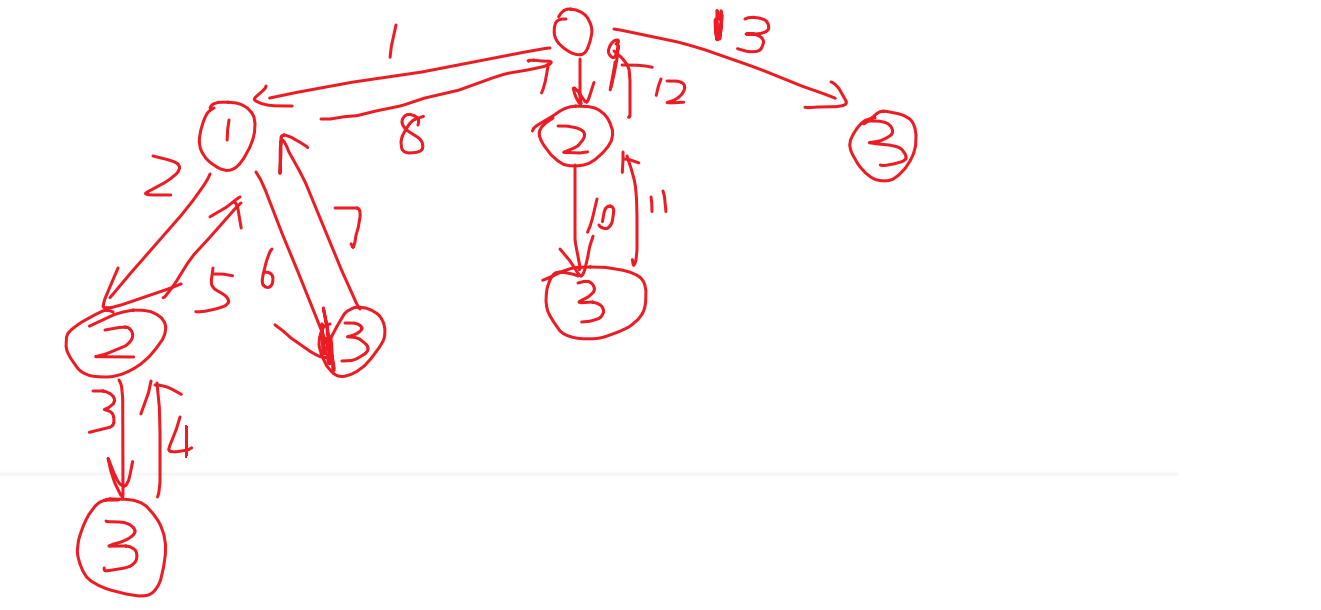
那么根据这个解答树,首先我们的回溯搜索函数应该由这么几部分组成
- 将搜索获得的答案加入到res中。
- for循环遍历搜索下一个元素(比如在初始列表为空的时候,第一位可以选1,2,3显然需要通过循环实现)但是这道题要求的是解集,可以用一个参数currentNum记录下一步循环递归从哪里开始,保证不重复。
- for循环每次dfs后,回溯到原先状态进行下一次dfs。
那么需要哪些参数呢?
基础参数:int nums[],List<Integer> a,List<List<Integer>> ans
此外我们需要一个回溯逻辑,在dfs执行时改变状态,在dfs递归代码执行结束后回到原状态。所以我们需要几个参数来记录完整的原先状态。
回溯参数:boolean[] used,int currentNum
由此代码如下:
public void dfs(int nums[],List<Integer> a,List<List<Integer>> ans,boolean[] used,int currentNum){
//1.将列表加入到ans中
ans.add(new ArrayList<>(a));
//2.递归
for (int i = currentNum; i < nums.length; i++) {
if (used[i]==false){
a.add(nums[i]);
used[i]=true;
dfs(nums,used,i,a,ans);
//3.回溯
used[i]=false;
a.remove(a.size()-1);
}
}
}
class Solution {
public void dfs(int[] nums,boolean[] used,int currentNum,List<Integer> a,List<List<Integer>> ans){
ans.add(new ArrayList<>(a));
//这里非常关键不能add a,因为如果add a的话那么存的就是a的地址,最后ans里全都是a
for (int i = currentNum; i < nums.length; i++) {
if (used[i]==false){
a.add(nums[i]);
used[i]=true;
dfs(nums,used,i,a,ans);
used[i]=false;
a.remove(a.size()-1);
}
}
}
public List<List<Integer>> subsets(int[] nums) {
int len=nums.length;
List<List<Integer>> ans=new ArrayList<>();
List<Integer> a=new ArrayList<>();
boolean[] used=new boolean[len];
for (int i = 0; i < len; i++) {
used[i]=false;
}
dfs(nums,used,0,a,ans);
return ans;
}
}
注意,如果这题不是求子集,而是求由整数数组可以生成的所有列表,那么就不需要记录currentNum,代码如下
class Solution {
public void dfs(int[] nums,boolean[] used,List<Integer> a,List<List<Integer>> ans){
ans.add(new ArrayList<>(a));
//这里非常关键不能add a,因为如果add a的话那么存的就是a的地址,最后ans里全都是a
for (int i = 0; i < nums.length; i++) {
if (used[i]==false){
a.add(nums[i]);
used[i]=true;
dfs(nums,used,a,ans);
used[i]=false;
a.remove(a.size()-1);
}
}
}
public List<List<Integer>> subsets(int[] nums) {
int len=nums.length;
List<List<Integer>> ans=new ArrayList<>();
List<Integer> a=new ArrayList<>();
boolean[] used=new boolean[len];
for (int i = 0; i < len; i++) {
used[i]=false;
}
dfs(nums,used,a,ans);
return ans;
}
}
最终搜索结果如下
