树的遍历顺序及其应用

一、DFS 序

DFS 序就是以 DFS 的方式，记录每一个节点第一次被访问的顺序，这种顺序形成一个形成一个长度为 \(n\) 的序列。主要被用来维护子树信息。有以下特点：

• 对于任意一个点来说，其子树里所有点的 DFS 序是连续的，具体来讲， \(x\) 的子树的所有结点的 DFS 序组成集合恰好构成区间 \([dfn_x,dfn_x+siz_x-1]\)。

• 对于任意一个点来说，存在一条到叶子的路径使得路径上 DFS 序连续。

• 祖先先于后代出现，即若 \(u\) 是 \(v\) 的祖先，则 \(dfn_u<dnf_v\)。

应用一：树链剖分

利用其链连续的特点，一棵树划分为一条条链。

应用二：DFS序优化树上依赖型背包

利用其子树连续的特点，直接做到直接”跳过“子树的贡献。

应用三：子树修改的维护

在DFS序上建立线段树，不多说。

应用四：DFS序求LCA

若 \(u\neq v\)，则它们的 LCA 等于 DFS 序上位置在 \([dfn_u + 1, dfn_v]\) 的深度最小的任意结点的父亲。若 \(u = v\)，则它们的 LCA 就等于 \(u\)。

二、括号序

括号序就是以 DFS 的方式，记录第一节点第一次及最后一次被访问到的顺序，叶子节点也会记录两次，这种顺序形成一个长度为 \(2n\) 的序列。主要被用来维护链信息。有以下特点：

• 一个点被遍历两次视作退出子树，于是可以根据遍历的次数统计链信息，需要特判LCA。

应用一：树上莫队

利用括号序将树上问题转为区间问题从而使用莫队。

三、欧拉序

欧拉徐就是以DFS序的方式，记录每一次被访问到的顺序，一个节点会被算度数次，根节点额外再算一次。这种顺序形成一个长度为 \(2n-1\) 的序列。有以下特点：

• 记录了完整的遍历顺序，可以推导出DFS序与括号序。

• 遍历序列中任何相邻的位置都成父子关系，分为向下与向上两种。

• 任何两点之间的深度最小的节点恰为其 LCA

• 取出根节点的额外一次，任何以一个节点的为根的欧拉序都是以一个特定的节点的欧拉序的循环同构。

应用一：欧拉序求LCA

很简单，就是查两个节点第一次遍历到的编号之间的区间欧拉序最小的节点。

应用二：欧拉序状压DP

方法：设 \(dp_{i,s}\) 表示考虑欧拉序小于等于 \(i\) 的所有节点，其中欧拉序为 \(i\) 的点 \(x\) 到根节点的选择情况为 \(s\) 时的信息。

优势：相邻的两个位置只有向上与向下两种，在于每次是添加叶子节点，往往只需要考虑者单个节点的贡献，而传统的子树 DP 可以看作添加根合并多棵树，往往需要考虑合并子树的复杂度，在合并复杂度高（比如背包）或不能合并的时候考虑。

劣势：由于需要从下还原回上面，所以需要记录到根节点的所有点的状态。导致带一个\(O(2^{dep})\) 的复杂度。常常需要考虑如何减小树高。

应用三：求换根欧拉序

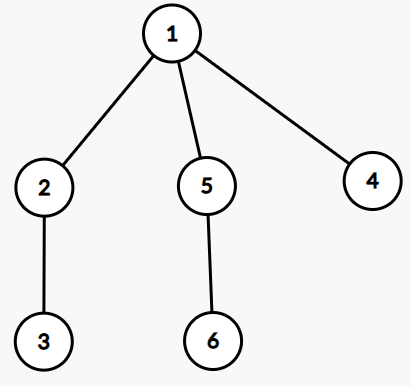
这样子以 \(1\) 为根的欧拉序为：2321565141。

将这串欧拉序延长一倍：123215651412321565141

那么换做是以 \(5\) 为根呢？欧拉序为刚才那个两倍串中标粗的一段：

123215651412321565141、123215651412321565141 这两个都是以 \(5\) 为根的合法括号序

应用四：欧拉序维护直径

例题：Dynamic Diameter

两点之间的距离公式为 \(dis(u,v)=dep_u+dep_v-2dep_{lca(u,v)}\)，加上欧拉序的第三条性质，假设节点 \(x\) 一个遍历的顺序为 \(p_x,a_{p_x}=dep_x\)，则 \(dis_{u,v}=\max_{a_u\le i\le a_v}\{a_{p_x}+a_{p_y}-2a_i\}\)

所以直径 \(D=\max(a_x+a_y-2\min_{i=x}^ya_i)=\max_{x\le i\le y}(a_x+a_y-2a_i)\)。用线段树维护即可。

四、BFS序

BFS序是以BFS的方式，记录每个节点被遍历的顺序，层序遍历是其按深度存储的一种特殊情况。有以下特点：

• 对于任意节点，其儿子遍历相邻。

应用一：维护邻域信息

先将无根树定根，用线段树维护儿子信息，再特判父亲。

例题：Chain Queries