AGC029C Lexicographic constraints
有 \(n\) 个字符串,现在告知它们的长度 \(a_i\),求使得 \(\forall i\in[1,n),s_i<s_{i+1}\) 的最小字符集大小。
\(n\le 2\times 10^5,a_i\le 10^9\)
二分字符集大小 \(|\Sigma|\),分类讨论,设起始字符为 a:
- \(a_i<a_{i+1}\):显然 \(s_{i+1}\leftarrow s_i+(a_{i+1}-a_{i})\times \texttt{a}\) 是最优的;
- \(a_i\ge a_{i+1}\):显然 \(s_{i+1}\) 为 \(s_i\) 长为 \(a_{i+1}\) 的前缀并将最末一位进一是最优的,注意若第一位产生了进位则这个 \(|\Sigma|\) 不合法。
由于 \(a_i\le 10^9\),所以我们并不能开字符串模拟。但是考虑到真正不是 a 的位置只有 \(O(n)\) 数量级,于是我们只要用栈维护这些位置即可。时间复杂度 \(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
struct Node {
int v, c;
Node() {}
Node(int v, int c):v(v), c(c) {}
};
int n;
int top;
int a[200010];
Node sta[200010];
inline void insert(int v, int x) {
while(sta[top].v > v) --top;
if(sta[top].v == v) sta[top].c++;
else sta[++top] = Node(v, 1);
if(top > 1 && sta[top].c == x) --top, insert(v - 1, x);
}
inline int chk(int x) {
sta[top = 1] = Node(0, 0);
for(int i = 2; i <= n; i++)
if(a[i] <= a[i - 1]) insert(a[i], x);
return sta[1].c == 0;
}
int main() {
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
int ct = 0;
for(int i = 2; i <= n; i++) ct += a[i] > a[i - 1];
if(ct == n - 1) return puts("1"), 0;
int l = 2, r = n, res = 1;
while(l <= r) {
int mid = (l + r) >> 1;
if(chk(mid)) res = mid, r = mid - 1;
else l = mid + 1;
} printf("%d\n", res);
return 0;
}
AGC032E Modulo Pairing
给你 \(2n\) 个数,将数两两求和并模 \(m\),求得到的 \(n\) 个数中最大值的最小值。
\(n\le 10^5,a_i<m\le 10^9\)
先对 \(a\) 排序,对于每一对 \((i,j)\),把 \(i,j\) 用一条线连起来。
如果 \(a_i+a_j<M\),则用蓝色线,如果 \(a_i+a_j≥M\),则用红色线。
那么我们可以证明,一定存在一种最优情况,满足:
- 存在一个分界点,使得它左右两侧没有匹配,也就是没有连线经过分界点。
- 只考虑分界点左侧,则最小的数和最大的数连线,第二小的数和第二大的数连线,以此类推。
- 分界点右侧也是一样,最小的和最大的连线。
- 分界点左侧的线的颜色都是蓝色,分界点右侧的线的颜色都是红色。
用图表示就是这样:
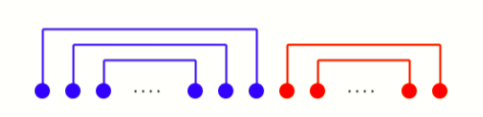
怎么证明它是对的呢?可以使用调整法。
考虑两个数对,如果它们同色但不包含,或者它们异色但不相离,则可以调整成满足条件且不更劣的情况。如图:
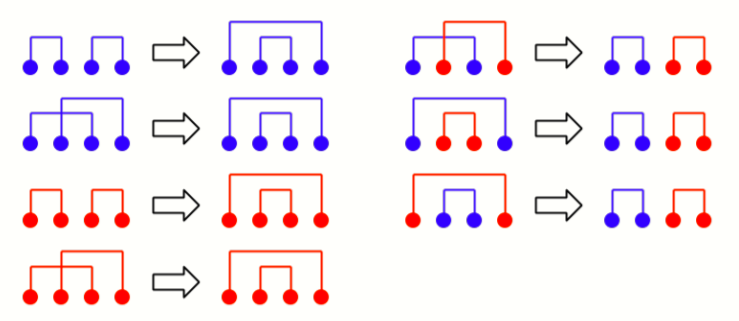
二分分割点即可。时间复杂度 \(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+3;
int n,m,a[maxn];
bool check(int x){
for(int i=x*2+1,j=2*n;i<j;i++,j--)
if(a[i]+a[j]<m) return 0;
return 1;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=2*n;i++) cin>>a[i];
sort(a+1,a+2*n+1);
int l=0,r=n,pos=0;
while(l<=r){
int mid=(l+r)>>1;
if(check(mid)) r=mid-1,pos=mid*2;
else l=mid+1;
}
int ans=0;
for(int i=1,j=pos;i<j;i++,j--)
ans=max(ans,a[i]+a[j]);
for(int i=pos+1,j=2*n;i<j;i++,j--)
ans=max(ans,(a[i]+a[j])-m);
cout<<ans;
return 0;
}
AGC032D Rotation Sort
给你一个排列 \(a\),可以执行以下操作任意次:
- 选定一个区间 \([l,r]\),将 \(a_l\) 放到 \(a_r\) 之后,花费为 \(A\);
- 选定一个区间 \([l,r]\),将 \(a_r\) 放到 \(a_l\) 之前,花费为 \(B\)。
求将排列变为升序的最小花费。
\(n\le 5000\)
显然最多每个数操作一次。分为三类:向前放,不动,向后放。其中不动的元素构成上升子序列。借此可以设计转移,设 \(f(i,j)\) 表示当前在 \(i\),最后一个不动的值为 \(j\),则有转移:
\[f(i,j)=\begin{cases} f(i-1,j)+A&a_i<j\\ \min_{k=1}^{j-1}f(i-1,k)& a_i=j\\ f(i-1,j)+B&a_i>j \end{cases}\]记一个前缀 \(\min\),时间复杂度 \(O(n^2)\),可过。
但是你看这貌似可以上线段树?情况 1,3 相当于区间加。情况 2 相当于区间 \(\min\) + 单点修改,综上时间复杂度 \(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define ls (now<<1)
#define rs (now<<1|1)
using namespace std;
const int maxn=5e3+3;
int n,A,B,a[maxn];
int tag[maxn<<2],mi[maxn<<2];
void pushup(int now){
mi[now]=min(mi[ls],mi[rs]);
}
void pushdown(int now){
if(tag[now]){
mi[ls]+=tag[now];
mi[rs]+=tag[now];
tag[ls]+=tag[now];
tag[rs]+=tag[now];
tag[now]=0;
}
}
void build(int now,int l,int r){
if(l==r){
if(l<a[1]) mi[now]=A;
else if(l==a[1]) mi[now]=0;
else mi[now]=B;
return;
}
int mid=(l+r)>>1;
build(ls,l,mid); build(rs,mid+1,r);
pushup(now);
}
void modify(int now,int l,int r,int L,int R,int x){
if(L<=l&&r<=R){
mi[now]+=x;
tag[now]+=x;
return;
}
pushdown(now);
int mid=(l+r)>>1;
if(L<=mid) modify(ls,l,mid,L,R,x);
if(mid+1<=R) modify(rs,mid+1,r,L,R,x);
pushup(now);
}
void modify(int now,int l,int r,int pos,int x){
if(l==r){
mi[now]=x;
return;
}
pushdown(now);
int mid=(l+r)>>1;
if(pos<=mid) modify(ls,l,mid,pos,x);
else modify(rs,mid+1,r,pos,x);
pushup(now);
}
int query(int now,int l,int r,int L,int R){
if(L<=l&&r<=R){
return mi[now];
}
pushdown(now);
int mid=(l+r)>>1,res=0x3f3f3f3f3f3f3f3f;
if(L<=mid) res=min(res,query(ls,l,mid,L,R));
if(mid+1<=R) res=min(res,query(rs,mid+1,r,L,R));
return res;
}
signed main(){
cin>>n>>A>>B;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
for(int i=2;i<=n;i++){
if(a[i]>1) modify(1,1,n,a[i],query(1,1,n,1,a[i]-1));
if(a[i]>1) modify(1,1,n,1,a[i]-1,A);
if(a[i]<n) modify(1,1,n,a[i]+1,n,B);
}
int ans=0x3f3f3f3f3f3f3f3f;
for(int i=1;i<=n;i++) ans=min(ans,query(1,1,n,i,i));
cout<<ans;
return 0;
}