NOIP将近,由于我实力太菜,所以只能写写真题提升自己了。
P9868 [NOIP2023] 词典
简单字符串题,注意到可以换无限次,所以直接处理出每个字符串中最小的字符数和最大字符数就行了。
#include<bits/stdc++.h>
#define mxn 3010
using namespace std;
char s[mxn][mxn];
int n,m,cnt[mxn][27];
int minn[mxn],maxn[mxn],flg;
int main(){
//freopen("dict.in","r",stdin);
//freopen("a.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>n>>m;
memset(minn,0x3f,sizeof(minn));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
cin>>s[i][j];
cnt[i][s[i][j]-'a'+1]++;
minn[i]=min(minn[i],s[i][j]-'a'+1);
maxn[i]=max(maxn[i],s[i][j]-'a'+1);
}
for(int i=1;i<=n;i++){
flg=1;
for(int j=1;j<=n;j++){
if(i==j)continue;
if(minn[i]<maxn[j])continue;
flg=0;break;
}
if(flg)cout<<1;
else cout<<0;
}
return 0;
}
P9869 [NOIP2023] 三值逻辑
这题折腾了我一下午+三分之一个晚上,我真菜啊。
考虑用并查集将每个操作模拟。
每个值为 \(unknown\) 当且仅当出现两种情况:
\(1.\ x\) 的祖先是 \(-x\)。
\(2.\ x\) 的祖先为 \(unknwon\)。
这样判断就可以了。
同时,发现查询是会有负数,整体右移就行了。
对于死循环的情况,用 \(vis\) 数组判断就行了。
#include<bits/stdc++.h>
#define mxn 100010
#define U 0
#define T 100001
#define F -100001
using namespace std;
int n,m,_,type,ans;
int f[mxn],vis[mxn<<1];
int fnd(int u){
if(u==T||u==F||u==U)return u;
if(vis[-u+n])return U;
if(vis[u+n])return T;
if(u>0){
vis[u+n]=1;
int ret=fnd(f[u]);
f[u]=ret;
vis[u+n]=0;
return ret;
}
else{
vis[u+n]=1;
int ret=fnd(-f[-u]);
vis[u+n]=0;
return ret;
}
return 0;
}
void solve(){
ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++)f[i]=i;
for(int i=1;i<=m;i++){
char opt;cin>>opt;
if(opt=='T'){int x;cin>>x;f[x]=T;}
if(opt=='F'){int x;cin>>x;f[x]=F;}
if(opt=='U'){int x;cin>>x;f[x]=U;}
if(opt=='+'){int x,y;cin>>x>>y;f[x]=f[y];}
if(opt=='-'){int x,y;cin>>x>>y;f[x]=-f[y];}
}
for(int i=1;i<=n;i++)
if(fnd(i)==U)ans++;
cout<<ans<<'\n';
return;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>type>>_;
while(_--)solve();
return 0;
}
P9870 [NOIP2023] 双序列拓展
一开始很容易想到一个 \(35pts\) 的 \(O(qnm)\) 暴力。
根据特殊性质能发现,
我们找到 \(X\) 的最小值与 \(Y\) 的最大值的位置,把那一行和那一列标出来:
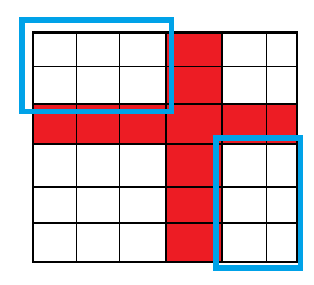
(偷题解的图)
发现如果能从左上角走到红线处,就可以从红线处走到右下角。
于是分治计算就行了。
#include<bits/stdc++.h>
#define ll long long
#define mxn 500010
using namespace std;
struct node{
int minn,maxn;
};
int c,q,a[mxn],b[mxn],xx[mxn],yy[mxn];
node prex[mxn],prey[mxn],sufx[mxn],sufy[mxn];
bool check1(int a,int b,int n,int m){
if(a==1||b==1)return 1;
if(xx[prex[a-1].minn]<yy[prey[b-1].minn])return check1(prex[a-1].minn,b,n,m);
if(xx[prex[a-1].maxn]<yy[prey[b-1].maxn])return check1(a,prey[b-1].maxn,n,m);
return 0;
}
bool check2(int a,int b,int n,int m){
if(a==n||b==m)return 1;
if(xx[sufx[a+1].minn]<yy[sufy[b+1].minn])return check2(sufx[a+1].minn,b,n,m);
if(xx[sufx[a+1].maxn]<yy[sufy[b+1].maxn])return check2(a,sufy[b+1].maxn,n,m);
return 0;
}
bool solve(int x[],int y[],int n,int m){
if(x[1]>=y[1])return 0;
for(int i=1;i<=n;i++)xx[i]=x[i];
for(int i=1;i<=m;i++)yy[i]=y[i];
prex[1]=node{1,1},prey[1]=node{1,1},sufx[n]=node{n,n},sufy[m]=node{m,m};
for(int i=2;i<=n;i++)
prex[i]=node{x[prex[i-1].minn]>x[i]?i:prex[i-1].minn,x[prex[i-1].maxn]<x[i]?i:prex[i-1].maxn};
for(int i=2;i<=m;i++)
prey[i]=node{y[prey[i-1].minn]>y[i]?i:prey[i-1].minn,y[prey[i-1].maxn]<y[i]?i:prey[i-1].maxn};
for(int i=n-1;i;i--)
sufx[i]=node{x[sufx[i+1].minn]>x[i]?i:sufx[i+1].minn,x[sufx[i+1].maxn]<x[i]?i:sufx[i+1].maxn};
for(int i=m-1;i;i--)
sufy[i]=node{y[sufy[i+1].minn]>y[i]?i:sufy[i+1].minn,y[sufy[i+1].maxn]<y[i]?i:sufy[i+1].maxn};
if(x[prex[n].maxn]>=y[prey[m].maxn])return 0;
if(x[prex[n].minn]>=y[prey[m].minn])return 0;
return check1(prex[n].minn,prey[m].maxn,n,m)&&check2(prex[n].minn,prey[m].maxn,n,m);
}
int x[mxn],y[mxn],n,m;
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>c>>n>>m>>q;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=m;i++)cin>>b[i];
if(solve(a,b,n,m)||solve(b,a,m,n))putchar('1');
else putchar('0');
while(q--){
for(int i=1;i<=n;i++)x[i]=a[i];
for(int i=1;i<=m;i++)y[i]=b[i];
int kx,ky;cin>>kx>>ky;
for(int i=1;i<=kx;i++){
int p,v;cin>>p>>v;x[p]=v;
}
for(int i=1;i<=ky;i++){
int p,v;cin>>p>>v;y[p]=v;
}
if(solve(x,y,n,m)||solve(y,x,m,n))putchar('1');
else putchar('0');
}
return 0;
}
P9871 [NOIP2023] 天天爱打卡
有点复杂的dp。
朴素的dp是从左到右遍历,枚举左端点。这样做 \(O(Tnmk)\),会炸飞。
然后我们考虑优化,能不能快速维护区间最大值和区间修改?可以用线段树解决。
#include<bits/stdc++.h>
#define ll long long
#define mxn 100010
#define pll pair<ll,ll>
#define pb push_back
#define mp make_pair
using namespace std;
ll n,m,k,d,c,t;
ll b[mxn<<1],len,cnt,dp[mxn<<1];
struct chlg{
ll x,y,v;
}a[mxn<<1];
vector<pll> p[mxn<<1];
namespace seg{
ll sum[mxn<<3],lazy[mxn<<3];
void push_down(ll rot){
sum[rot<<1]+=lazy[rot],sum[rot<<1|1]+=lazy[rot];
lazy[rot<<1]+=lazy[rot],lazy[rot<<1|1]+=lazy[rot];
lazy[rot]=0;
}
void push_up(ll rot){
sum[rot]=max(sum[rot<<1],sum[rot<<1|1]);
}
void build(ll rot,int l,int r){
sum[rot]=lazy[rot]=0;
if(l==r)return;
int mid=(l+r)>>1;
build(rot<<1,l,mid);
build(rot<<1|1,mid+1,r);
}
void add(ll rot,int l,int r,int x,int y,ll k){
if(l>=x&&r<=y){
sum[rot]+=k,lazy[rot]+=k;
return;
}
push_down(rot);
int mid=(l+r)>>1;
if(x<=mid)add(rot<<1,l,mid,x,y,k);
if(y>mid)add(rot<<1|1,mid+1,r,x,y,k);
push_up(rot);
}
ll query(ll rot,int l,int r,int x,int y){
if(l>=x&&r<=y)return sum[rot];
if(r<x||l>y)return 0;
push_down(rot);
int mid=(l+r)>>1;
return max(query(rot<<1,l,mid,x,y),query(rot<<1|1,mid+1,r,x,y));
}
}
void init(){
cnt=0;
cin>>n>>m>>k>>d;
for(int i=1;i<=m;i++){
cin>>a[i].y>>a[i].x>>a[i].v;
a[i].x=a[i].y-a[i].x+1;
b[++cnt]=a[i].x,b[++cnt]=a[i].y;
}
sort(b+1,b+cnt+1);
len=unique(b+1,b+cnt+1)-b-1;
for(int i=0;i<=len;i++)dp[i]=0;
seg::build(1,1,len);
return;
}
void solve(){
init();
for(int i=1;i<=m;i++){
a[i].x=lower_bound(b+1,b+len+1,a[i].x)-b;
a[i].y=lower_bound(b+1,b+len+1,a[i].y)-b;
p[a[i].y].pb(mp(a[i].x,a[i].v));
}
for(int i=1;i<=len;i++){
for(int j=0;j<p[i].size();j++){
pll pp=p[i][j];
seg::add(1,1,len,1,pp.first,pp.second);
}
dp[i]=max(dp[i],dp[i-1]);
int pos1=lower_bound(b+1,b+len+1,b[i]-k+1)-b;
int pos2=(b[i-1]==b[i]-1)?i-2:i-1;
ll dpi=dp[pos2>=0?pos2:0];
dp[i]=max(dp[i],seg::query(1,1,len,pos1,i-1)-b[i]*d-d);
dp[i]=max(dp[i],seg::query(1,1,len,i,i)+dpi-d);
seg::add(1,1,len,i,i,dpi+b[i]*d);
}
cout<<dp[len]<<'\n';
for(int i=1;i<=len;i++)p[i].clear();
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
cin>>c>>t;
while(t--)solve();
return 0;
}