标签：输出函数得分 ANN 人工神经网络案例神经网络输入神经元

?p=19936

原文出处：拓端数据部落公众号

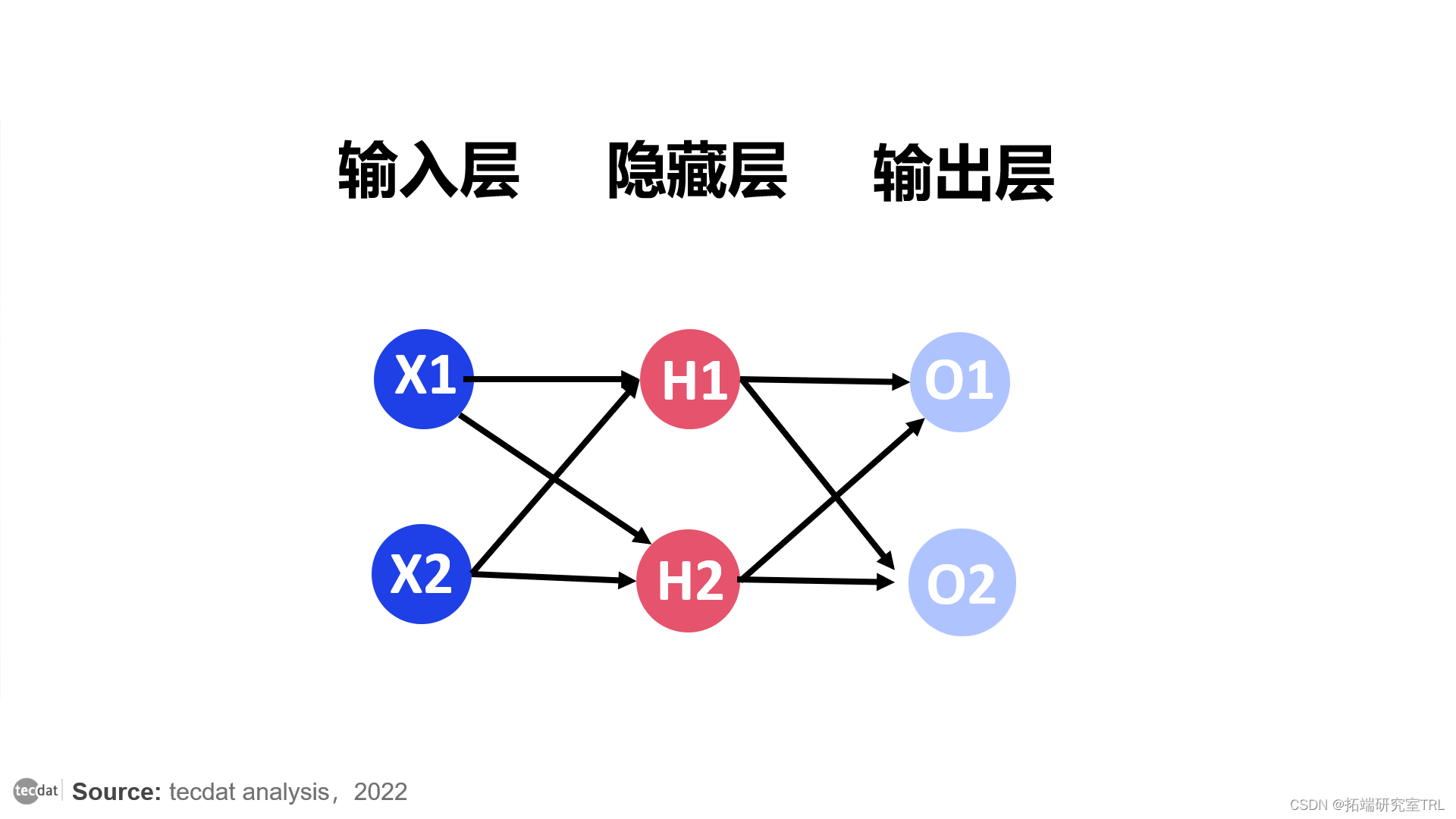
这里考虑人工神经网络具有一个隐藏层，两个输入和输出。

输入为 x1 和 x2。

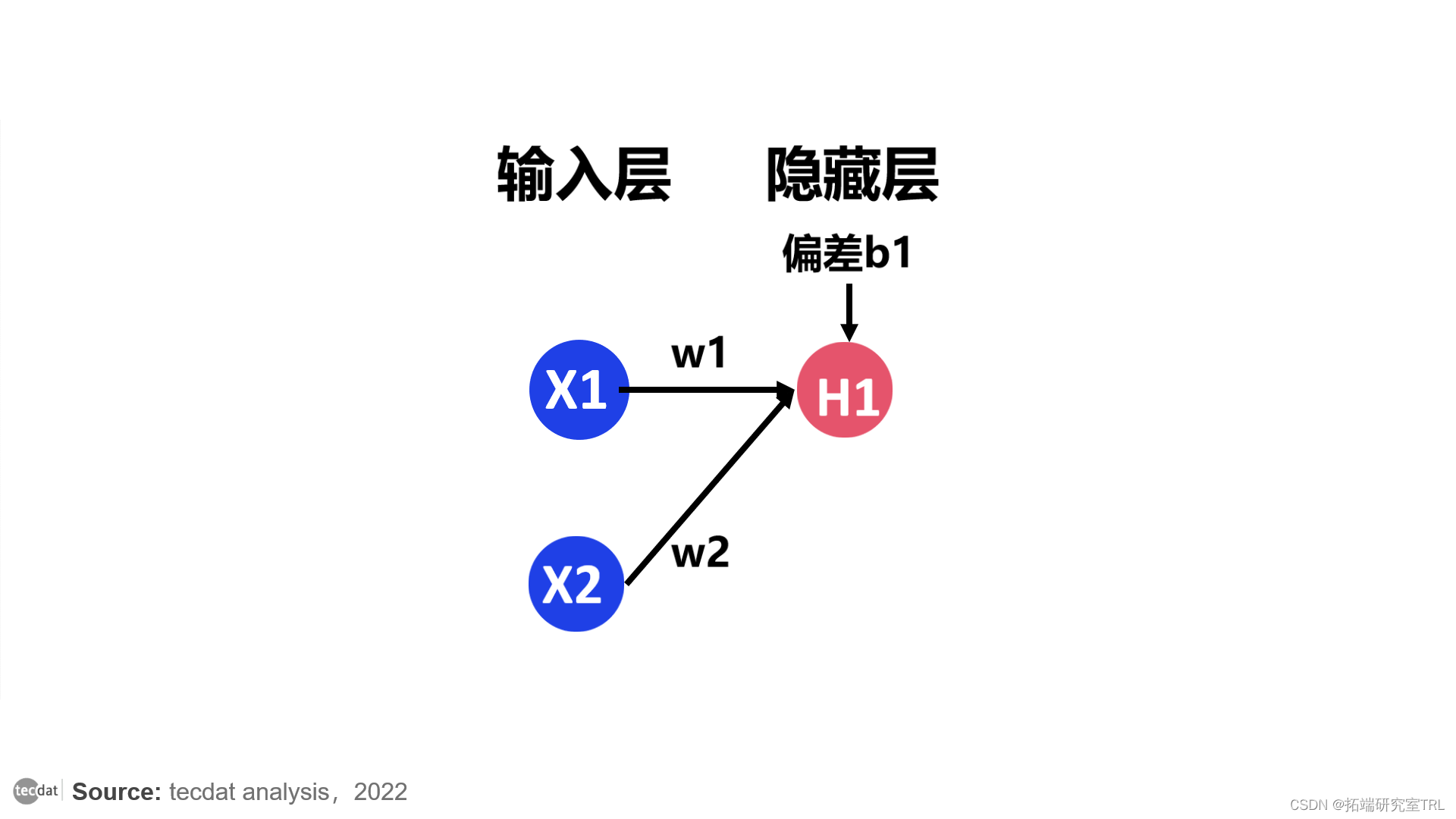
两个权重乘以各自的权重 w1 和 w2。

然后将偏差添加到总和中，并将其称为 z1。

z1 = x1 * w1 + x2 * w2 +b1

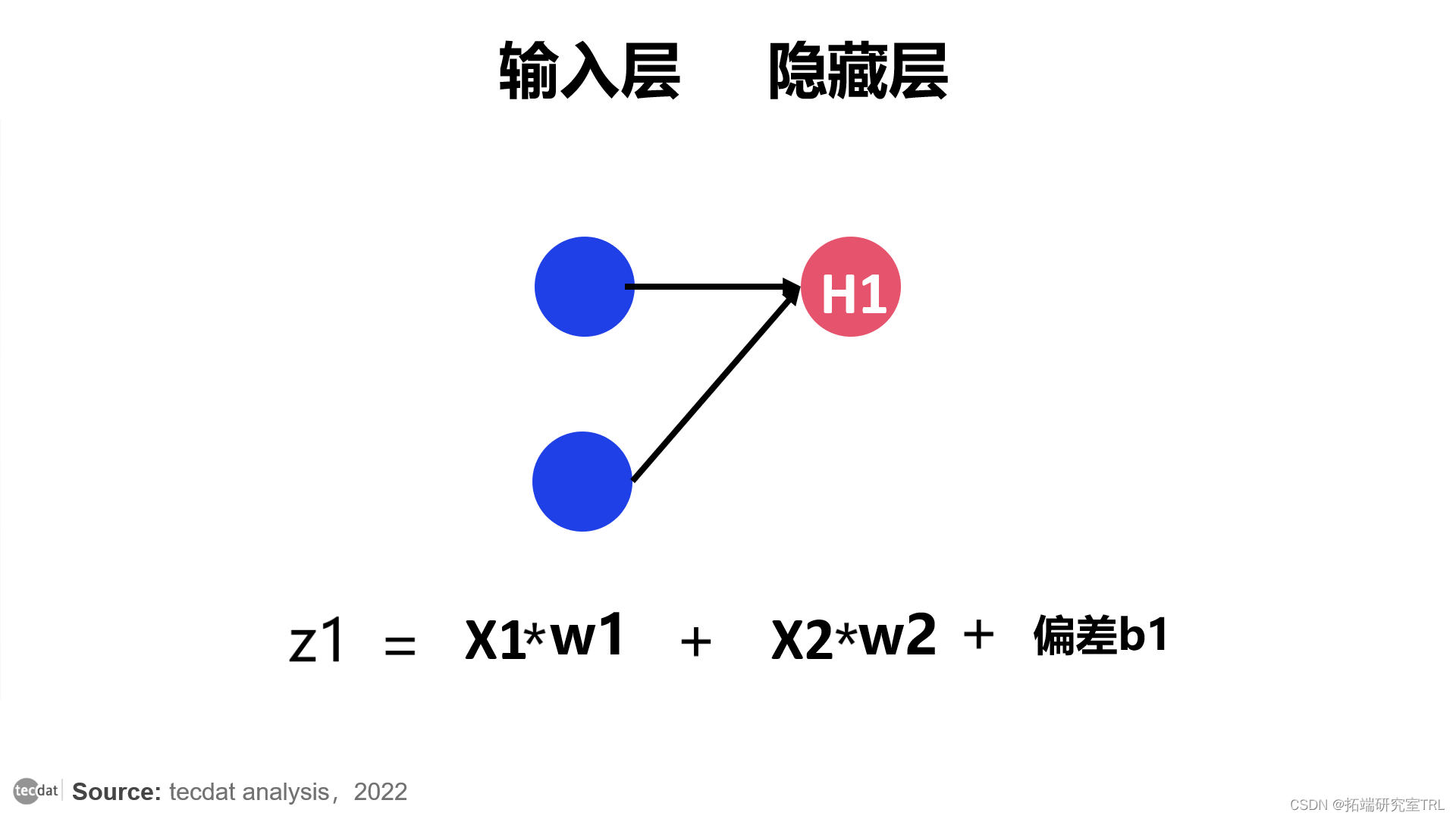
然后应用sigmoid的公式。

隐藏层的输出将成为其右侧下一层的输入。这等于

sigmoid激活函数的公式和图形

隐藏层的第二个节点也以这种方式运行。

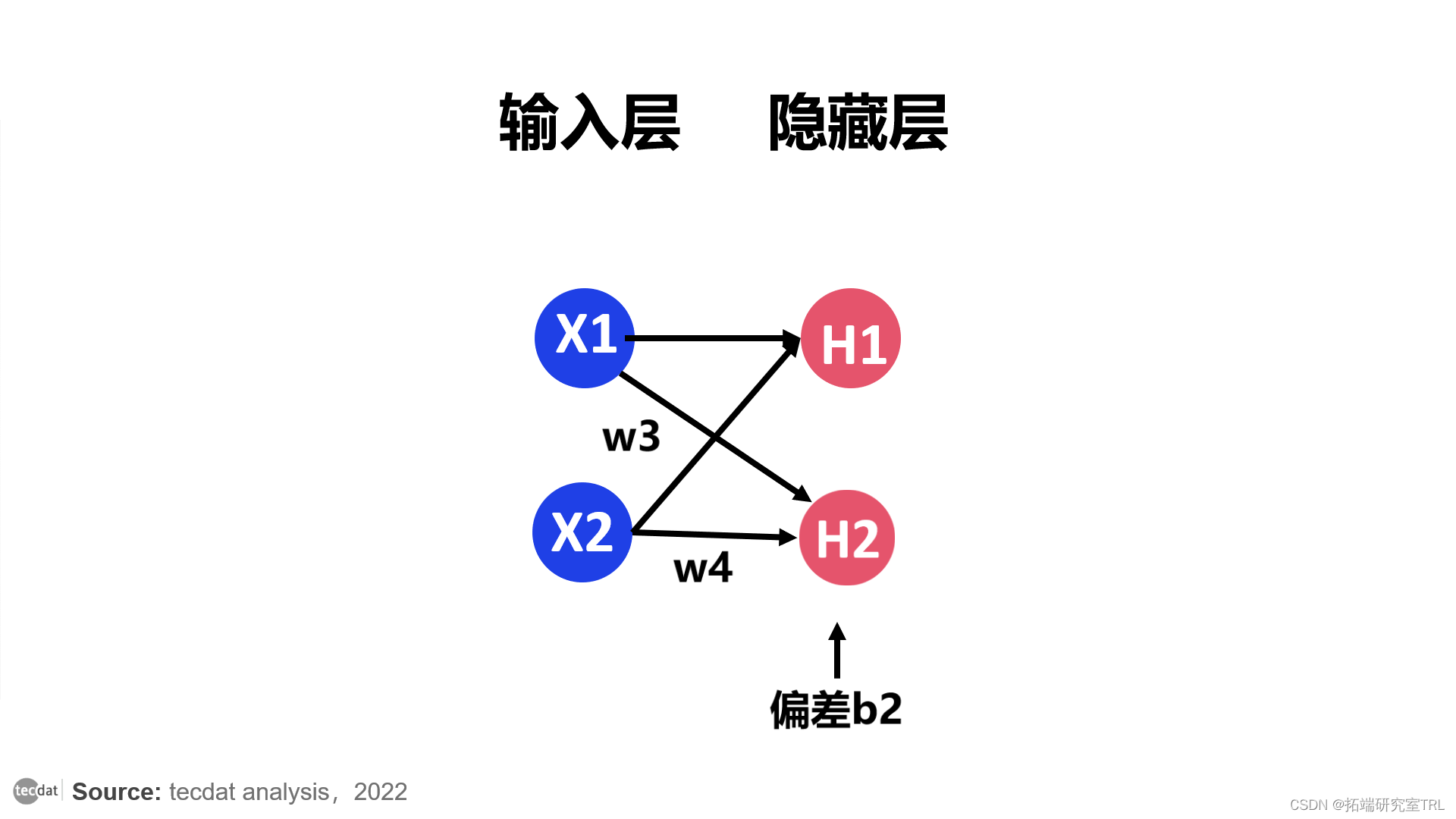
x1 和 x2 输入对于 H1 和 H2 将具有相同的值。但是，H1和H2的权重可能不同，也可能相同。而且，偏差也可以不同，即b1和b2可以不同。

乘以各自的权重w3 和w4。然后将偏差添加到总和中，并将其称为z2。

然后应用sigmoid的公式。此层的输出将是

然后，我们转到下一层。

（输出来自 H1。我们称之为 z1。输出来自 H2，我们称之为 z2。它们进入O1。权重像以前一样乘以相应的输入。

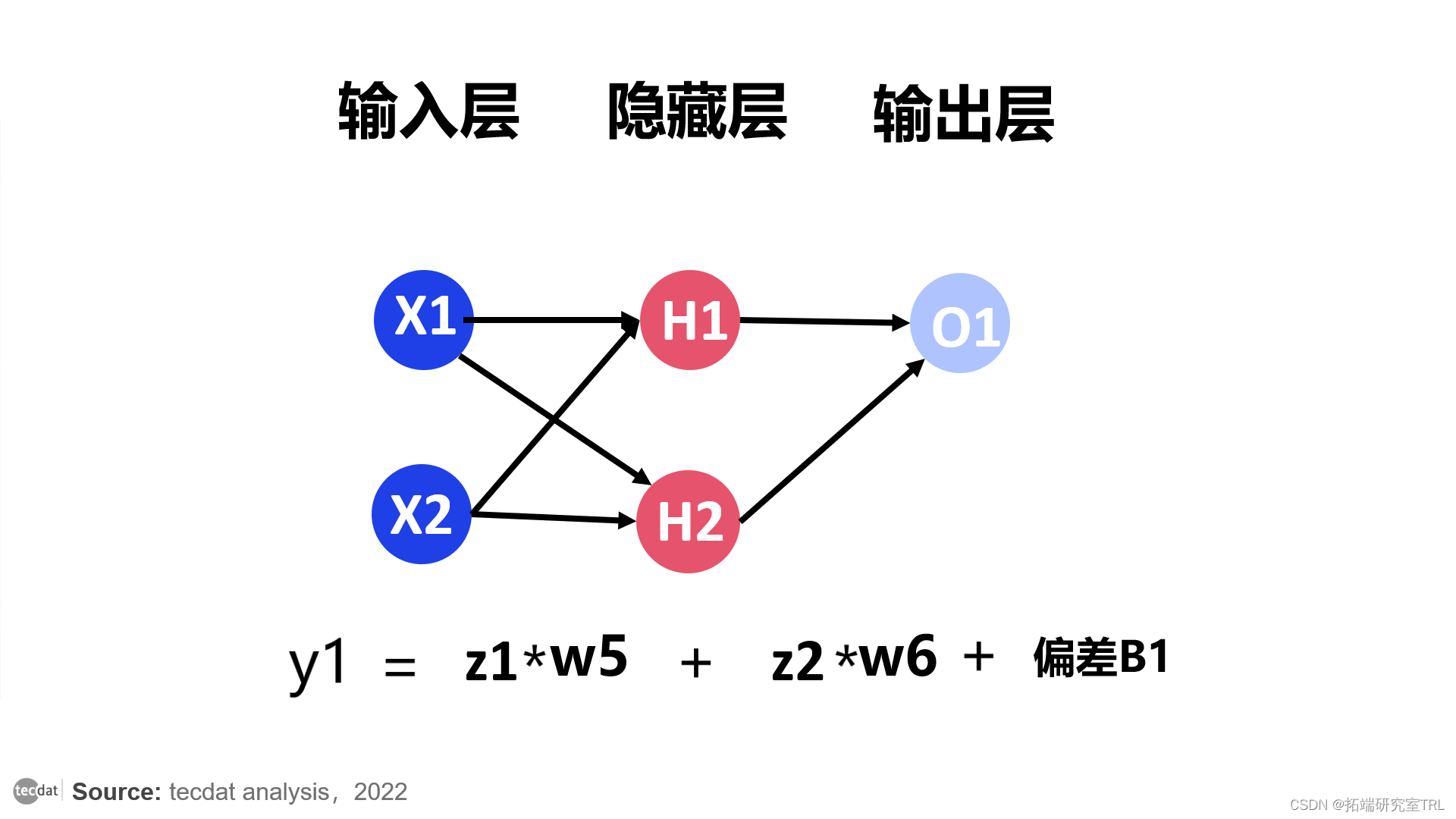
并且，我们选择sigmoid激活函数。因此，O1 的输出为

这里，y1 = z1 * W5 + z2 * W6 + B1

同样，对于O2 的输出，我们再次考虑sigmoid激活函数。

我们将此过程称为前向传播，因为我们总是从左到右。我们从不倒退。

在本教程中，您将学习如何在R中创建神经网络模型。

神经网络（或人工神经网络）具有通过样本进行学习的能力。人工神经网络是一种受生物神经元系统启发的信息处理模型。它由大量高度互连的处理元件（称为神经元）组成，以解决问题。它遵循非线性路径，并在整个节点中并行处理信息。神经网络是一个复杂的自适应系统。自适应意味着它可以通过调整输入权重来更改其内部结构。

该神经网络旨在解决人类容易遇到的问题和机器难以解决的问题，例如识别猫和狗的图片，识别编号的图片。这些问题通常称为模式识别。它的应用范围从光学字符识别到目标检测。

本教程将涵盖以下主题：

神经网络概论
正向传播和反向传播
激活函数
R中神经网络的实现
案例
利弊
结论

神经网络概论

神经网络是受人脑启发执行特定任务的算法。它是一组连接的输入/输出单元，其中每个连接都具有与之关联的权重。在学习阶段，网络通过调整权重进行学习，来预测给定输入的正确类别标签。

人脑由数十亿个处理信息的神经细胞组成。每个神经细胞都认为是一个简单的处理系统。被称为生物神经网络的神经元通过电信号传输信息。这种并行的交互系统使大脑能够思考和处理信息。一个神经元的树突接收来自另一个神经元的输入信号，并根据这些输入将输出响应到某个其他神经元的轴突。

树突接收来自其他神经元的信号。单元体将所有输入信号求和以生成输出。当总和达到阈值时通过轴突输出。突触是神经元相互作用的一个点。它将电化学信号传输到另一个神经元。

x1，x2 .... xn是输入变量。w1，w2 .... wn是各个输入的权重。b是偏差，将其与加权输入相加即可形成输入。偏差和权重都是神经元的可调整参数。使用一些学习规则来调整参数。神经元的输出范围可以从-inf到+ inf。神经元不知道边界。因此，我们需要神经元的输入和输出之间的映射机制。将输入映射到输出的这种机制称为激活函数。

前馈和反馈人工神经网络

人工神经网络主要有两种类型：前馈和反馈人工神经网络。前馈神经网络是非递归网络。该层中的神经元仅与下一层中的神经元相连，并且它们不形成循环。在前馈中，信号仅在一个方向上流向输出层。

反馈神经网络包含循环。通过在网络中引入环路，信号可以双向传播。反馈周期会导致网络行为根据其输入随时间变化。反馈神经网络也称为递归神经网络。

激活函数

激活函数定义神经元的输出。激活函数使神经网络具有非线性和可表达性。有许多激活函数：

识别函数通过激活函数 Identity，节点的输入等于输出。它完美拟合于潜在行为是线性（与线性回归相似）的任务。当存在非线性，单独使用该激活函数是不够的，但它依然可以在最终输出节点上作为激活函数用于回归任务。。
在二元阶梯函数（Binary Step Function）中，如果Y的值高于某个特定值（称为阈值），则输出为True（或已激活），如果小于阈值，则输出为false（或未激活）。这在分类器中非常有用。
S形函数 称为S形函数。逻辑和双曲正切函数是常用的S型函数。有两种：
- Sigmoid函数 是一种逻辑函数，其中输出值为二进制或从0到1变化。
- tanh函数是一种逻辑函数，其输出值在-1到1之间变化。也称为双曲正切函数或tanh。
ReLU函数又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。它是最常用的激活函数。对于x的负值，它输出0。

在R中实现神经网络

创建训练数据集

我们创建数据集。在这里，您需要数据中的两种属性或列：特征和标签。在上面显示的表格中，您可以查看学生的专业知识，沟通技能得分和学生成绩。因此，前两列（专业知识得分和沟通技能得分）是特征，第三列（学生成绩）是二进制标签。

#创建训练数据集
# 在这里，把多个列或特征组合成一组数据
test=data.frame(专业知识,沟通技能得分)


让我们构建神经网络分类器模型。
首先，导入神经网络库，并通过传递标签和特征的参数集，数据集，隐藏层中神经元的数量以及误差计算来创建神经网络分类器模型。

# 拟合神经网络
nn(成绩~专业知识+沟通技能得分, hidden=3,act.fct = "logistic",
linear.output = FALSE)

这里得到模型的因变量、自变量、损失函数、激活函数、权重、结果矩阵（包含达到的阈值，误差，AIC和BIC以及每次重复的权重的矩阵）等信息：

$model.list
$model.list$response
[1] "成绩"
$model.list$variables
[1] "专业知识" "沟通技能得分"
$err.fct
function (x, y)
{
1/2 * (y - x)^2
}
$act.fct
function (x)
{
1/(1 + exp(-x))
}
$net.result
$net.result[[1]]
[,1]
[1,] 0.980052980
[2,] 0.001292503
[3,] 0.032268860
[4,] 0.032437961
[5,] 0.963346989
[6,] 0.977629865
$weights
$weights[[1]]
$weights[[1]][[1]]
[,1] [,2] [,3]
[1,] 3.0583343 3.80801996 -0.9962571
[2,] 1.2436662 -0.05886708 1.7870905
[3,] -0.5240347 -0.03676600 1.8098647
$weights[[1]][[2]]
[,1]
[1,] 4.084756
[2,] -3.807969
[3,] -11.531322
[4,] 3.691784
$generalized.weights
$generalized.weights[[1]]
[,1] [,2]
[1,] 0.15159066 0.09467744
[2,] 0.01719274 0.04320642
[3,] 0.15657354 0.09778953
[4,] -0.46017408 0.34621212
[5,] 0.03868753 0.02416267
[6,] -0.54248384 0.37453006
$startweights
$startweights[[1]]
$startweights[[1]][[1]]
[,1] [,2] [,3]
[1,] 0.1013318 -1.11757311 -0.9962571
[2,] 0.8583704 -0.15529112 1.7870905
[3,] -0.8789741 0.05536849 1.8098647
$startweights[[1]][[2]]
[,1]
[1,] -0.1283200
[2,] -1.0932526
[3,] -1.0077311
[4,] -0.5212917
$result.matrix
[,1]
error 0.002168460
reached.threshold 0.007872764
steps 145.000000000
Intercept.to.1layhid1 3.058334288
专业知识.to.1layhid1 1.243666180
沟通技能得分.to.1layhid1 -0.524034687
Intercept.to.1layhid2 3.808019964
专业知识.to.1layhid2 -0.058867076
沟通技能得分.to.1layhid2 -0.036766001
Intercept.to.1layhid3 -0.996257068
专业知识.to.1layhid3 1.787090472
沟通技能得分.to.1layhid3 1.809864672
Intercept.to.成绩 4.084755522
1layhid1.to.成绩 -3.807969087
1layhid2.to.成绩 -11.531321534
1layhid3.to.成绩 3.691783805

绘制神经网络

让我们绘制您的神经网络模型。

# 绘图神经网络
plot(nn)

创建测试数据集

创建测试数据集：专业知识得分和沟通技能得分

# 创建测试集
test=data.frame(专业知识,沟通技能得分)

预测测试集的结果

使用计算函数预测测试数据的概率得分。

## 使用神经网络进行预测
Pred$result

0.9928202080
0.3335543925
0.9775153014

现在，将概率转换为二进制类。

# 将概率转换为设置阈值0.5的二进制类别
pred <- ifelse(prob>0.5, 1, 0)
pred

预测结果为1,0和1。

利弊

神经网络更灵活，可以用于回归和分类问题。神经网络非常适合具有大量输入（例如图像）的非线性数据集，可以使用任意数量的输入和层，可以并行执行工作。

还有更多可供选择的算法，例如SVM，决策树和回归算法，这些算法简单，快速，易于训练并提供更好的性能。神经网络更多的是黑盒子，需要更多的开发时间和更多的计算能力。与其他机器学习算法相比，神经网络需要更多的数据。NN仅可用于数字输入和非缺失值数据集。一位著名的神经网络研究人员说： “神经网络是解决任何问题的第二好的方法。最好的方法是真正理解问题。”