655. 输出二叉树

655. 输出二叉树

给你一棵二叉树的根节点 root ，请你构造一个下标从 0 开始、大小为 m x n 的字符串矩阵 res ，用以表示树的 格式化布局 。构造此格式化布局矩阵需要遵循以下规则：

• 树的 高度 为 height ，矩阵的行数 m 应该等于 height + 1 。
• 矩阵的列数 n 应该等于 2height+1 - 1 。
• 根节点 需要放置在 顶行 的 正中间 ，对应位置为 res[0][(n-1)/2] 。
• 对于放置在矩阵中的每个节点，设对应位置为 res[r][c] ，将其左子节点放置在 res[r+1][c-2height-r-1] ，右子节点放置在 res[r+1][c+2height-r-1] 。
• 继续这一过程，直到树中的所有节点都妥善放置。
• 任意空单元格都应该包含空字符串 "" 。

返回构造得到的矩阵res 。

示例 1：

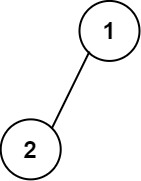
输入：root = [1,2]
输出：
[["","1",""],
 ["2","",""]]

示例 2：

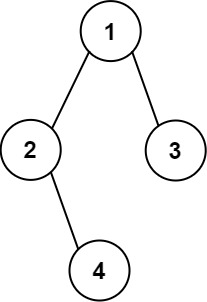
输入：root = [1,2,3,null,4]
输出：
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

提示：

• 树中节点数在范围 [1, 210] 内
• -99 <= Node.val <= 99
• 树的深度在范围 [1, 10] 内

矩阵构造完成，但是插入尝试未果，选择标答（dfs还是不够熟）：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func calDepth(node *TreeNode) int {
    h := 0
    if node.Left != nil {
        h = calDepth(node.Left) + 1
    }
    if node.Right != nil {
        h = max(h, calDepth(node.Right)+1)
    }
    return h
}

func printTree(root *TreeNode) [][]string {
    height := calDepth(root)
    m := height + 1
    n := 1<<m - 1
    ans := make([][]string, m)
    for i := range ans {
        ans[i] = make([]string, n)
    }
    var dfs func(*TreeNode, int, int)
    dfs = func(node *TreeNode, r, c int) {
        ans[r][c] = strconv.Itoa(node.Val)
        if node.Left != nil {
            dfs(node.Left, r+1, c-1<<(height-r-1))
        }
        if node.Right != nil {
            dfs(node.Right, r+1, c+1<<(height-r-1))
        }
    }
    dfs(root, 0, (n-1)/2)
    return ans
}

func max(a, b int)  int {
    if b > a {
        return b
    }
    return a
}