P11208 解题报告

题目传送门

将题意转化一下：将序列变为单调上升等价于逆序对总数量为 \(0\)。

首先看到交换相邻两个数，立马反应过来这种操作最好情况会使逆序对总数减一。

为什么呢？

首先肯定要前面大于后面才交换，否则一定不优。

假设前为 \(i\)，后为 \(j\)，钦定我们计算逆序对的方式是从后往前，依次看每个数后方有多少个小于它的数，并假设 \(i\) 产生的逆序对个数是 \(b_i\)，\(j\) 产生 \(b_j\)，那么交换后，根据逆序对的定义，\(i\) 前方和 \(j\) 后方的逆序对数都不会改变，\(i\) 的逆序对数减一，\(j\) 不变。如下图所示：

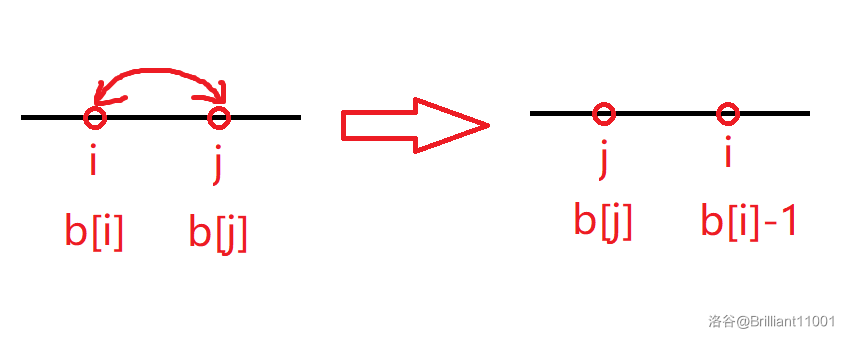
其次发现操作 \(2\) 是个非常硬核的操作：最多操作 \(n - 1\) 次该序列就必定单调递增（毕竟删得只剩一个数了）。

那么可以先设立一个操作次数的上界：\(n - 1\)。

然后，来考虑两种操作结合的情况。

首先不难发现，删除一个数对它后面数的逆序对数不会造成影响，只会将它前面且大于它的数的逆序对数减一，又由于每次只能删除最小的数，所以相当于对所有前面存在的数都要减一。

所以思路就很明了了：建立两个树状数组，一个用来维护逆序对数量，一个用来维护前缀剩下的数的个数，枚举删除那些数然后依次更新答案即可。

（可能只有我傻到去写两个树状数组吧）

\(\texttt{Code:}\)

#include <iostream>

using namespace std;

const int N = 100010;

int n;
int a[N], pos[N];
int invension[N];
//invension[i] 表示第 $i$ 个位置产生多少个逆序对
struct BIT{
    int c[N];
    #define lowbit(x) (x & -x)
    inline void add(int x, int v) {
        for(; x <= n; x += lowbit(x)) c[x] += v;
    }
    inline int ask(int x) {
        int res = 0;
        for(; x; x -= lowbit(x)) res += c[x];
        return res;
    }
}tr1, tr2; //封装数据结构
//tr1 维护逆序对，tr2 维护前缀和

int main() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        pos[a[i]] = i; //记录每个数出现在哪个位置
    }
    long long sum = 0;
    //计算逆序对
    for(int i = n; i; i--) {
        invension[i] = tr1.ask(a[i] - 1);
        sum += invension[i];
        tr1.add(a[i], 1);
    }
    long long ans = min(sum, (long long)n - 1);
    //枚举删除哪些数
    for(int i = 1; i <= n; i++)
        tr2.add(i, 1); //一开始每个位置上都有数
    for(int i = 1; i < n; i++) {
        int cnt = tr2.ask(pos[i] - 1);
        sum -= cnt;
        ans = min(ans, (long long)sum + i);
        tr2.add(pos[i], -1); //删掉后这个位置上就没有数了
    }
    printf("%lld", ans);
    return 0;
}