首页 > 其他分享 >图论基础

图论基础

时间：2024-10-20 09:20:38浏览次数：7  
标签：图论 int top texttt 基础 dfn maxn low

定义与记号

涉及常见或可能用到的概念的定义。关于更多，见参考资料。

基本定义

  • 图：一张图 \(G\) 由若干个点和连接这些点的边构成。称点的集合为 点集 \(V\)，边的集合为 边集 \(E\)，记 \(G = (V, E)\)。
  • 阶：图 \(G\) 的点数 \(|V|\) 称为 阶，记作 \(|G|\)。
  • 无向图：若 \(e \in E\) 没有方向，则称 \(G\) 为 无向图。无向图的边记作 \(e = (u, v)\)，\(u, v\) 之间无序。
  • 有向图：若 \(e \in E\) 有方向，则称 \(G\) 为 有向图。有向图的边记作 \(e = u \to v\) 或 \(e = (u, v)\)，\(u, v\) 之间有序。无向边 \((u, v)\) 可以视为两条有向边 \(u \to v\) 和 \(v \to u\)。
  • 重边：端点和方向（有向图）完全相同的边称为 重边。
  • 自环：连接相同点的边称为 自环。

相邻相关

  • 相邻：在无向图中，称 \(u,v\) 相邻 当且仅当存在 \(e=(u,v)\)。
  • 邻域：在无向图中，点 \(u\) 的 邻域 为所有与之相邻的点的集合，记作 \(N(u)\)。
  • 邻边：在无向图中，与 \(u\) 相连的边 \((u, v)\) 称为 \(u\) 的 邻边。
  • 出边 / 入边：在有向图中，从 \(u\) 出发的边 \(u \to v\) 称为 \(u\) 的 出边，到达 \(u\) 的边 \(v \to u\) 称为 \(u\) 的 入边。
  • 度数：一个点的 度数 为与之关联的边的数量，记作 \(d(u)\)，\(d(u) = \sum_{e \in E} ([u = eu] + [u = ev])\)。每个点的自环对其度数产生 2 的贡献。
  • 出度 / 入度：在有向图中，从 \(u\) 出发的边的数量称为 \(u\) 的 出度，记作 \(d^+(u)\)；到达 \(u\) 的边的数量称为 \(u\) 的 入度，记作 \(d^-(u)\)。
    ta

路径相关

  • 途径：连接一串结点的序列称为 途径，用点序列 \(v_0 \cdots v_k\) 和边序列 \(e_1 \cdots e_k\) 描述，其中 \(e_i = (v_{i-1}, v_i)\)。通常写为 \(v_0 \to v_1 \to \cdots \to v_k\)。
  • 迹：不经过重复边的途径称为 迹。
  • 回路：\(v_0 = v_k\) 的迹称为 回路。
  • 路径：不经过重复点的迹称为 路径，也称 简单路径。不经过重复点比不经过重复边强，所以不经过重复点的途径也是路径。注意题目中的简单路径可能指迹。
  • 环：除 \(v_0 = v_k\) 外所有点互不相同的途径称为 环，也称 圈 或 简单环。

连通性相关

  • 连通：对于无向图的两点 \(u, v\)，若存在途径使得 \(v_0 = u\) 且 \(v_k = v\)，则称 \(u, v\) 连通。
  • 弱连通：对于有向图的两点 \(u, v\)，若将有向边改为无向边后 \(u, v\) 连通，则称 \(u, v\) 弱连通。
  • 连通图：任意两点连通的无向图称为 连通图。
  • 弱连通图：任意两点弱连通的有向图称为 弱连通图。
  • 可达：对于有向图的两点 \(u, v\)，若存在途径使得 \(v_0 = u\) 且 \(v_k = v\)，则称 \(u\) 可达 \(v\)，记作 \(u \Rightarrow v\)。
  • 关于点双连通 / 边双连通 / 强连通，见对应章节。

特殊图

  • 简单图：不含重边和自环的图称为 简单图。
  • 基图：将有向图的所有有向边替换为无向边得到的图称为该有向图的 基图。
  • 有向无环图：不含环的有向图称为 有向无环图，简称 \(\texttt{DAG}\)（\(\texttt{Directed Acyclic Graph}\)）。
  • 完全图：任意不同的两点之间恰有一条边的无向简单图称为 完全图。\(n\) 阶完全图记作 \(K_n\)。
  • 树：不含环的无向连通图称为 树。树是简单图，满足 \(|V|=|E|+1\)。若干棵（包括一棵）树组成的连通块称为 森林。相关知识点见 “树论”。
  • 稀疏图 / 稠密图： \(|E|\) 远小于 \(|V|^2\) 的图称为 稀疏图，\(|E|\) 接近 \(|V|^2\) 的图称为 稠密图。这两个概念没有严格定义，用于讨论时间复杂度为 \(O(|E|)\) 和 \(O(|V|^2)\) 的算法。

子图相关

  • 子图：满足 \(V' \subseteq V\) 且 \(E' \subseteq E\) 的图 \(G' = (V', E')\) 称为 \(G = (V, E)\) 的 子图，记作 \(G' \subseteq G\)。
  • 导出子图：选择若干个点以及两端都在该点集的所有边构成的子图称为该图的 导出子图。导出子图的形态仅由选择的点集 \(V'\) 决定，称点集为 \(V'\) 的导出子图为 \(V'\) 导出的子图，记作 \(G[V']\)。
  • 生成子图：\(|V'| = |V|\) 的子图称为 生成子图。
  • 极大子图（分量）：在子图满足某性质的前提下，称子图 \(G'\) 是 极大 的，当且仅当不存在同样满足该性质的子图 \(G''\) 且 \(G' \subset G'' \subseteq G\)。称 \(G'\) 为满足该性质的 分量，如连通分量，点双连通分量。极大子图不能再扩张。例如，极大的连通的子图称为原图的连通分量，也就是我们熟知的连通块。

约定

  • 一般记 \(n\) 表示点集大小 \(|V|\)，\(m\) 表示边集大小 \(|E|\)。

拓扑排序

计算方法

常用的拓扑排序算法包括基于深度优先搜索（\(\texttt{DFS}\)）的方法和基于入度表（\(\texttt{Kahn}\) 算法）的方法。这里，我将描述基于入度表的方法，这种方法利用队列来实现：

  1. 初始化入度表：遍历图中所有的边，统计每个顶点的入度（即指向该顶点的边的数量）。
  2. 将入度为 \(0\) 的顶点入队：所有在图中入度为 \(0\) 的顶点，都可以作为拓扑排序的起点，将它们加入到一个队列中。
  3. 循环执行以下步骤，直到队列为空：
    • 从队列中取出一个顶点 \(u\)（即当前排序的下一个顶点），并将其输出为结果序列的一部分。
    • 遍历从顶点 \(u\) 出发的所有边 \((u, v)\)，将每个相邻顶点 \(v\) 的入度减 \(1\)（表示边 $ (u, v) $ 被移除）。如果某个顶点 \(v\) 的入度降为 \(0\)，则将 \(v\) 入队。

\(\texttt{DAG}\) 的拓扑序性质很好，常用于解决建图题或图论类型的构造题，常常会将图转化为 \(\texttt{DAG}\)，进行 \(\texttt{dp / dfs}\) 求解。

例 1: B3644 【模板】拓扑排序 / 家谱树

题目描述

有个人的家族很大，辈分关系很混乱，请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列，使得每个人的后辈都比那个人后列出。

第 \(1\) 行一个整数 \(N\)（\(1 \le N \le 100\)），表示家族的人数。接下来 \(N\) 行，第 \(i\) 行描述第 \(i\) 个人的后代编号 \(a_{i,j}\)，表示 \(a_{i,j}\) 是 \(i\) 的后代。每行最后是 \(0\) 表示描述完毕。

输出一个序列，使得每个人的后辈都比那个人后列出。如果有多种不同的序列，输出任意一种即可。

代码

// B3644 【模板】拓扑排序 / 家谱树
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 10000;                                     // 最大顶点数，根据需要修改
int n, x;                                                   // 顶点数
vector<int> Edge[MAXN];                                     // 邻接表表示图
int in_degree[MAXN];                                        // 入度数组
void toposort() {
    queue<int> Q;
    for(int i = 1; i <= n; i++) 
        for(int j : Edge[i]) in_degree[j]++;                // 初始化入度表
    for(int i = 1; i <= n; i++) 
        if(in_degree[i] == 0)  Q.push(i);                   // 将所有入度为0的顶点入队
    while(!Q.empty()) {                                     // 进行拓扑排序
        int u = Q.front(); Q.pop();
        cout << u << " ";                                   // 输出顶点
        for(int i : Edge[u]) {                              // 遍历u的所有邻接点
            in_degree[i]--;
            if(in_degree[i] == 0) 
                Q.push(i);
        }
    }
    cout << endl;
}
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        while (cin >> x && x) 
            Edge[i].push_back(x);
    toposort();
    return 0;
}

例 2: CF463D Gargari and Permutations \(\texttt{*1900}\)

题目描述

给你 \(k\) 个长度为 \(n\) 的排列，求这些排列的最长公共子序列的长度。

思路

先 \(O(kn^2)\) 求出拓扑序。然后按照拓扑序来 \(\texttt{dp}\) 计算。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1010;
int n, m, h[maxn], f[maxn], pos[maxn];
bool flg[maxn][maxn];
vector<int> g[maxn];
int dfs(int u) {
    if (f[u] != -1) return f[u];
    f[u] = 0;
    for (int v : g[u]) f[u] = max(f[u], dfs(v));
    return ++f[u];
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    memset(f, -1, sizeof f);
    memset(flg, 1, sizeof flg);
    cin >> n >> m;
    for (int k = 0; k < m; k++) {
        for (int i = 1, x; i <= n; i++) { cin >> x, pos[x] = i; }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) { flg[i][j] &= pos[i] < pos[j]; }
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (flg[i][j]) g[i].push_back(j);
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) { ans = max(ans, dfs(i)); }
    cout << ans << '\n';
    return 0;
}

最短路问题算法

\(\texttt{Floyd}\) 算法

基本原理

Floyd-Warshall 算法是一种计算图中所有顶点对之间最短路径的算法。

算法流程

  1. 初始化距离矩阵，对角线为0，其他为两点之间的边权重，若无直接边则为无穷大。
  2. 对每个顶点 $k $，更新所有顶点对 $ (i, j) $ 的距离：dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])。
  3. 重复步骤2，直到所有点都被考虑过。

适用场景

适用于计算任意两点间的最短路径，特别是点数量不是很大时效果好。

代码

void floydWarshall() {
    for (int k = 1; k <= n; k++) 
        for (int i = 1; i <=n; i++) 
            for (int j = 1; j <= n; j++) 
                if (dist[i][k] + dist[k][j] < dist[i][j]) 
                    dist[i][j] = dist[i][k] + dist[k][j];
}

\(\texttt{Dijkstra}\) 算法

基本原理

\(\texttt{Dijkstra}\) 算法用于在加权图中找到一个顶点到其他所有顶点的最短路径。

算法流程

  1. 初始化距离数组，源点距离为 \(0\)，其余为无穷大。
  2. 使用优先队列（或堆）来存储所有节点，优先级为节点的当前距离。
  3. 从队列中取出距离最小的节点，更新其相邻节点的距离。
  4. 重复步骤3，直到队列为空或找到目标节点。

适用场景

适用于无负权边的图。

例 1 CF449B Jzzhu and Cities \(\texttt{*2000}\)

题目描述

\(n\) 个点，\(m\) 条带权边的无向图，另外还有 \(k\) 条特殊边，每条边连接 \(1\) 和 \(i\) 。

问最多可以删除这 \(k\) 条边中的多少条，使得每个点到 \(1\) 的最短距离不变。

思路

跑一遍 \(\texttt{Dijkstra}\)，计算出相等路径的条数，判断删除。

代码

// 无向图
#include <bits/stdc++.h>
#define pii pair <int, int>
using namespace std;
const int N = 1e5 + 10;
int n, m, k, x, y, z, ans;
int dist[N], cnt[N], vis[N];
vector < pii > edge[N];
vector < pii > spe;

priority_queue<pii, vector<pii>, greater<pii>> pq;

void dijkstra(int start) {
	for (int i = 1; i <= n; i++) dist[i] = 1e9;
    dist[start] = 0;
    pq.push({0, start});

    while (!pq.empty()) {
        int d = pq.top().first;
        int u = pq.top().second;
        pq.pop();

        if (vis[u]) continue;
		vis[u] = 1;
        for (pii i : edge[u]) {
            if (dist[i.first] == dist[u] + i.second) cnt[i.first]++;
            if (dist[i.first] > dist[u] + i.second) {
                dist[i.first] = dist[u] + i.second;
                cnt[i.first] = 1;
                pq.push({dist[i.first], i.first});
            }
        }
    }
}


int main() {
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++) {
        cin >> x >> y >> z;
        edge[x].push_back({y, z});
        edge[y].push_back({x, z});
    }
    for (int i = 1; i <= k; i++) {
        cin >> y >> z;
        spe.push_back({y, z});
        edge[1].push_back({y, z});
        edge[y].push_back({1, z});
    }
    dijkstra(1); // 算出每一个的距离。
    for (pii i : spe) {
        if (dist[i.first] < i.second) ans++;
        if (dist[i.first] == i.second && cnt[i.first] > 1) 
            ans++, cnt[i.first]--;
    }
    cout << ans << '\n';
}

\(\texttt{SPFA}\) 算法

关于 \(\texttt{SPFA}\), 他 __ 了。

基本原理：
\(\texttt{SPFA}\) 是 \(\texttt{Bellman-Ford}\) 算法的一种改进，用于求解单源最短路径问题。它通过使用队列优化了算法的效率。

算法流程：

  1. 初始化距离数组，源点距离为0，其余为无穷大。
  2. 将源点入队。
  3. 当队列非空时，取出队首元素，遍历其所有出边。
  4. 如果通过当前点可以使得到达某个点的距离更短，则更新距离并将该点入队（如果它当前不在队列中）。
  5. 重复步骤3和4，直到队列为空。

适用场景：
适用于含负权边但无负权回路的图。

\(\texttt{Tarjan}\) 算法

\(\texttt{Trajan}\) 求 \(\texttt{SCC}\)

算法描述

  • \(\texttt{Tarjan}\) 算法用于在有向图中寻找强连通分量（\(\texttt{SCC}\)）。算法通过深度优先搜索（\(\texttt{DFS}\)）遍历图，并利用栈维护访问过的顶点，从而在回溯时能够识别并构成强连通分量。

代码解释

  • s.push(x), vis[x] = 1;：当前顶点 x 入栈，并标记为已访问。
  • dfn[x] = low[x] = ++tim;：为顶点 x 分配一个访问编号和最小可回溯编号。
  • 遍历 x 的每个邻接顶点 i：
    • 如果 i 未被访问（!dfn[i]），递归调用 tarjan(i)，并更新 x 的 low 值。
    • 如果 i 已在栈中（vis[i]），则更新 x 的 low 值。
  • 如果 dfn[x] == low[x]，说明找到了一个强连通分量的根节点：
    • 通过循环将栈中的元素出栈，直到遇到 x，同时为出栈的顶点分配相同的强连通分量编号，并累加对应的值。

复杂度分析

  • 时间复杂度：\(O(V + E)\)，其中 \(V\) 是顶点数，\(E\) 是边数。
  • 空间复杂度：\(O(V)\)，主要是用于存储栈、访问标记、时间戳等信息。

通过这个函数实现，\(\texttt{Tarjan}\) 算法能有效地在有向图中识别所有的强连通分量，并能处理每个分量的累计值问题。希望这样的笔记能帮助您更好地理解和使用 \(\texttt{Tarjan}\) 算法。

代码

void tarjan(int x) {
	s.push(x), vis[x] = 1;
	dfn[x] = low[x] = ++tim;
	for (int i : Edge[x]) {
		if (!dfn[i]) {
			tarjan(i);
			low[x] = min(low[x], low[i]);
			low[x] = min(low[x], dfn[i]);
		} else if (vis[i]) {
			low[x] = min(low[x], dfn[i]);
			low[x] = min(low[x], low[i]);
		}
	}

	if (dfn[x] == low[x]) {
		++count_scc;
		while (s.top() != x) {
			color[s.top()] = count_scc;
			sum[count_scc] += val[s.top()];
			vis[s.top()] = false;
			s.pop();
		}
		color[s.top()] = count_scc;
		sum[count_scc] += val[s.top()];
		vis[s.top()] = false;
		s.pop();
	}
}

例 1: CF949C Data Center Maintenance

题意

题意 : \(n\) 个点，每个点有一个值 \(a_i\)。\(m\) 条边，每个条边链接 \(2\) 个点 \(x，y\) 使得 \(a_x \not =a_y\)。选择最少的 \(k(1 \le k \le n)\) 个点，使 \(a_i = (a_i + 1) \mod h\)，\(m\) 个条件仍成立。

题解

  1. 对于每一条边，如果 \(x_i = y_i + 1\) 则把 \(x_i\) 向 \(y_i\) 连一条边
  2. 缩点
  3. \(\texttt{DAG}\) 上跑没有出度权值最小的点。

代码

#include <bits/stdc++.h>
#define int long long
#define debug(x) cerr << #x << " " << x << '\n';
#define multi false
using namespace std;
const int N = 1e5 + 10;
int t = 1, n, m, h, x, y, tim, scc_count, ansid;
int val[N], dfn[N], low[N], vis[N], color[N], siz[N];
stack <int> s;
vector <int> Edge[N];
vector <int> scc[N];
void tarjan (int x) {
	vis[x] = 1; s.push(x);
	dfn[x] = low[x] = ++tim;
	for (int i : Edge[x]) {
		if (!dfn[i]) {
			tarjan(i);
			low[x] = min(low[x], low[i]);
			low[x] = min(low[x], dfn[i]);
		} else if (vis[i]) {
			low[x] = min(low[x], low[i]);
			low[x] = min(low[x], dfn[i]);
		}
	}
	if (low[x] == dfn[x]) {
		scc_count++;
		while (s.top() != x) {
			color[s.top()] = scc_count;
			vis[s.top()] = 0;
			siz[scc_count]++; 
			s.pop();
		}
		color[s.top()] = scc_count;
		vis[s.top()] = 0;
		siz[scc_count]++; 
		s.pop();
	}
	return;
}
void solve() {
	cin >> n >> m >> h;
	for (int i = 1; i <= n; i++) cin >> val[i];
	for (int i = 1; i <= m; i++) {
		cin >> x >> y;
		if ((val[x] + 1) % h == val[y]) Edge[x].push_back(y);
		if (val[x] == (val[y] + 1) % h) Edge[y].push_back(x);
	}
	for (int i = 1; i <= n; i++) 
		if (!dfn[i]) tarjan(i);
	for (int i = 1; i <= n; i++)
		for (int j : Edge[i])
			if (color[i] != color[j])
				scc[color[i]].push_back(color[j]);
	for (int i = 1; i <= scc_count; i++) 
		if (scc[i].size() == 0 && (siz[i] < siz[ansid] || ansid == 0))
			ansid = i;
	cout << siz[ansid] << '\n';
	for (int i = 1; i <= n; i++)
		if (color[i] == ansid)
			cout << i << ' ';
    return;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    if (multi) cin >> t;
    while (t--) solve();
	return 0;
}

\(\texttt{Trajan}\) 缩点

算法描述

  1. 求出所有的 \(\texttt{SCC}\)。
  2. 对于每个 \(\texttt{SCC}\)，把所有的点缩成一个点。并求出其权值(这个是要根据题意来的，比如例题是求 \(\texttt{SCC}\) 的权值和)。
  3. 对于原图中的每一条边，如果这条边连接的两个点不在同一个 \(\texttt{SCC}\) 中，则把这条边连到两个 \(\texttt{SCC}\) 上。
  4. 对于缩点后的图，形成了一个 \(\texttt{DAG}\)。

例1: P3387

题意

给定一个 \(n\) 个点 \(m\) 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

题解

  1. 求出所有的 \(\texttt{SCC}\)。
  2. 对于每个 \(\texttt{SCC}\)，把所有的点缩成一个点，并求出其权值和。
  3. 对于原图中的每一条边，如果这条边连接的两个点不在同一个 \(\texttt{SCC}\) 中，则把这条边连到两个 \(\texttt{SCC}\) 上。
  4. 对于缩点后的图，形成了一个 \(\texttt{DAG}\)。
  5. 在 \(\texttt{DAG}\) 上跑 \(\texttt{DP}\)，求出路径经过的点权值之和的最大值。

代码

#include <bits/stdc++.h>
#define int long long
#define debug(x) cerr << #x << " " << x << '\n';
#define multi false
using namespace std;
const int N = 1e5 + 10;
const int M = 1e5 + 10;
int t = 1, n, m, tim, count_scc, ans;
int x[M], y[M], val[N], color[N], sum[N], f[N];
int vis[N], low[N], dfn[N];
vector <int> Edge[N];
vector <int> scc[N]; // scc edge
stack <int> s;
void tarjan(int x) {
	s.push(x), vis[x] = 1;
	dfn[x] = low[x] = ++tim;
	for (int i : Edge[x]) {
		if (!dfn[i]) {
			tarjan(i);
			low[x] = min(low[x], low[i]);
			low[x] = min(low[x], dfn[i]);
		} else if (vis[i]) {
			low[x] = min(low[x], dfn[i]);
			low[x] = min(low[x], low[i]);
		}
	}

	if (dfn[x] == low[x]) {
		++count_scc;
		while (s.top() != x) {
			color[s.top()] = count_scc;
			sum[count_scc] += val[s.top()];
			vis[s.top()] = false;
			s.pop();
		}
		color[s.top()] = count_scc;
		sum[count_scc] += val[s.top()];
		vis[s.top()] = false;
		s.pop();
	}
}
int dfs(int x) {
	if (f[x]) return f[x];
	f[x] = sum[x];
	for (int i : scc[x]) 
		f[x] = max(f[x], dfs(i) + sum[x]);
	return f[x];
}
void solve() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> val[i];
	for (int i = 1; i <= m; i++) {
		cin >> x[i] >> y[i];
		Edge[x[i]].push_back(y[i]);
	}
	for (int i = 1; i <= n; i++) 
		if (!dfn[i]) 
			tarjan(i);
	for (int i = 1; i <= m; i++) 
		if (color[x[i]] != color[y[i]])
			scc[color[x[i]]].push_back(color[y[i]]);
	for (int i = 1; i <= n; i++) 
		ans = max(ans, dfs(i));
	cout << ans << '\n';
    return;
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
#endif
    if (multi) cin >> t;
    while (t--) solve();
	return 0;
}

附件

1.png

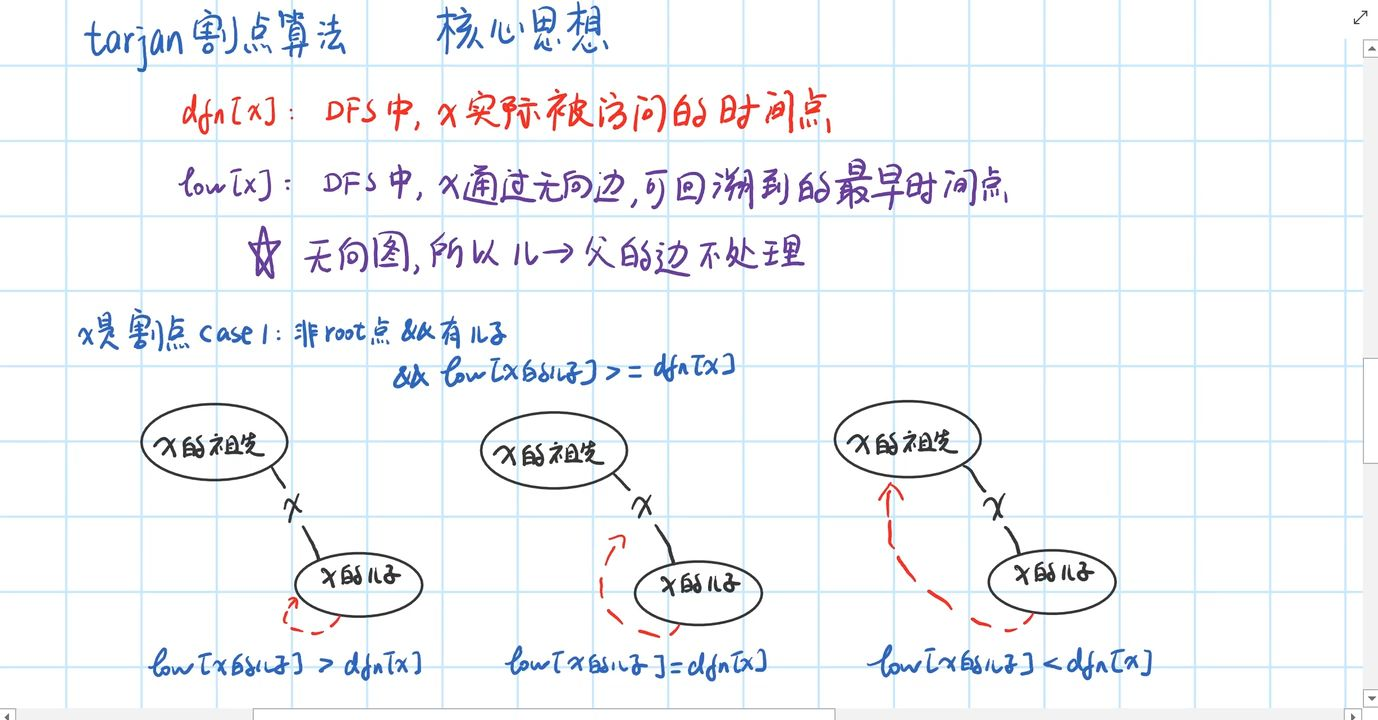
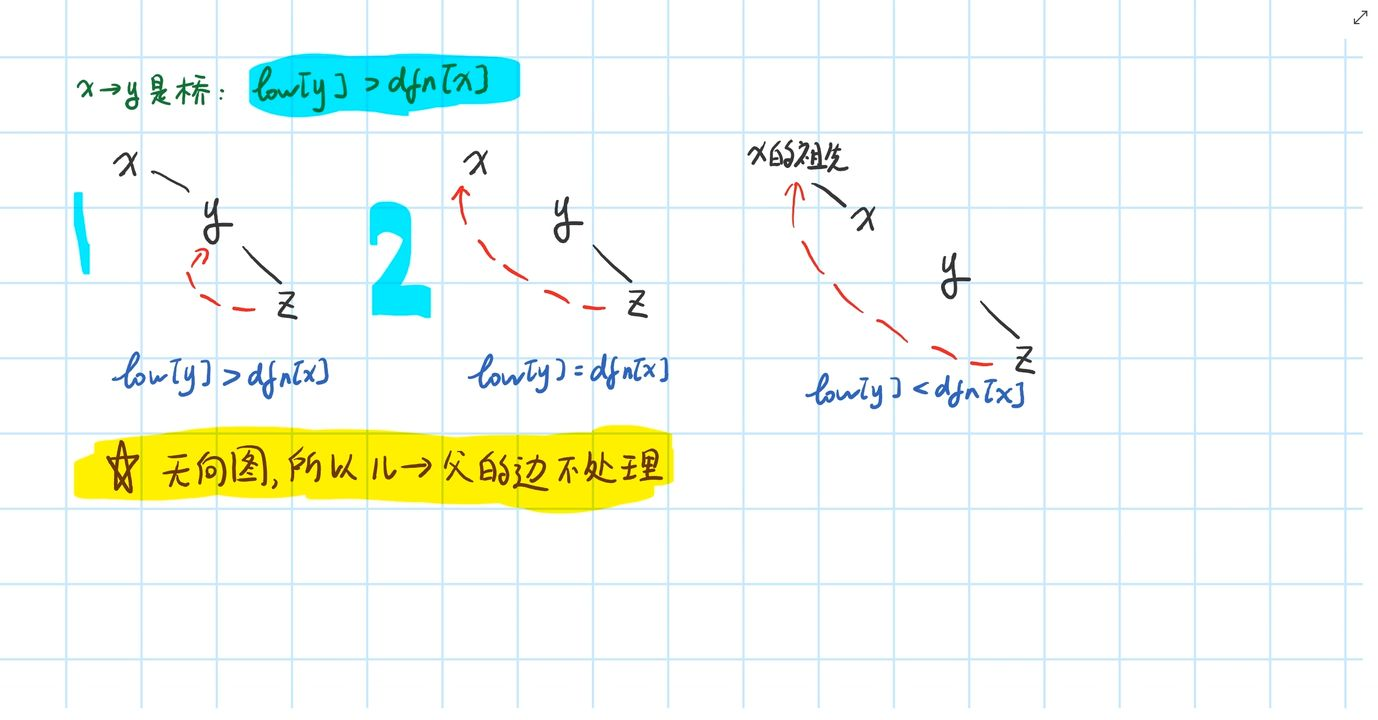
Tarjan 割桥

2.png

\(\texttt{Two-SAT (2-SAT)}\) 问题

算法描述

SAT 是适定性（Satisfiability）问题的简称。一般形式为 k - 适定性问题，简称 k-SAT。而当 \(k>2\) 时该问题为 NP 完全的。所以我们只研究 \(k=2\) 的情况。

2-SAT，简单的说就是给出 \(n\) 个集合，每个集合有两个元素，已知若干个 \(\langle a,b \rangle\)，表示 \(a\) 与 \(b\) 矛盾（其中 \(a\) 与 \(b\) 属于不同的集合）。然后从每个集合选择一个元素，判断能否一共选 \(n\) 个两两不矛盾的元素。显然可能有多种选择方案，一般题中只需要求出一种即可。

常用解决方法

Tarjan SCC 缩点

算法考究在建图这点，我们举个例子来讲：

假设有 \({a1,a2}\) 和 \({b1,b2}\) 两对，已知 \(a1\) 和 \(b2\) 间有矛盾，于是为了方案自洽，由于两者中必须选一个，所以我们就要拉两条有向边 \((a1,b1)\) 和 \((b2,a2)\) 表示选了 \(a1\) 则必须选 \(b1\)，选了 \(b2\) 则必须选 \(a2\) 才能够自洽。

然后通过这样子建边我们跑一遍 Tarjan SCC 判断是否有一个集合中的两个元素在同一个 SCC 中，若有则输出不可能，否则输出方案。构造方案只需要把几个不矛盾的 SCC 拼起来就好了。

输出方案时可以通过变量在图中的拓扑序确定该变量的取值。如果变量 \(x\) 的拓扑序在 \(\neg x\) 之后，那么取 \(x\) 值为真。应用到 Tarjan 算法的缩点，即 \(x\) 所在 SCC 编号在 \(\neg x\) 之前时，取 \(x\) 为真。因为 Tarjan 算法求强连通分量时使用了栈，所以 Tarjan 求得的 SCC 编号相当于反拓扑序。

显然地，时间复杂度为 \(O(n+m)\)。

暴搜

就是沿着图上一条路径，如果一个点被选择了，那么这条路径以后的点都将被选择，那么，出现不可行的情况就是，存在一个集合中两者都被选择了。

那么，我们只需要枚举一下就可以了，数据不大，答案总是可以出来的。


// 来源：刘汝佳白书第 323 页
struct Twosat {
    int n;
    vector<int> g[maxn * 2];
    bool mark[maxn * 2];
    int s[maxn * 2], c;

    bool dfs(int x) {
        if (mark[x ^ 1]) return false;
        if (mark[x]) return true;
        mark[x] = true;
        s[c++] = x;
        for (int i = 0; i < (int)g[x].size(); i++)
            if (!dfs(g[x][i])) return false;
        return true;
    }

    void init(int n) {
        this->n = n;
        for (int i = 0; i < n * 2; i++) g[i].clear();
        memset(mark, 0, sizeof(mark));
    }

    void add_clause(int x, int y) { // 这个函数随题意变化
        g[x].push_back(y ^ 1); // 选了 x 就必须选 y^1
        g[y].push_back(x ^ 1);
    }

    bool solve() {
        for (int i = 0; i < n * 2; i += 2)
            if (!mark[i] && !mark[i + 1]) {
                c = 0;
                if (!dfs(i)) {
                    while (c > 0) mark[s[--c]] = false;
                    if (!dfs(i + 1)) return false;
                }
            }
        return true;
    }
};

例题

例 1 P4782【模板】2-SAT

题目描述

有 \(n\) 个布尔变量 \(x_1\)\(\sim\)\(x_n\)，另有 \(m\) 个需要满足的条件，每个条件的形式都是 「\(x_i\) 为 true / false 或 \(x_j\) 为 true / false」。比如 「\(x_1\) 为真或 \(x_3\) 为假」、「\(x_7\) 为假或 \(x_2\) 为假」。

题目分析

#include <bits/stdc++.h>
using namespace std;
constexpr int N = 2e6 + 5; // 两倍空间
int cnt, hd[N], nxt[N], to[N];
void add(int u, int v) {nxt[++cnt] = hd[u], hd[u] = cnt, to[cnt] = v;}
int n, m, dn, dfn[N], low[N], top, stc[N], vis[N], cn, col[N];
void tarjan(int id) {
  dfn[id] = low[id] = ++dn, vis[id] = 1, stc[++top] = id;
  for(int i = hd[id]; i; i = nxt[i]) {
    int it = to[i];
    if(!dfn[it]) tarjan(it), low[id] = min(low[id], low[it]);
    else if(vis[it]) low[id] = min(low[id], dfn[it]);
  }
  if(low[id] == dfn[id]) {
    col[id] = ++cn;
    while(stc[top] != id) col[stc[top]] = cn, vis[stc[top--]] = 0;
    vis[id] = 0, top--;
  }
}
int main() {
  cin >> n >> m;
  for(int i = 1; i <= m; i++) {
    int u, a, v, b;
    scanf("%d%d%d%d", &u, &a, &v, &b);
    add(u + (!a) * n, v + b * n); // 当 u 等于 !a 时，v 必须等于 b
    add(v + (!b) * n, u + a * n);
  }
  for(int i = 1; i <= n * 2; i++) if(!dfn[i]) tarjan(i); // 遍历所有的点
  for(int i = 1; i <= n; i++) if(col[i] == col[i + n]) puts("IMPOSSIBLE"), exit(0); // 如果两个相互矛盾的在一起（可以互推）-> IMPOSSIBLE
  puts("POSSIBLE");
  for(int i = 1; i <= n; i++) putchar('0' + (col[i + n] < col[i])), putchar(' '); // 选 col 较小的
  return 0;
}

例 2. HDU3062 Party

题目描述

有 n 对夫妻被邀请参加一个聚会，因为场地的问题，每对夫妻中只有 \(1\) 人可以列席。在 \(2n\) 个人中，某些人之间有着很大的矛盾（当然夫妻之间是没有矛盾的），有矛盾的 \(2\) 个人是不会同时出现在聚会上的。有没有可能会有 \(n\) 个人同时列席？

题目分析

按照我们上面的分析，如果 \(a1\) 中的丈夫和 \(a2\) 中的妻子不合，我们就把 \(a1\) 中的丈夫和 \(a2\) 中的丈夫连边，把 \(a2\) 中的妻子和 \(a1\) 中的妻子连边，然后缩点染色判断即可。

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
#define maxn 2018
#define maxm 4000400
using namespace std;
int Index, instack[maxn], DFN[maxn], LOW[maxn];
int tot, color[maxn];
int numedge, head[maxn];

struct Edge {
  int nxt, to;
} edge[maxm];

int sta[maxn], top;
int n, m;

void add(int x, int y) {
  edge[++numedge].to = y;
  edge[numedge].nxt = head[x];
  head[x] = numedge;
}

void tarjan(int x) {  // 缩点看不懂请移步强连通分量上面有一个链接可以点。
  sta[++top] = x;
  instack[x] = 1;
  DFN[x] = LOW[x] = ++Index;
  for (int i = head[x]; i; i = edge[i].nxt) {
    int v = edge[i].to;
    if (!DFN[v]) {
      tarjan(v);
      LOW[x] = min(LOW[x], LOW[v]);
    } else if (instack[v])
      LOW[x] = min(LOW[x], DFN[v]);
  }
  if (DFN[x] == LOW[x]) {
    tot++;
    do {
      color[sta[top]] = tot;  // 染色
      instack[sta[top]] = 0;
    } while (sta[top--] != x);
  }
}

bool solve() {
  for (int i = 0; i < 2 * n; i++)
    if (!DFN[i]) tarjan(i);
  for (int i = 0; i < 2 * n; i += 2)
    if (color[i] == color[i + 1]) return 0;
  return 1;
}

void init() {
  top = 0;
  tot = 0;
  Index = 0;
  numedge = 0;
  memset(sta, 0, sizeof(sta));
  memset(DFN, 0, sizeof(DFN));
  memset(instack, 0, sizeof(instack));
  memset(LOW, 0, sizeof(LOW));
  memset(color, 0, sizeof(color));
  memset(head, 0, sizeof(head));
}

int main() {
  while (~scanf("%d%d", &n, &m)) {
    init();
    for (int i = 1; i <= m; i++) {
      int a1, a2, c1, c2;
      scanf("%d%d%d%d", &a1, &a2, &c1, &c2);  // 自己做的时候别用 cin 会被卡
      add(2 * a1 + c1, 2 * a2 + 1 - c2);
      // 对于第 i 对夫妇，我们用 2i+1 表示丈夫，2i 表示妻子。
      add(2 * a2 + c2, 2 * a1 + 1 - c1);
    }
    if (solve())
      printf("YES\n");
    else
      printf("NO\n");
  }
  return 0;
}

例 3. Gym 101987 TV Show Game

题目描述

有 \(k(k>3)\) 盏灯，每盏灯是红色或者蓝色，但是初始的时候不知道灯的颜色。有 \(n\) 个人，每个人选择 3 盏灯并猜灯的颜色。一个人猜对两盏灯或以上的颜色就可以获得奖品。判断是否存在一个灯的着色方案使得每个人都能领奖，若有则输出一种灯的着色方案。

题目分析

这道题在判断是否有方案的基础上，在有方案时还要输出一个可行解。

根据 伍昱 -《由对称性解 2-sat 问题》，我们可以得出：如果要输出 2-SAT 问题的一个可行解，只需要在 tarjan 缩点后所得的 DAG 上自底向上地进行选择和删除。

具体实现的时候，可以通过构造 DAG 的反图后在反图上进行拓扑排序实现；也可以根据 tarjan 缩点后，所属连通块编号越小，节点越靠近叶子节点这一性质，优先对所属连通块编号小的节点进行选择。

下面给出第二种实现方法的代码。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e4 + 5;
const int maxk = 5005;

int n, k;
int id[maxn][5];
char s[maxn][5][5], ans[maxk];
bool vis[maxn];

struct Edge {
  int v, nxt;
} e[maxn * 100];

int head[maxn], tot = 1;

void addedge(int u, int v) {
  e[tot].v = v;
  e[tot].nxt = head[u];
  head[u] = tot++;
}

int dfn[maxn], low[maxn], color[maxn], stk[maxn], ins[maxn], top, dfs_clock, c;

void tarjan(int x) {  // tarjan算法求强联通
  stk[++top] = x;
  ins[x] = 1;
  dfn[x] = low[x] = ++dfs_clock;
  for (int i = head[x]; i; i = e[i].nxt) {
    int v = e[i].v;
    if (!dfn[v]) {
      tarjan(v);
      low[x] = min(low[x], low[v]);
    } else if (ins[v])
      low[x] = min(low[x], dfn[v]);
  }
  if (dfn[x] == low[x]) {
    c++;
    do {
      color[stk[top]] = c;
      ins[stk[top]] = 0;
    } while (stk[top--] != x);
  }
}

int main() {
  scanf("%d %d", &k, &n);
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= 3; j++) scanf("%d%s", &id[i][j], s[i][j]);

    for (int j = 1; j <= 3; j++) {
      for (int k = 1; k <= 3; k++) {
        if (j == k) continue;
        int u = 2 * id[i][j] - (s[i][j][0] == 'B');
        int v = 2 * id[i][k] - (s[i][k][0] == 'R');
        addedge(u, v);
      }
    }
  }

  for (int i = 1; i <= 2 * k; i++)
    if (!dfn[i]) tarjan(i);

  for (int i = 1; i <= 2 * k; i += 2)
    if (color[i] == color[i + 1]) {
      puts("-1");
      return 0;
    }

  for (int i = 1; i <= 2 * k; i += 2) {
    int f1 = color[i], f2 = color[i + 1];
    if (vis[f1]) {
      ans[(i + 1) >> 1] = 'R';
      continue;
    }
    if (vis[f2]) {
      ans[(i + 1) >> 1] = 'B';
      continue;
    }
    if (f1 < f2) {
      vis[f1] = 1;
      ans[(i + 1) >> 1] = 'R';
    } else {
      vis[f2] = 1;
      ans[(i + 1) >> 1] = 'B';
    }
  }
  ans[k + 1] = 0;
  printf("%s\n", ans + 1);
  return 0;
}

例 4. CF1971H ±1 \(\texttt{*2100}\)

我们发现要想满足要求，就要满足以下条件：

  • 每一列都有且恰好仅有一个 \(-1\)。

我们令 \(g_{i,0}\) 表示 \(a_i\) 必须取 \(-1\)，\(g_{i,1}\) 必须取 \(1\)。

我们考虑两个在同一列的数 \(a_i,a_j\)：

  1. 若 \(a_i<0\wedge a_j<0\)，若 \(-a_i=-1,-a_j=1\)，则 \(a_i=1,a_j=-1\)，将 \(g_{i,1}\) 与 \(g_{j,0}\) 连边。
  2. 若 \(a_i<0\wedge a_j>0\)，若 \(-a_i=-1,a_j=1\)，则 \(a_i=1,a_j=1\)，将 \(g_{i,1}\) 与 \(g_{j,1}\) 连边。
  3. 若 \(a_i>0\wedge a_j<0\)，若 \(-a_i=1,a_j=-1\)，则 \(a_i=-1,a_j=-1\)，将 \(g_{i,0}\) 与 \(g_{j,0}\) 连边。
  4. 若 \(a_i>0\wedge a_j>0\)，若 \(-a_i=1,a_j=1\)，则 \(a_i=-1,a_j=1\)，将 \(g_{i,0}\) 与 \(g_{j,1}\) 连边。

然后跑一遍 \(\texttt{tarjan}\)，求 \(\texttt{SCC}\)，考虑是否有解即可。

Code

网络流

推荐观看：网络流问题基础

给出一个网络图，以及其源点和汇点，求出其网络最大流。

Naive Algorithm

未必能找到最大流，其结果往往比最优解差一点，但是其他更好的算法都基于此算法。

随便找一条路径，然后去 \(\min\)，减去对应的流量，继续，直到不行。

图有点大，点击查看

Ford-Fulkerson Algorithm

关键：构建反向路径时

图有点大，点击查看

图有点大，点击查看

参考资料

施工进度

标签：图论,int,top,texttt,基础,dfn,maxn,low
From： https://www.cnblogs.com/kimi0705/p/-/BasicGraphTheory

相关文章

  • 2024-2025-1 20241328 《计算机基础与程序设计》第四周学习总结
    2024-2025-120241328《计算机基础与程序设计》第四周学习总结作业信息课程2024-2025-1-计算机基础与程序设计作业要求2024-2025-1计算机基础与程序设计第四周作业这个作业的目标门电路，组合电路，逻辑电路，冯诺依曼结构，CPU，内存，IO管理，嵌入式系统，并行结构，物理安全......
  • 【Python】最详细--基础语法
    Python是一种强大且易于学习的编程语言，广泛用于各种应用程序的开发，如web开发、数据科学、人工智能等。以下是一些Python的基础知识：1.Python的注释Python的注释用于在代码中添加说明，以提高代码的可读性。注释在代码执行时会被忽略。单行注释：使用#符号标识，#后面的内容被视为......
  • 2024-2025-1 学号20241315《计算机基础与程序设计》第四周学习总结
    作业信息这个作业属于哪个课程2024-2025-1-计算机基础与程序设计）这个作业要求在哪里https://www.cnblogs.com/rocedu/p/9577842.html#WEEK04这个作业的目标门电路组合电路，逻辑电路冯诺依曼结构CPU，内存，IO管理嵌入式系统，并行结构物理安全作业正文https://www.cn......
  • 2024-2025-1 20241311 《计算机基础与程序设计》第4周学习总结
    2024-2025-120241311《计算机基础与程序设计》第4周学习总结作业信息这个作业属于哪个课程<班级的链接>2024-2025-1-计算机基础与程序设计这个作业要求在哪里<作业要求的链接>2024-2025-1计算机基础与程序设计第一周作业这个作业的目标<写上具体方面>作业正......
  • 网络安全导论（基础讲解）
    编程语言：C语言:一种通用的、面向过程的编程语言，广泛应用于系统软件和嵌入式开发支持面向对象编程，常用于游戏开发、高性能计算等领域C++:在C语言基础上发展而来Java:一种广泛使用的面向对象编程语言，具有跨平台性，应用于企业级应用开发等Python:简洁易学，拥有丰富的库，适用于数......
  • 红队渗透基础——信息收集
    信息收集-web⽹站资产域名后缀注册信息通过⼀些域名注册⽹站来查询⽬标域名的后缀注册情况，看看是否有⼀些其他相关的域名⽹站，如果没有则证明⽬标⽹站可能存在较多的前缀域名⼦⽹站，也为我们进⾏⼦域名的收集，提供了更加精准的收集。微步社区查询通过微步社区的威胁情报......
  • 6-2.Android 对话框之基础对话框问题清单（UI 线程问题、外部取消、冲突问题、dismiss
    对话框对话框（Dialog）是一种常用的UI组件，它主要用于显示信息、接收用户操作反馈对话框可以包含各种元素，但是主要还是以文本、按钮为主，其次是列表其中，基础对话框是Android中最简单的对话框，而后是进度对话框、自定义对话框等一、UI线程问题1、UI线程中创建对话......
  • 图-C++基础
    图论是计算机科学和数学中非常重要的一个分支，涉及到图的性质、结构以及相关的算法。以下是对图论的基础知识、常用算法及其相关代码的整理，帮助你为CSP备考做好准备。一、图的基本概念1.1图的定义在数学中，图是一个由顶点（或节点）和边组成的集合。图可用以下形式表示：无向图：边......
  • 【Java基础】物理内存&虚拟内存
    前言在Java程序运行过程中，操作系统为其分配了物理内存和虚拟内存。理解这两者的概念有助于明晰内存管理和性能优化。一、物理内存物理内存是指计算机的实际RAM（随机存取存储器）。Java进程在运行时需要向操作系统请求内存资源，操作系统通过分配物理内存来满足Java进程的内存......
  • Python基础入门
    目录1.简介2.安装与设置2.1检查是否已安装Python2.2使用Python解释器2.3使用代码编辑器3.Python基础语法3.1注释3.2变量和数据类型3.3输入输出3.4基本运算4.条件语句与循环4.1条件判断4.2循环while循环for循环break与continue5.函数与模块5.1......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99