I - 完美回文

题意

把单词改成一串相同的字母，最小修改次数

思路

把所有字母改成这个单词中出现次数最多的字母

代码

#include <bits/stdc++.h>
using namespace std;

void solve() {
    string s;
    map<char, int> mp;
    cin >> s;
    int mx = 0;
    for (char ch : s) {
        mp[ch]++;
        mx = max(mx, mp[ch]);
    }
    cout << s.size() - mx << '\n';
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) solve();
    return 0;
}

G - 邪恶铭刻

题意

按顺序有三种情况

1获取野兽，攻击力为1
-1合成两只野兽
0选择1或-1

求最后野兽的平均战力最高是多少

思路

贪心的考虑0应该怎么分配

由于算的是平均值，合成野兽的贡献比增加野兽的贡献大，那么尽量选-1，只剩一只野兽的时候再选1

但是如果出现\(1,1,1,0,-1,-1,\) 这种序列，遇到0取-1是无法完成所有事件的

那么可以把0位置记录下来，一旦碰到无法完成所有任务的情况，就把0从-1改成1

代码

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'

void solve() {
    int n;
    cin >> n;
    vector<int> a(n);
    for (int &i : a) cin >> i;
    int cnt = 0;
    int p = 1, q = 1;
    for (int i = 0; i < n; i++) {
        if (a[i] == 1) {
            p++;
            q++;
        } else if (a[i] == -1) {
            if (q > 1) {
                q--;
            } else {
                if (cnt) {
                    p++, q++;
                    cnt--;
                } else {
                    cout << -1 << endl;
                    return;
                }
            }
        } else {
            if (q > 1) {
                q--;
                cnt++;
            } else {
                p++, q++;
            }
        }
    }
    int z = __gcd(p, q);
    cout << p / z << " " << q / z << endl;
}

int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) solve();
    return 0;
}

D - 聊天程序

题意

给初始序列 \(a\)，要求最大化 \(a\) 的第 \(k\) 大的数

可以对 \(a\) 进行如下操作，给定等差数列的长度\(m\)，首项\(c\)，公差\(d\)

选择 \(a\) 的连续序列，把等差数列加上去

最多加1次

思路

采用二分第k大的值

关键在于check函数怎么写

暴力就是枚举每个位置的 \(a_i\) 作为开头，加一遍后看看能不能满足第 \(k\) 大的数大于 \(x\)

即便是暴力方式，也不能每次新建一个数组来排序，我们选择用计数的方式

大于等于 \(x\) 的个数大于等于 \(k\) 说明满足要求（注意这里的第k大是指从大到小排序的第k个数字，不用去重

那么接下来思考优化，对于等差数列，我们先只观察一个位置 以\([1,1,4,5,1,4]\)为例

\(c=1,d=2,m=3\)，那么数列就是\(1,3,5\)

假定二分的第k大的值是4，观察 \(a_4=1\) ，如果 \(a_4\) （下标从0开始）作为等差数列的第二项，是满足要求的

但是如果作为等差数列的第3项，加起来也比4大

那么枚举 \(a_2\) 为开头，从 \(a_2\) 到 \(a_4\) ，排除原本就大于4的值，现在对答案的贡献就是 \(a_4\) 位置的1个

枚举 \(a_3\) 为开头，从 \(a_3\) 到 \(a_5\)，对答案的贡献还是 \(a_4\)

每个位置作为等差开头从而新增的大于 \(x\) 的数量加上原本就大于 \(x\) 的数量如果大于等于 \(k\)，return true

差分维护

代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'

const int N = 2e5 + 10;
int a[N];
int n, k, m, c, d;
int sum[N];
bool check(int x) {
    fill_n(sum, n + 1, 0);
    int cnt = 0;
    for (int i = 0; i < n; i++) {
        if (a[i] < x) {
            int rk;
            if (d != 0) {
                if (x <= a[i] + c)
                    rk = 1;
                else
                    rk = (x - a[i] - c + d - 1) / d + 1;
                if (rk > m) continue;
                if (i - rk + 1 >= 0) sum[i - rk + 1]++;
                if (i - m >= 0) sum[i - m] -= 1;
            } else {
                if (x - a[i] - c <= 0) {
                    rk = 0;
                    sum[i]++;
                    if (i - m >= 0) {
                        sum[i - m] -= 1;
                    }
                }
            }
        } else {
            cnt++;
        }
    }

    for (int i = n - 1; i >= 0; i--) {
        sum[i] += sum[i + 1];
        if (cnt + sum[i] >= k) return 1;
    }

    return 0;
}

void solve() {
    cin >> n >> k >> m >> c >> d;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    int l = 0, r = 1e18;
    int ans = 0;
    while (l <= r) {
        int mid = l + r >> 1;
        if (check(mid)) {
            l = mid + 1;
            ans = mid;
        } else
            r = mid - 1;
    }
    cout << ans;
}

signed main() {
    ios::sync_with_stdio(0), cin.tie(0);
    int t = 1;
    while (t--) {
        solve();
    }
    return 0;
}

A - 停停，昨日请不要再重现

题意

一个棋盘上站满了袋鼠，给操作序列，袋鼠跟随操作序列移动，如果跳出棋盘就移除

棋盘上有个洞，掉进洞的袋鼠也被移除

问最后剩下 \(k\) 只袋鼠的话，有多少可能的位置上有洞，每次棋盘上只有一个洞

思路

在没有洞的情况下，可以判断出最后剩下的袋鼠是一个固定的矩形部分\(n',m'\)

在有洞的情况下，可以看成 \(n'm'\) 固定，这样洞就有一个路径

并且洞的路径不会超，洞的路径与操作相反，L说明洞往右走

而如果洞的路径超了，说明袋鼠全都走出去了，判掉就行

也就是说，我们把洞的路径看成一个方形g，用[[二维差分]]维护一下

\(g[x][y]\) 表示在 \((x,y),(x-U,y-L)\) 这个矩形内的洞经过的格子数

用所有剩下的袋鼠 \(x-g[x][y]\) 就是剩余的袋鼠数

代码

代码抄袭参考这篇

#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
const int N = 1000 + 10;
int n, m, k;
int U, D, L, R, U_, D_, L_, R_;
bool st[N][N]; // stone，表示石头是否存在在这一格
int g[N][N];
string op;

void add(int x1, int y1, int x2, int y2) {
    // 去重，洞走过多次等同于走一次
    if (st[x1][y1]) return;
    st[x1][y1] = true;
    // 差分
    g[x1][y1]++;
    g[x2 + 1][y1]--;
    g[x1][y2 + 1]--;
    g[x2 + 1][y2 + 1]++;
}

void solve() {
    cin >> n >> m >> k >> op;
    // 左上角为坐标原点
    U_ = L_ = U = L = 1;
    R_ = R = m;
    D_ = D = n;
    memset(st, 0, sizeof st);
    memset(g, 0, sizeof g);

    // 确定边界
    for (char ch : op) {
        // 往左，说明左边两行不用了
        if (ch == 'L') L_++, R_++;
        if (ch == 'R') L_--, R_--;
        if (ch == 'U') U_++, D_++;
        if (ch == 'D') U_--, D_--;
        L = max(L, L_);
        R = min(R, R_);
        U = max(U, U_);
        D = min(D, D_);
    }

    // 无袋鼠剩余
    if (U > D || L > R) {
        // 如果k>0 不可能完成，反之，洞随便放
        if (k)
            cout << "0\n";
        else
            cout << n * m << endl;
        return;
    }

    // 统计袋鼠经过格子的情况
    int x = (D - U + 1) * (R - L + 1), cnt = 0;
    add(U, L, D, R);
    for (char ch : op) {
        // 往左，说明洞往右
        if (ch == 'L') L--, R--;
        if (ch == 'R') L++, R++;
        if (ch == 'U') U--, D--;
        if (ch == 'D') U++, D++;
        add(U, L, D, R);
    }

    // 二分前缀和
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            g[i][j] += g[i - 1][j] + g[i][j - 1] - g[i - 1][j - 1];
        }
    }

    // 统计答案
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (x - g[i][j] == k) cnt++;
        }
    }

    cout << cnt << endl;
}

int main() {
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
}

M - 清空水箱

题意

逆时针给一个简单图形，没有交叉和重合，但是有共线的，这个图形是个水箱，里面有水，要开若干个洞才能把水全排出去

疑惑

题解还是挺多的，但是我有个wa30的思路表示十分疑惑，希望有佬能帮我看看哪里有问题

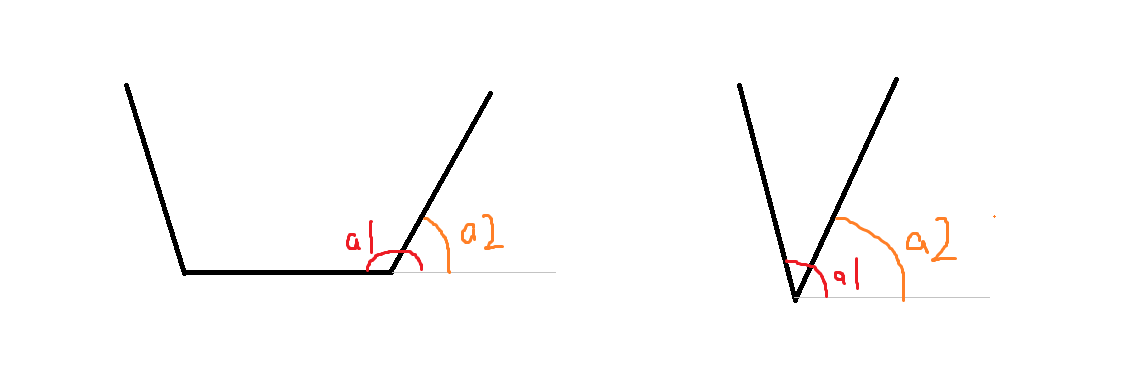
如图，逆时针的话，前一条边的极角是 \(a1\) ，后一条边是 \(a2\)，用 \(atan2\) 函数来算

只要满足 \(a1>0\),\(a2>0\) ,\(a1>a2\)就说明需要开口

代码

#include <bits/stdc++.h>
using namespace std;
#define ld long double
#define endl '\n'
const double eps = 1e-7;
struct P {
    int x, y;
} a[2010];

void solve() {
    int n;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> a[i].x >> a[i].y;
    }
    a[n].x = a[0].x;
    a[n].y = a[0].y;
    a[n + 1].x = a[1].x;
    a[n + 1].y = a[1].y;
    n++;
    int ans = 0;
    for (int i = 1; i < n; i++) {
        long double a1 = atan2l(a[i - 1].y - a[i].y, a[i - 1].x - a[i].x);
        long double a2 = atan2l(a[i + 1].y - a[i].y, a[i + 1].x - a[i].x);
        if (a1 > eps && a2 > eps) {
            if (a2 <= a1) ans++;
        }
    }
    cout << ans << endl;
}
int t = 1;
int main() {
    ios::sync_with_stdio(0), cin.tie(0);
    while (t--) {
        solve();
    }
    return 0;
}