1. 扩散模型（Diffusion Model）的思想

生成图片的过程，很像艺术家雕刻雕像的过程。

艺术家从一块石头开始，逐渐的雕刻出优美的雕像。

同样的，扩散模型从全是噪音的图片开始，逐步降噪，最终生成想要的图片。

• 基本思想
• Q&A
• Denoise的内部结构
• 如何训练 Noise Predicter
• 文生图怎么做

基本思想

扩散模型生成图片分为以下几个步骤：

1. 生成一张只有噪音的图片\(\mathbf{x}_T\)
2. 用一个降噪模型Denoise，对\(\mathbf{x}_T\)进行去噪，得到一张没有那么多噪音的图片\(\mathbf{x}_{T-1}\)
3. 再次使用降噪模型Denoise，对\(\mathbf{x}_{T-1}\)进行去噪，得到一张噪音更少的图片\(\mathbf{x}_{T-2}\)
4. 重复上面的过程\(T\)次，每一次都减少一点图片中的噪音，最终得到我们想要的图片\(\mathbf{x}_0\)

整个过程如下图，这里，我们假设\(T=1000\)

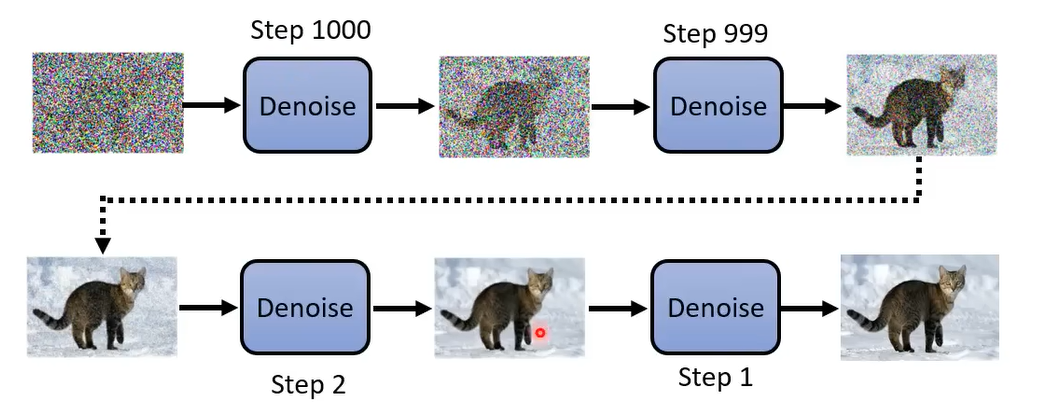
生成图片的过程，很像艺术家雕刻雕像的过程。艺术家从一块石头开始，逐渐的雕刻出优美的雕像。同样的，扩散模型从全是噪音的图片开始，逐渐还原出想要的图片。

Q&A

Q1：在\(T\)步去噪中，每一步的Denoise模型是一样的吗？

A：是一样的。

Q2：Denoise模型以降噪前的图片\(\mathbf{x}_t\)为输入；以降噪后的图片\(\mathbf{x}_{t-1}\)为输出。但是在不同时刻，图片之间的差异是很大的：在开始时刻，图片中的噪音很多；在快要结束的时刻，图片中的噪音很少。在这种情况下，同一个Denoise模型能够很好的完成任务吗？

A：可以给Denoise模型多增加一个输入：除了想要降噪的图片之外，还有当前的时刻\(t\)，以便于Denoise模型对不同的时刻做出不同的反应。如下图，在\(t=1000\)的时刻，Denoise模型接受图片\(\mathbf{x}_{1000}\)和\(1000\)作为输入；在\(t=1\)的时刻，Denoise模型接受图片\(\mathbf{x}_1\)和1作为输入。

Denoise的内部结构

看到这里，可能有的读者会认为，Denoise的输入是：想要降噪的图片\(\mathbf{x}_{t}\)和当前时刻\(t\)；Denoise的输出是：降噪后的图片\(\mathbf{x}_{t-1}\)。

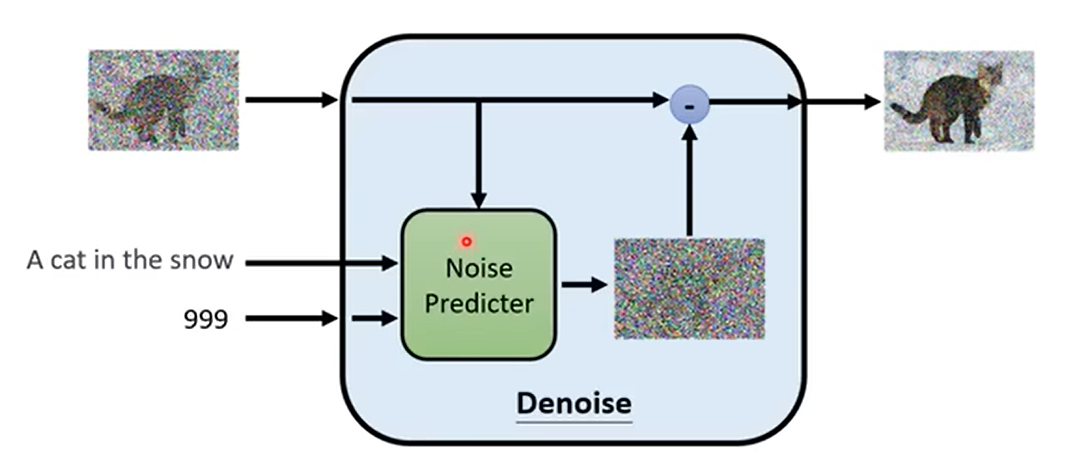
但实际上，Denoise不直接对图片进行预测，而是对当前时刻的噪音\(\boldsymbol{\epsilon_t}\)进行预测。将输入\(\mathbf{x}_{t}\)减去噪音\(\boldsymbol{\epsilon_t}\)，就能得到降噪后的图片\(\mathbf{x}_{t-1}\)。

如下图所示，在Denoise内部，有一个预测噪音的模型Noise Predicter，Noise Predicter接受图片\(\mathbf{x}_t\)和当前时刻\(t\)两个输入，输出当前时刻的噪音\(\boldsymbol{\epsilon_t}\)。最后，将\(\mathbf{x}_t\)减去\(\boldsymbol{\epsilon_t}\)，得到降噪后的图片\(\mathbf{x}_{t-1}\)。

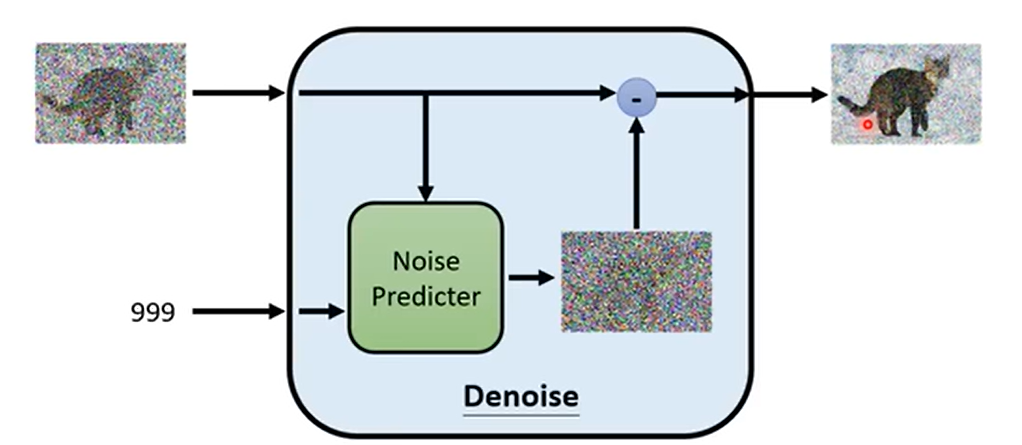
考虑一下，为什么要预测噪音，而不是直接预测图片呢？

因为直接预测图片是很复杂的事情，需要很大的模型才能完成，而预测噪音则简单的多。

如何训练 Noise Predicter

我们可以自己使用一张图片，并人为的向这张图片中逐渐添加噪声，最后形成一张全是噪音的图片，如下图所示

训练 Noise Predicter时，我们的输入（input）是\(t\)时刻的图片\(\mathbf{x}_t\)，以及当前时刻\(t\)；输出是预测的在\(t-1\)时刻向图片中添加的噪音\(\boldsymbol\epsilon_t\)。真实值（ground truth）是实际的在\(t-1\)时刻向图片中添加的噪音。在下图中，输入用蓝色框了起来，真实值用红色框了起来。

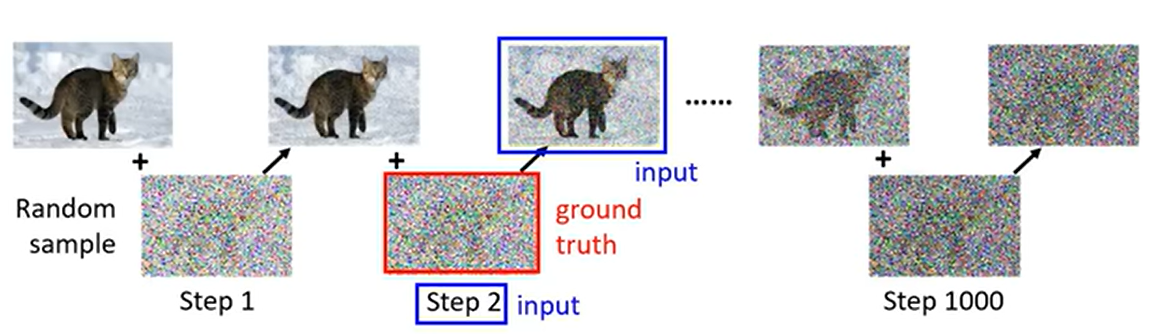
于是，我们就有了Noise Predicter的训练集，其中有两个特征：时刻\(t\)以及当前时刻的图片\(\mathbf{x}_t\)；标签是\(t-1\)时刻向图片中添加的噪音。

根据训练集，就可以训练出一个模型Noise Predicter，通过使用Noise Predicter，我们就可以从满是噪音的图片中逐渐生成想要的图片。

文生图怎么做

如果想要文生图，那么只需要给Denoise增加一个文字输入即可。

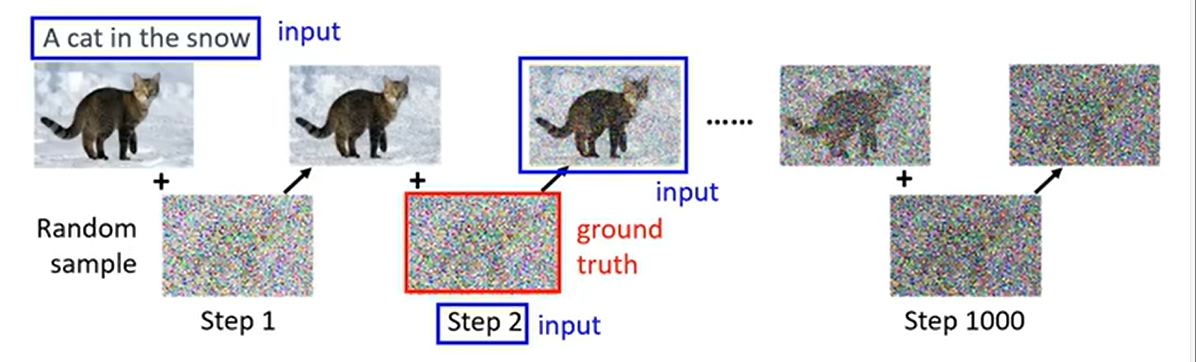
比如说，我给定一段文字：A cat in the snow，想要生成一个图片，那么基本的思想和上面一样。只需要向Denoise添加一个文字输入：A cat in the snow，就可以成功生成一张图片。

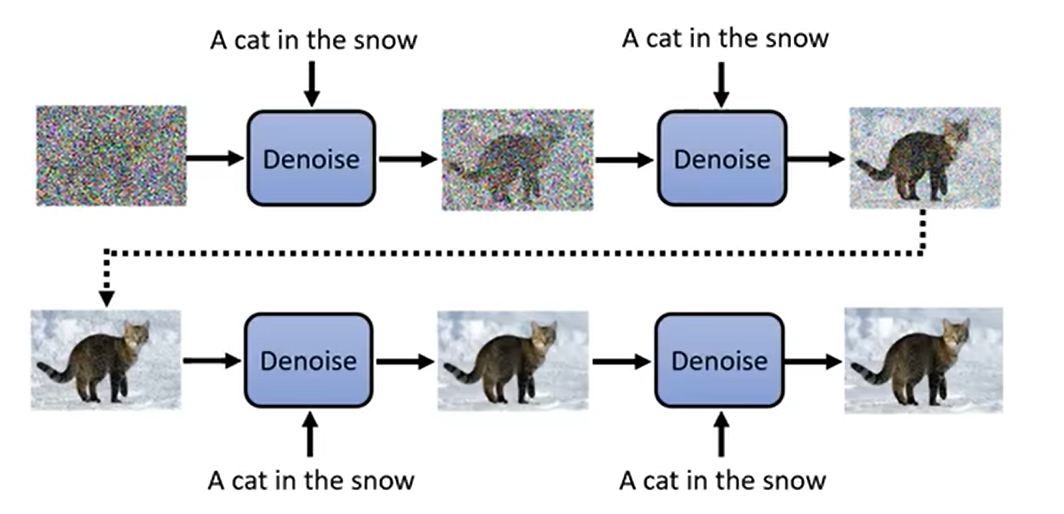
向Denoise添加一个文字输入，实际上就是向Noise Predicter添加一个文字输入。

训练 Noise Predicter的过程也是一样的，只需要加入一个文字输入即可。

在下图中，训练集中有三个特征：时刻\(t\)，当前时刻的图片\(\mathbf{x}_t\)，以及文字A cat in the snow；训练集的标签是是\(t-1\)时刻向图片中添加的噪音。