题目描述
给你一个 \(n\) 个点 \(m\) 条边的图,它是平面上的正 \(n\) 边形和一些对角线,节点按逆时针方向编号为 \(1\) 到 \(n\)。对角线只可能在节点处相交。每条边有一个容量,求每个点对之间的最大流的和。\(n\leq 200000, m\leq 400000\)。
solution
做法
每次找出边权最小的边 \(e\),满足 \(e\) 有恰好一侧是无界的,删去,在它所在的最小环 \(C\) 的其他边的边权加上 \(C\)。最终当图是一棵树时,可以乱做。
证明大概是证了:
-
最小割不经过 \(C\) 的边,或者经过 \(e\) 和 \(C\) 的另外一条边。考虑对偶图,把无界区域划分成 \(n\) 份放到树上,具体不知道。
-
然后通过最小割的性质和构造说明这样改不影响最大流。
平面图对偶图定理
平面图最小割等于对偶图最短路。
实际上这个定理说了和说了一样,含糊不清,我们来点图片:感谢 cjy 老师
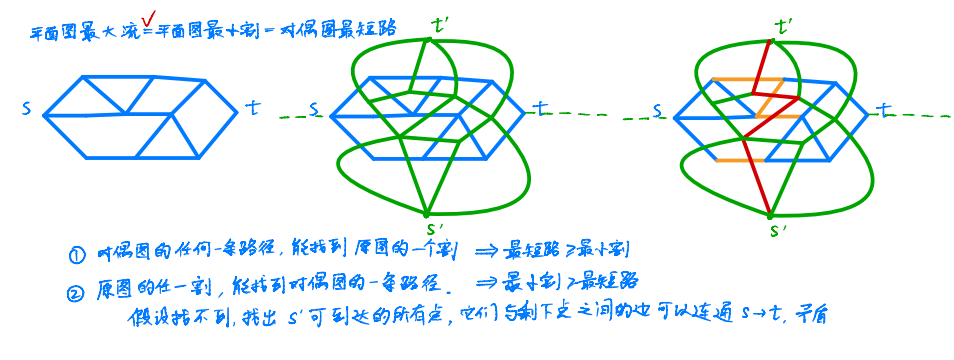
如图,左边那个是平面图。将平面图的每一个面(包括有限面和无限面)当成点,两个面之间的边作为边,建立的图叫作对偶图。然后平面图上 \(s\to t\) 的最小割,是按照 \(\vec{s t}\) 这条直线把无限面切开以后两个无限面的代表点的最短路。可以看看第三幅图,虚线切开了无限面。
交了定义之后要证明原命题。观察到,平面图的每一个割都对应一个对偶图路径,最小割 \(\geq\) 最短路;对偶图的每一条路径都对应了平面图的一个割,可以感性理解一下就是这条路径把平面图劈开了,所以最短路 \(\geq\) 最小割。这么一看最小割 \(=\) 最短路就证完了。
性质一
对于一个包含边 \(e\) 的边数最小环 \(C\),其中 \(e\) 的边权 \(\leq\) (当前连通的)多边形中恰有一侧是无限面(注意表述)的边的边权。那么任意两点(假装是 \(s, t\))的最小割要么不经过 \(C\) 的边,要么经过 \(e\) 和 \(C\) 的另外一条边。
证明。在对偶图上考虑。目测一下因为这个环没有把两个无限面包括进去,所以最短路确实只能是经过了零条或者两条 \(C\) 中的边(不能经过一条边吧,出不去;经过三条边也不优)。考虑为什么它一定能切 \(e\)。
将多边形的每一个顶点向外引一条射线。\(s\) 引出的射线上方和 \(t\) 引出的射线上方交出的无限面是对偶图的起点,可以随意选择一块区域进入;\(s\) 引出的射线下方和 \(t\) 引出的射线下方交出的无限面是对偶图的终点,可以随意选择一块区域离开。
因为我没有数位板所以直接贺课件的图了,不是商用,希望图没事:
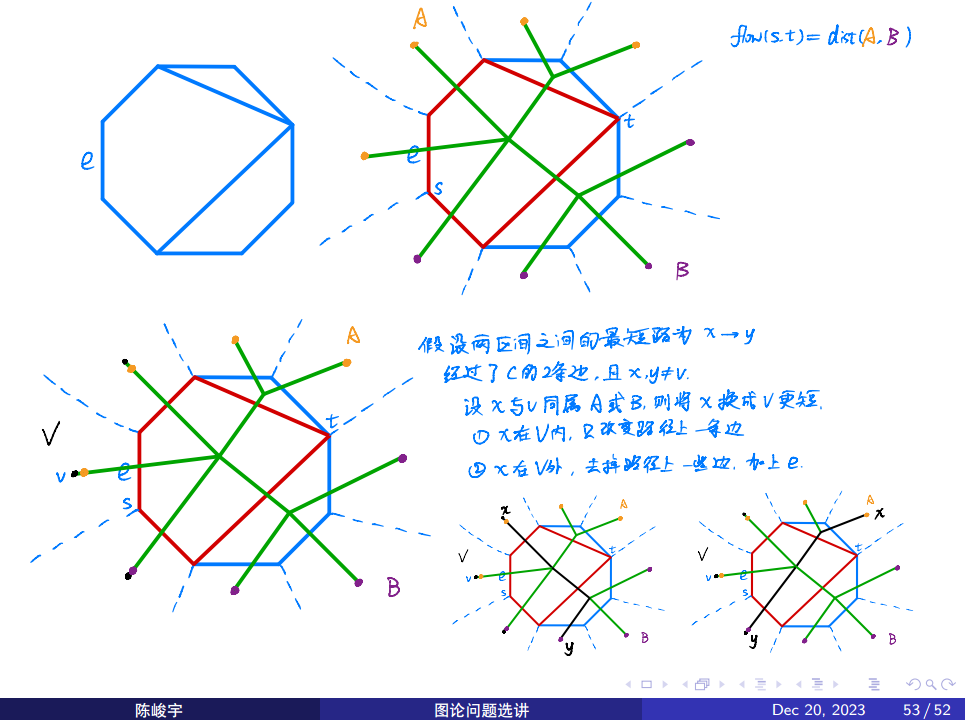
起点是那些黄色点里面选,终点是紫色点里面选,对偶图的边是绿色的,\(C\) 用红色标注。
然后必定经过 \(e\) 就显见了,直接钦定起点跨过 \(e\) 或者终点跨过 \(e\),注意这里的比较对象是蓝边,是说把第一步踩到的蓝边(加上红边)换成 \(e\) 是更优的,即使红边非常短也没有关系。就是右下角的图,原来是 \(x\to y\) 的,你把 \(x\) 搬到 \(v\) 区域内,就能踩到 \(e\) 了。
性质二
删除了多边形上的一条两侧恰好有一侧无界的边 \(e\),并将他的边权加到最小环上,删掉 \(e\),完了以后不影响两个点之间的最大流。
证明。
-
原图最小割 \(\geq\) 新图最小割。
因为如果这个割与 \(C\) 无关,则这个割的大小相同。如果这个割经过 \(e\) 和 \(C\) 的另一条边,则这个割因为改边权大小仍然相同。
-
新图最小割 \(\geq\) 原图最小割。
设新图最小割为 \(E\)。如果 \(E\) 和 \(C\) 无关,则大小相同。否则(注意这个 \(C\) 已经不是环,不能套用性质一),\(E\cup\{e\}\) 是原图的一个割,这个割比 \(E\) 小或者相同。
所以新图最小割 \(=\) 原图最小割。
细节
你发现一旦我们知道树是什么了,可以马上建立 Kruskal 重构树计算答案,因为树上最小割是路径上最小边权,使用这条边作为最小边权的是 Kruskal 重构树上这条边的两个子树跨过去的点对。但是怎么求?
首先就是说找到多边形的最小的“两侧恰有一侧无界”的边 \(e\) 和它所在的最小环 \(C\)。将 \(C\) 上的边边权 \(+e\),然后删去 \(e\)。发现"两侧都无界"的边必然不在其它边的最小环上,也不会被拿出来切掉。所以操作后 \(C\) 中的边会划分"两侧都无界"和“两侧恰有一侧无界”的边,前者加完边权之后就直接被删掉。
如果你真的这样写的话可能会爆炸,不如这样考虑,你建出定理一证明中的对偶图:
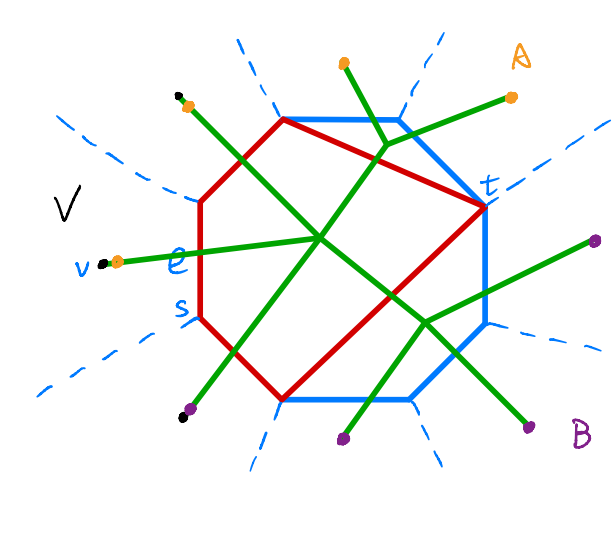
- 先建出这个对偶图(注意对偶图是一棵树),过程等价于划分多边形区域。
随机一个点为一号点,然后随机选方向标号(哦题目标好了是吧),将对角线们的左右两端,强制左 \(<\) 右之后按照左端点降序排序(相同则右端点升序),然后按照顺序拿出一条对角线,将对角线对应的区间的边全部删去并连边后再加入对角线(意思是这个对角线划出了一个新的面,维护一个 map 表示每个位置上的面,每次将那些面拿出来与这次对角线划分出的面连边)。最后 map 还会剩下最后一个跨过 \((1, n)\) 的面也要存下来。 - 维护一个
priority_queue记了边权和边。初始时所有叶子到父亲的边加进去(叶子的父亲明显是它有唯一连边的点)。然后拿一个 \(e\) 出来,它是最小边,在它父亲 \(u\) 那里暴力枚举,除了 \(e\) 之外的边都 \(+e\)。拆掉父亲对应的面之后,这个面就无界了,需要拿父亲的所有边(包括其儿子和父亲)出来枚举,将新的“两侧恰有一侧无界”的边加入优先队列。这里需要维护 \(vis\) 表示每个面是否被拆了(是否无界),初始时所有叶子 \(vis=1\),父亲枚举出边时先将自己 \(vis=1\),然后往 \(vis=0\) 的面插入优先队列(否则一个面会被拆两次)。 - 完了以后 Kruskal 重构树启动就完了。事实上 Kruskal 重构树不需要显式地建出来,而直接写并查集算一下就行。
code
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
using LL = long long;
template <unsigned umod>
struct modint {/*{{{*/
static constexpr int mod = umod;
unsigned v;
modint() = default;
template <class T, enable_if_t<is_integral<T>::value, int> = 0>
modint(const T& y) : v(y % mod + (is_signed<T>() && y < 0 ? mod : 0)) {}
modint& operator+=(const modint& rhs) { v += rhs.v; if (v >= umod) v -= umod; return *this; }
modint& operator-=(const modint& rhs) { v -= rhs.v; if (v >= umod) v += umod; return *this; }
modint& operator*=(const modint& rhs) { v = (unsigned)(1ull * v * rhs.v % umod); return *this; }
modint& operator/=(const modint& rhs) { assert(rhs.v); return *this *= qpow(rhs, mod - 2); }
friend modint operator+(modint lhs, const modint& rhs) { return lhs += rhs; }
friend modint operator-(modint lhs, const modint& rhs) { return lhs -= rhs; }
friend modint operator*(modint lhs, const modint& rhs) { return lhs *= rhs; }
friend modint operator/(modint lhs, const modint& rhs) { return lhs /= rhs; }
template <class T> friend modint qpow(modint a, T b) {
modint r = 1;
for (assert(b >= 0); b; b >>= 1, a *= a) if (b & 1) r *= a;
return r;
}
friend int raw(const modint& self) { return self.v; }
friend ostream& operator<<(ostream& os, const modint& self) { return os << raw(self); }
explicit operator bool() const { return v != 0; }
};/*}}}*/
using mint = modint<998244353>;
template <int N>
struct dsu {
int fa[N + 10], siz[N + 10];
dsu() { for (int i = 1; i <= N; i++) fa[i] = i, siz[i] = 1; }
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
bool merge(int x, int y) {
x = find(x), y = find(y);
if (x == y) return false;
if (siz[x] < siz[y]) swap(x, y);
siz[x] += siz[y], fa[y] = x;
return true;
}
};
template <class T>
using p_queue = priority_queue<T, vector<T>, greater<T>>;
struct range {
int l, r, id;
};
int n, m, fa[400010], upc[400010];
vector<pair<int, LL>> g[400010];
pair<int, int> edg[400010];
LL nw[400010];
bool vis[400010];
dsu<200010> dsy;
void add(int u, int v, LL w) {
if (fa[v] == u) swap(u, v);
if (w == -1e18) nw[u] = -1e18;
else nw[u] += w;
}
int main() {
#ifndef LOCAL
cin.tie(nullptr)->sync_with_stdio(false);
#endif
cin >> n >> m;
vector<range> vec;
map<int, int> mp;
for (int i = 1, u, v, w; i <= m; i++) {
cin >> u >> v >> upc[i];
if (u > v) swap(u, v);
edg[i] = make_pair(u, v);
if (u + 1 == v) mp[u] = i;
else if (u == 1 && v == n) mp[n] = i;
else vec.push_back({.l = u, .r = v, .id = i});
}
sort(vec.begin(), vec.end(), [](range lhs, range rhs) { return lhs.l != rhs.l ? lhs.l > rhs.l : lhs.r < rhs.r; });
for (auto line : vec) {
int p = line.id;
auto it = mp.lower_bound(line.l);
while (it != mp.end() && it->first < line.r) {
fa[it->second] = p;
it = mp.erase(it);
}
mp[line.l] = p;
}
for (auto it : mp) fa[it.second] = m + 1;
for (int i = 1; i <= m; i++) g[fa[i]].emplace_back(i, upc[i]), g[i].emplace_back(fa[i], upc[i]);
p_queue<tuple<LL, int, int>> q;
for (int i = 1; i <= m + 1; i++) if (g[i].size() == 1) q.emplace(g[i][0].second, i, g[i][0].first), vis[i] = true;
while (!q.empty()) {
int u, v;
LL w;
tie(w, u, v) = q.top();
q.pop();
if (vis[v]) add(u, v, w);
else {
vis[v] = true;
add(u, v, -1e18);
for (auto e : g[v]) if (e.first != u) {
if (!vis[e.first]) q.emplace(w + e.second, v, e.first);
else add(v, e.first, w);
}
}
}
vector<tuple<LL, int, int>> t;
for (int i = 1; i <= m; i++) if (nw[i] >= 0) {
t.emplace_back(nw[i], edg[i].first, edg[i].second);
debug("(%d, %d, %lld)\n", edg[i].first, edg[i].second, nw[i]);
}
sort(t.begin(), t.end(), greater<>{});
mint ans = 0;
for (auto&& e : t) {
int u, v;
LL w;
tie(w, u, v) = e;
// ????????????
u = dsy.find(u), v = dsy.find(v);
ans += mint{w} * dsy.siz[u] * dsy.siz[v];
dsy.merge(u, v);
}
cout << ans << endl;
return 0;
}