首页 > 其他分享 >线段树分治略解&杂题解析

线段树分治略解&杂题解析

时间：2024-10-11 21:22:32浏览次数：1  
标签：tmp int 线段 dsu 略解 st num 杂题

可能做到好题之后会再更新吧。

总叙

线段树与离线询问结合技巧又被称为线段树分治。

使用线段树分治维护的信息通常会在某一个时间段内出现，要求在离线的前提下回答某一个时刻的信息并，则可以考虑使用线段树分治的技巧。

以下是线段树分治的基本模板：

change 将信息按时间段覆盖在线段树上，query 通过不断合并线段树上节点维护的信息达到在叶子结点满足信息不重不漏。

struct type_name{};
struct del_tmp{};
struct node{};
struct segment_tree{
	type_name name;
	stack<del_tmp>st;
	struct segment_tree_node{vector<node>v;}t[N<<2];
	inline int ls(int x){return x<<1;};
	inline int rs(int x){return x<<1|1;};
#define mid ((l+r)>>1)
	void change(int p,int l,int r,int re_l,int re_r,node val){
		if(re_l<=l&&r<=re_r)	return t[p].v.push_back(val),void();
		else{
			if(re_l<=mid)	change(ls(p),l,mid,re_l,re_r,val);
			if(mid<re_r)	change(rs(p),mid+1,r,re_l,re_r,val);
		}
	}
	void query(int p,int l,int r){
		int tp=st.tp;
		for(auto it:t[p].v){
			//do sonething to merge information
		}
		if(l==r)	//do something to count answer
		else	query(ls(p),l,mid),query(rs(p),mid+1,r);
		while(st.tp>tp){
			del_tmp tmp=st.top();st.pop();
			//do something to delete
		}
	}
}T;

时间复杂度分析

设总操作数为 $n$，总时间为 $m$，所使用的数据结构满足合并信息的复杂度为 $O(M(n))$，使用栈撤销的时间复杂度为 $O(T(n))$，在叶子结点统计答案的复杂度为 $O(C(n))$。

则每一个操作都在线段树上被分割为 $O(\log{m})$ 段，总共有 $O(n\log{m})$ 段，每一段需要合并一次，删除一次，总复杂度为 $O(n\log{m}(T(n)+M(n)))$。

加上统计答案则为 $O(n\log{m}(T(n)+M(n))+mC(n))$，通常，在题目中，我们限定 $n,m$ 同级。

二分图 /【模板】线段树分治

tips：扩展域并查集判二分图属于线段树分治以外的知识点，请自行了解。

用线段树分治解决问题需要思考以下问题:

  1. 线段树维护什么？

在这里线段树维护的是边，通过边出现的时间将其加入线段树。对应模板中的 node 结构体。

  1. 使用什么数据结构？

这里是按秩合并的并查集，对应模板中的 type_name 结构体。

tips：为什么不能使用路径压缩？

因为路径压缩是均摊复杂度，即 $T(n)$ 可以达到 $O(n)$。会导致撤销的复杂度炸掉。

template<int N>struct DSU{
	int fa[N],siz[N];
	void clear(int n){for(int i=1;i<=n;i++)	fa[i]=i,siz[i]=1;}
	int find(int x){return (fa[x]==x?x:find(fa[x]));}
	del_tmp merge(int x,int y){
		int X=find(x),Y=find(y);
		if(siz[X]>siz[Y])	swap(X,Y);
		del_tmp ret={X,siz[X]};
		siz[Y]+=siz[X],fa[X]=Y;
		return ret;
	}
	bool same(int x,int y){return find(x)==find(y);}
};

3.怎么撤销操作？

通常是使用栈，撤销用模板中的 del_tmp 实现。

while(st.tp>tp){
	del_tmp tmp=st.top();st.pop();
	dsu.siz[dsu.fa[tmp.num]]-=tmp.siz;
	dsu.fa[tmp.num]=tmp.num;
}

4.如何合并信息？

这道题就是使用并查集的 merge 函数完成，在 merge 过程中判断是否合法。

最后在叶子结点根据是否合法输出答案就行了。

code：

struct del_tmp{int num,siz;};
template<int N>struct DSU{
	int fa[N],siz[N];
	void clear(int n){for(int i=1;i<=n;i++)	fa[i]=i,siz[i]=1;}
	int find(int x){return (fa[x]==x?x:find(fa[x]));}
	del_tmp merge(int x,int y){
		int X=find(x),Y=find(y);
		if(siz[X]>siz[Y])	swap(X,Y);
		del_tmp ret={X,siz[X]};
		siz[Y]+=siz[X],fa[X]=Y;
		return ret;
	}
	bool same(int x,int y){return find(x)==find(y);}
};
struct edge{int u,v;};
struct segment_tree{
	DSU<N<<1> dsu;
	my_stack<del_tmp,N<<1>st;
	segment_tree(){dsu.clear((N<<1)-1);}
	struct segment_tree_node{vector<edge>v;}t[N<<2];
	inline int ls(int x){return x<<1;};
	inline int rs(int x){return x<<1|1;};
#define mid ((l+r)>>1)
	void change(int p,int l,int r,int re_l,int re_r,edge val){
		if(re_l<=l&&r<=re_r)	return t[p].v.push_back(val),void();
		else{
			if(re_l<=mid)	change(ls(p),l,mid,re_l,re_r,val);
			if(mid<re_r)	change(rs(p),mid+1,r,re_l,re_r,val);
		}
	}
	void query(int p,int l,int r){
		bool ok=1;int tp=st.tp;
		for(auto it:t[p].v){
			if(dsu.same(it.u,it.v)){
				ok=0;
				for(int i=l;i<=r;i++)	cout<<"No\n";
				break;
			}//小优化，如果在这时已经不合法了，那么到了叶子结点只会增加边，仍然不合法。可以节约递归和删除成本
			st.push(dsu.merge(it.u+N,it.v));
			st.push(dsu.merge(it.v+N,it.u));
		}
		if(ok){
			if(l==r)	cout<<"Yes\n";
			else	query(ls(p),l,mid),query(rs(p),mid+1,r);//一定不能写反
		}
		while(st.tp>tp){
			del_tmp tmp=st.top();st.pop();
			dsu.siz[dsu.fa[tmp.num]]-=tmp.siz;
			dsu.fa[tmp.num]=tmp.num;
		}
	}
}T;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin>>n>>m>>k;
	for(int i=1,u,v,l,r;i<=m;i++){
		cin>>u>>v>>l>>r;
		if(l!=r)	T.change(1,1,k,l+1,r,{u,v});//按时间加边
	}
	T.query(1,1,k);
}

在本题中，$T(n)=O(1)$，$M(n)=O(\log{n})$，$C(n)=O(1)$，所以总的时间复杂度为 $O(m\log{k}(T(n)+M(n))+kC(n))=O(m\log{k}\log{n})$。

tips：本题的第 $i$ 个时间段代表的是开区间 $(i-1,i)$。

Fairy

*2900。

这道题也提示了线段树分治的常见思想：控制边的出现时间。

题目中要求去掉某一条边，这个好办，第 $i$ 条边在第 $i$ 时刻不出现就可以了。

加边：

cin>>n>>m;
for(int i=1,u,v;i<=m;i++){
  cin>>u>>v;
  if(i!=1)	T.change(1,1,m,1,i-1,{u,v});
  if(i!=m)	T.change(1,1,m,i+1,m,{u,v});	
}

其余的部分也就大同小异了。

最小mex生成树

要让 $\operatorname{mex}=k$ 只要没有权值为 $k$ 的边不就行了。

要求去掉某一堆边，这个好办，让权值为 $i$ 的边在第 $i$ 时刻不出现就可以了。

在叶子结点判断剩余的边是否能构成原图的生成树即可。

query：

void query(int p,int l,int r){
  int tp=st.tp;
  for(auto it:t[p].v)	st.push(dsu.merge(it.u,it.v));
  if(dsu.siz[dsu.find(1)]==n)	ans=min(ans,l);
  else if(l!=r)	query(ls(p),l,mid),query(rs(p),mid+1,r);
  while(st.tp>tp){
    del_tmp tmp=st.top();st.pop();
    if(!tmp.num)	continue;
    dsu.siz[dsu.fa[tmp.num]]-=tmp.siz;
    dsu.d[dsu.fa[tmp.num]]-=tmp.d;
    dsu.fa[tmp.num]=tmp.num;
  }
}

注意边权可能为 $0$。

Communication Towers

*2700

看见一个点只在某段时间出现，果断线段树分治。

通过可撤销并查集维护连通性。

这里涉及到一个新问题，也是线段树分治的一个trick：标记维护。

注意到需要给 $1$ 所在的树上的每个结点打上标记，这并不好办。

考虑只给树的根结点增加标记。在撤销操作（其实也是分裂子树）时下传标记。

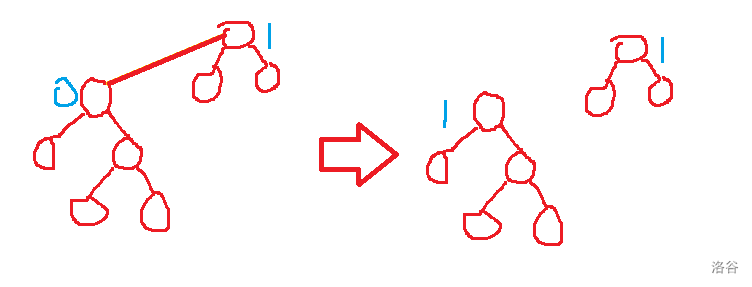
但这样会出现一种情况，一个子树后来连接上带有标记的根（但这个根现在不与 $1$ 相连），则会导致新的子树也被统计进入答案。

考虑一个解决方法，在连接时减去根的标记，撤销时加上。

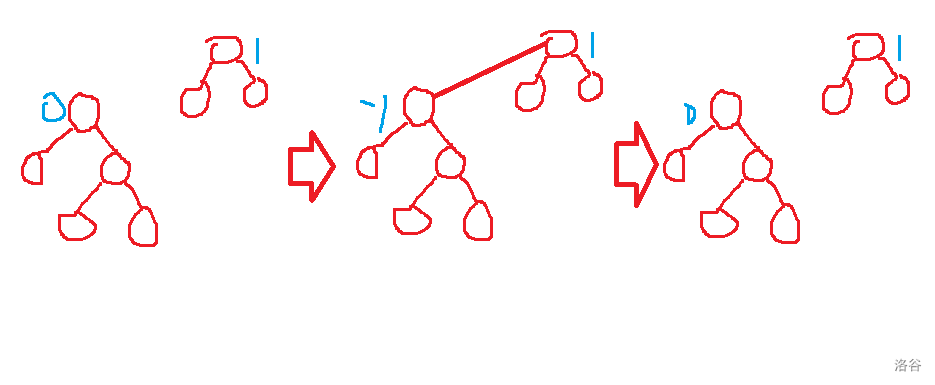
这样，只要根结点的标记在途中没有变化，就不会多下传。

//merge
del_tmp merge(int x,int y){
  int X=find(x),Y=find(y);
  if(X==Y)	return{0,0};
  if(d[X]>d[Y])	swap(X,Y);
  del_tmp ret={X,d[X]==d[Y]};
  d[Y]+=(d[X]==d[Y]),tag[X]-=tag[Y],fa[X]=Y;
  return ret;
}

//delete
while(st.tp>tp){
  del_tmp tmp=st.top();st.pop();
  if(!tmp.num)	continue;
  dsu.tag[tmp.num]+=dsu.tag[dsu.fa[tmp.num]];
  dsu.d[dsu.fa[tmp.num]]-=tmp.d;
  dsu.fa[tmp.num]=tmp.num;
}

下传标记的问题至此完美解决，剩的就是普通线段树分治的操作了。

code

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,mx,l[N],r[N],ans=0x3f3f3f3f;
template<typename T,int siz> struct my_stack{
	T st[siz];
	int tp=0;
	void push(T x){st[++tp]=x;}
	void pop(){
		if(!tp)	cerr<<"THE STACK IS EMPTY!\n";
		else	tp--;
	}
	T top(){
		if(!tp)	cerr<<"THE STACK IS EMPTY!\n";
		else	return st[tp];
	}
	void clear(){tp=0;}
	bool empty(){return !tp;}
};
struct del_tmp{int num,d;};
template<int N>struct DSU{
	int fa[N],tag[N],d[N];
	void clear(int n){for(int i=1;i<=n;i++)	fa[i]=i,tag[i]=0,d[i]=1;}
	int find(int x){return (fa[x]==x?x:find(fa[x]));}
	del_tmp merge(int x,int y){
		int X=find(x),Y=find(y);
		if(X==Y)	return{0,0};
		if(d[X]>d[Y])	swap(X,Y);
		del_tmp ret={X,d[X]==d[Y]};
		d[Y]+=(d[X]==d[Y]),tag[X]-=tag[Y],fa[X]=Y;
		return ret;
	}
	bool same(int x,int y){return find(x)==find(y);}
};
struct edge{int u,v;};
struct segment_tree{
	DSU<N> dsu;
	my_stack<del_tmp,N<<1>st;
	segment_tree(){dsu.clear(N-1);}
	struct segment_tree_node{vector<edge>v;}t[N<<2];
	inline int ls(int x){return x<<1;};
	inline int rs(int x){return x<<1|1;};
#define mid ((l+r)>>1)
	void change(int p,int l,int r,int re_l,int re_r,edge val){
		if(re_l<=l&&r<=re_r)	return t[p].v.push_back(val),void();
		else{
			if(re_l<=mid)	change(ls(p),l,mid,re_l,re_r,val);
			if(mid<re_r)	change(rs(p),mid+1,r,re_l,re_r,val);
		}
	}
	void query(int p,int l,int r){
		//		cerr<<p<<" "<<l<<" "<<r<<"\n";
		int tp=st.tp;
		for(auto it:t[p].v)	st.push(dsu.merge(it.u,it.v));
		if(l==r)	dsu.tag[dsu.find(1)]++;
		else	query(ls(p),l,mid),query(rs(p),mid+1,r);
		while(st.tp>tp){
			del_tmp tmp=st.top();st.pop();
			if(!tmp.num)	continue;
			dsu.tag[tmp.num]+=dsu.tag[dsu.fa[tmp.num]];
			dsu.d[dsu.fa[tmp.num]]-=tmp.d;
			dsu.fa[tmp.num]=tmp.num;
		}
	}
}T;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin>>n>>m;
	for(int i=1;i<=n;i++)	cin>>l[i]>>r[i],mx=max(mx,r[i]);
	for(int i=1,u,v;i<=m;i++){
		cin>>u>>v;
		if(max(l[u],l[v])<=min(r[u],r[v]))	T.change(1,1,mx,max(l[u],l[v]),min(r[u],r[v]),{u,v});
	}
	T.query(1,1,mx);
	for(int i=1;i<=n;i++){
		if(T.dsu.tag[i])	cout<<i<<" ";
	}
}

时间复杂度 $O(m\log{n}\log{R_{imax}})$。

Unique Occurrences

*2300

将同颜色的边去掉后，每条此颜色的边两边的连通块大小之积即为这条边的贡献。

线段树分治+可撤销并查集即可。

洞穴勘测

将操作与查询一起放进线段树里分治。递归到叶子结点时如果是询问就回答，不是就不管。

离线统计边的存在时间，每条边依次插入线段树即可。

query：

void query(int p,int l,int r){
  int tp=st.tp;
  for(auto it:t[p].v)	st.push(dsu.merge(it.u,it.v));
  if(l==r){
    if(q[l].u)	cout<<(dsu.same(q[l].u,q[l].v)?"Yes\n":"No\n");//有改变的地方
  }else	query(ls(p),l,mid),query(rs(p),mid+1,r);
  while(st.tp>tp){
    del_tmp tmp=st.top();st.pop();
    if(!tmp.num)	continue;
    dsu.d[dsu.fa[tmp.num]]-=tmp.d;
    dsu.fa[tmp.num]=tmp.num;
  }
}

add：

cin>>n>>m;
for(int i=1,u,v;i<=m;i++){
  cin>>s>>u>>v;
  if(u>v)	swap(u,v);
  if(s[0]=='C'){
    int tmp=ma[{u,v}];
    if(tmp)	la[tmp]=i;
    else	ma[{u,v}]=++cnt,e[cnt]={u,v},la[cnt]=i;
  }else if(s[0]=='D'){
    int tmp=ma[{u,v}];
    T.change(1,1,m,la[tmp],i-1,e[tmp]);
    la[tmp]=0;
  }else	q[i]={u,v};
}
for(int i=1;i<=cnt;i++)	if(la[i])	T.change(1,1,m,la[i],m,e[i]);

捉迷藏

问题变为了维护白点的直径，将每个点是白点的时间段插入线段树进行分治。当然你也可以用点分树。

直径的更新：
对于一个集合 $S$ 和只有一个点的集合 ${P}$。若集合 $S$ 的直径为 $(U,V)$。则点集 $S∩{P}$ 的直径只可能为 $(U,V)$，$(U,P)$ 或 $(V,P)$。

然后记录直径的两端点做到撤销，就可以线段树分治了。

A Museum Robbery

*2800

一件展品出现有时间限制，很明显的线段树分治。

看 $s(m)$ 的计算方式，大概就是线段树分治套背包了。

令 $dp_i$ 为总重量为 $i$ 时的最大价值，问题就转化为一个经典的 01 背包问题了。统计答案时做一个前缀和就可以了。

背包撤销时可以用退背包，也可以 $O(n)$ 记录修改之前的背包状态。我这里用的是后者。

code

#include<bits/stdc++.h>
using namespace std;
const long long N=1.5e4+5,M=3e4+5,W=1e3+5,p=1e7+19,mod=1e9+7;
int n,m,k,cnt,la[N];
long long power[W];
bool q[M];
struct exhabit{int c,w;}a[N];
struct segment_tree{
	int dp[W];
	struct segment_tree_node{vector<exhabit>v;}t[M<<2];
	inline int ls(int x){return x<<1;};
	inline int rs(int x){return x<<1|1;};
#define mid ((l+r)>>1)
	void change(int p,int l,int r,int re_l,int re_r,exhabit val){
		if(re_l<=l&&r<=re_r)	return t[p].v.push_back(val),void();
		else{
			if(re_l<=mid)	change(ls(p),l,mid,re_l,re_r,val);
			if(mid<re_r)	change(rs(p),mid+1,r,re_l,re_r,val);
		}
	}
	void query(int p,int l,int r){
		vector<int> pre(k+1,0);
		for(int i=1;i<=k;i++)	pre[i]=dp[i];
		for(auto it:t[p].v){
			for(int i=k;i>=it.w;i--)	dp[i]=max(dp[i],dp[i-it.w]+it.c);
		}
		if(l==r){
			if(q[l]){
				long long ma=-1,ans=0;
				for(int i=1;i<=k;i++){
					ma=max(ma,1ll*dp[i]);
					ans=(ans+ma*power[i-1]%mod)%mod;
				}
				cout<<ans<<"\n";
			}
		}else	query(ls(p),l,mid),query(rs(p),mid+1,r);
		for(int i=1;i<=k;i++)	dp[i]=pre[i];
	}
}T;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin>>n>>k;cnt=n;
	power[0]=1;
	for(int i=1;i<=k;i++)	power[i]=power[i-1]*p%mod;
	for(int i=1;i<=n;i++)	cin>>a[i].c>>a[i].w,la[i]=1;
	cin>>m;
	for(int i=1,opt,num;i<=m;i++){
		cin>>opt;
		if(opt==1){
			cnt++;
			cin>>a[cnt].c>>a[cnt].w;
			la[cnt]=i;
		}else if(opt==2){
			cin>>num;
			T.change(1,1,m,la[num],i,a[num]);
			la[num]=0;
		}else	q[i]=1;
	}
	for(int i=1;i<=cnt;i++){
		if(la[i])	T.change(1,1,m,la[i],m,a[i]);
	}
	T.query(1,1,m);
}

时间复杂度 $O((n+m)k\log{m}+km)$。

Painting Edges

*3300

真史登场。

发现 $k\le50$ 然而空间不足以开 $50$ 棵线段树，那就只能是一个线段树里面 $50$ 个并查集了。

先离线处理每条边颜色可能会更改的时间点（因为操作不合法时，颜色不会更改，所以不能直接插入），

然后线段树分治，在分治时分别添加各个颜色的边，如果有一个并查集不满足要求，整个子树都不合法。

回答完一个询问时，根据这个询问的信息获得边的颜色信息（即是否会更改），然后根据之前记录下的时间区间现场加到线段树后面去。

for(auto it:t[p].v){
	if(dsu[it.c].same(it.u,it.v)){
		ok=0;
		for(int i=l;i<=r;i++){
			cout<<"NO\n";
			if(e[Q[i].num].c&&i+1<nxt[i])	change(1,1,q,i+1,nxt[i]-1,e[Q[i].num]);
		}
		break;
	}
	st.push(dsu[it.c].merge(it.u+N,it.v));st.st[st.tp].c=it.c;
	st.push(dsu[it.c].merge(it.v+N,it.u));st.st[st.tp].c=it.c;
}
if(ok){
	if(l==r){
		cout<<"YES\n";
		e[Q[l].num].c=Q[l].c;
		if(l+1<nxt[l])	change(1,1,q,l+1,nxt[l]-1,e[Q[l].num]);
	}else	query(ls(p),l,mid),query(rs(p),mid+1,r);
}

其中 nxt 是下一次询问这条边的时间（如果没有下一次询问就是 $q+1$）。

需要注意的是，无论修改后是否合法，属于这个询问的叶子结点上加入的这条边一定是修改过后的颜色，因为你需要用修改过后的颜色去判断它合不合法。

for(int i=1;i<=q;i++){
	cin>>Q[i].num>>Q[i].c;
	nxt[last[Q[i].num]]=i,last[Q[i].num]=i;//辅助记录修改时间区间
	T.change(1,1,q,i,i,{e[Q[i].num].u,e[Q[i].num].v,Q[i].c});//强制加入修改后的颜色
}

代码实现部分完毕，但是这道题还卡空间。

tips1：如果你的做法里含有 STL 的 queue 并且数量为 $O(n)$ 级别。

请使用合理的方式或使用 queue<int,list<int>> 更换掉，否则定义 queue 的额外内存会让你MLE。

tips2: 请计算好需要使用的空间，尽量不要多开任何无意义的空间。

code

#include<bits/stdc++.h>
using namespace std;
const int N=500005;
int n,m,q,k;
template<typename T,int siz> struct my_stack{
	T st[siz];
	int tp=0;
	void push(T x){st[++tp]=x;}
	void pop(){
		if(!tp)	cerr<<"THE STACK IS EMPTY!\n";
		else	tp--;
	}
	T top(){
		if(!tp)	cerr<<"THE STACK IS EMPTY!\n";
		else	return st[tp];
	}
	void clear(){tp=0;}
	bool empty(){return !tp;}
};
struct del_tmp{int num,d;short int c;};
template<int N>struct DSU{
	int fa[N],d[N];
	void clear(int n){for(int i=1;i<=n;i++)	fa[i]=i,d[i]=1;}
	int find(int x){return (fa[x]==x?x:find(fa[x]));}
	del_tmp merge(int x,int y){
		int X=find(x),Y=find(y);
		if(d[X]>d[Y])	swap(X,Y);
		del_tmp ret={X,d[X]==d[Y],0};
		d[Y]+=(d[X]==d[Y]),fa[X]=Y;
		return ret;
	}
	bool same(int x,int y){return find(x)==find(y);}
};
struct edge{int u,v;short int c;}e[N];
struct query{int num;short int c;}Q[N];
int nxt[N],last[N];
struct segment_tree{
	DSU<N<<1> dsu[51];
	my_stack<del_tmp,N<<1>st;
	void clear(int k){for(int i=1;i<=k;i++)	dsu[i].clear((N<<1)-1);}
	struct segment_tree_node{vector<edge>v;}t[N<<2];
	inline int ls(int x){return x<<1;};
	inline int rs(int x){return x<<1|1;};
#define mid ((l+r)>>1)
	void change(int p,int l,int r,int re_l,int re_r,edge val){
		if(re_l<=l&&r<=re_r)	return t[p].v.push_back(val),void();
		else{
			if(re_l<=mid)	change(ls(p),l,mid,re_l,re_r,val);
			if(mid<re_r)	change(rs(p),mid+1,r,re_l,re_r,val);
		}
	}
	void query(int p,int l,int r){
		bool ok=1;int tp=st.tp;
		for(auto it:t[p].v){
			if(dsu[it.c].same(it.u,it.v)){
				ok=0;
				for(int i=l;i<=r;i++){
					cout<<"NO\n";
					if(e[Q[i].num].c&&i+1<nxt[i])	change(1,1,q,i+1,nxt[i]-1,e[Q[i].num]);
				}
				break;
			}
			st.push(dsu[it.c].merge(it.u+N,it.v));st.st[st.tp].c=it.c;
			st.push(dsu[it.c].merge(it.v+N,it.u));st.st[st.tp].c=it.c;
		}
		if(ok){
			if(l==r){
				cout<<"YES\n";
				e[Q[l].num].c=Q[l].c;
				if(l+1<nxt[l])	change(1,1,q,l+1,nxt[l]-1,e[Q[l].num]);
			}else	query(ls(p),l,mid),query(rs(p),mid+1,r);
		}
		while(st.tp>tp){
			del_tmp tmp=st.top();st.pop();
			dsu[tmp.c].d[dsu[tmp.c].fa[tmp.num]]-=tmp.d;
			dsu[tmp.c].fa[tmp.num]=tmp.num;
		}
	}
}T;
int main(){
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
	cin>>n>>m>>k>>q;
	for(int i=1;i<=m;i++)	cin>>e[i].u>>e[i].v;
	for(int i=1;i<=q;i++)	cin>>Q[i].num>>Q[i].c,nxt[last[Q[i].num]]=i,last[Q[i].num]=i,T.change(1,1,q,i,i,{e[Q[i].num].u,e[Q[i].num].v,Q[i].c});
	for(int i=1;i<=m;i++)	nxt[last[i]]=q+1;
	T.clear(k);
	T.query(1,1,q);
}

时间复杂度 $O(q\log{q}\log{n})$。

标签：tmp,int,线段,dsu,略解,st,num,杂题
From： https://www.cnblogs.com/mornstar/p/18459362

相关文章

  • 浅谈李超线段树
    众所周知，\(Li\Chao\Tree=LCT=Link\Cut\Tree\)。在我们的日常学习生活中，经常会遇到以下问题：维护一种数据结构，要求：添加一条线段求解\(x=k\)与所有线段交点中，\(y\)最大的一个。众所周知，线段会影响一个区间的答案。区间取\(max+\)单点最大值，想到线段树。但是该怎......
  • 浅谈一类动态开点线段树优化 - DEST树
    前言线段树，是一种优秀的数据结构，其应用极为广泛。其中，动态开点值域线段树，配合上线段树合并，甚至能替代或超越平衡树。但是，这种线段树的树高与值域相关，很容易产生四五倍常数。无论考虑时间或空间复杂度，这样的树都不算优。那么，我们是否能想办法优化它呢？优化思想正如上文所述，普通线......
  • 可持久化线段树
    可持久化线段树P3919【模板】可持久化线段树1（可持久化数组）维护一个长度为\(N\)的数组，支持如下几种操作在某个历史版本上修改某一个位置上的值访问某个历史版本上的某一位置的值此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新......
  • pakencamp 杂题选刷
    2023Day1GMST(Easy)\(\color{green}\checkmark\)给定序列\(a(|a_i|\le10^6)\)，构造\(n(n\le2\cdot10^5)\)个点的无向图，点\(i,j\)的边权是\(a_ia_j\)，求图的最小生成树。唐氏。首先给\(a\)排序，显然没有影响。考察\(a_i\ge0\)怎么做：显然答案就是\(a_1\c......
  • 李超线段树
    1问题李超线段树是线段树的一种变种，主要用于维护二维平面上的直线信息以及查询操作。它的应用范围很广，只要式子的形式能转化为一次函数就可以考虑使用李超线段树进行求解/优化。具体的，李超线段树支持下面两种操作：动态在平面中插入一条线段/直线。在平面上询问与一条直线......
  • 【笔记】杂题选讲 2024.10.5（DNF）
    十一杂题选讲-VirtualJudge(vjudge.net)/mnt/e/codes/contests/20241008/sol.md目录[AGC004F]Namori[1406E]DeletingNumbers[1081G]MergesortStrikesBack[1033E]HiddenBipartiteGraph[1254E]SendTreetoCharlie[1012E]Cyclesort[1284F]NewYearandSocialN......
  • 李超线段树
    最经典应用就是维护一个二维平面直角坐标系，支持动态插入线段（理解为有值域的一次函数\(y=kx+b\)），询问已插入线段与直线\(x=x_0\)交点的纵坐标最值。即当\(x=x_0\)，求\(max\)或\(min\){\(k_ix+b_i\)}对于普通求法的\(O(n)\)遍历，如何优化时间复杂度呢？其实就是找一种方......
  • B. 线段取交
    题目下载链接算法可以发现是求逆序对时间复杂度限制在\(O(n\logn)\)树状数组记录每一个值的多少转化为求前缀和#include<iostream>#include<cstdio>#include<algorithm>usingnamespacestd;inttree[500010],ranks[500010],n;longlongans;structpoint{......
  • 「杂题乱刷2」CF1372D
    题目链接CF1372DOmkarandCircle(*2100)解题思路发现问题等价于在环上砍一刀形成一个序列然后取其中不相邻的数字使得和最大。如果这是一个序列，我们只需要取奇数位上的数字和和偶数位上的数字和的最大值即可。我们发现你砍掉一刀等价于把后缀拿到最前面来。于是我们可以直......
  • 杂题选练
    一些杂题但可以记录下的。IP5300[GXOI/GZOI2019]与或和首先我们拆位，然后枚举每一个点\((i,j)\)，考虑将该点作为矩阵的右下角的贡献，先考虑\(AND\)，只有矩阵中的值都为\(1\)时才造成贡献，所以我们考虑记录\((i,j)\)左上方最大全为\(1\)的从左到右单调非严格递减的图形......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99