感觉非常有深度,感觉过几天就又要忘了,所以我写个题解。
P3806 【模板】点分治 1
给定一棵有 \(n\) 个点的树,询问树上距离为 \(k\) 的点对是否存在。
题意非常简单 题意越短越毒瘤。
我们先想想点对有几种情况:
第一种是经过根节点的路径;
第二种是不经过根节点的路径;
想第一种有路径距离 \(dis(u,v)=dis(u,root)+dis(v,root)\)。
而第二种呢,只是到了他们的另一个公共祖先,即另一个根,发现是不是有点分治的感觉了,大子树分为小子树,依次处理点对距离。


但是不做任何优化的话可能会有一个很深的子树,看大佬的图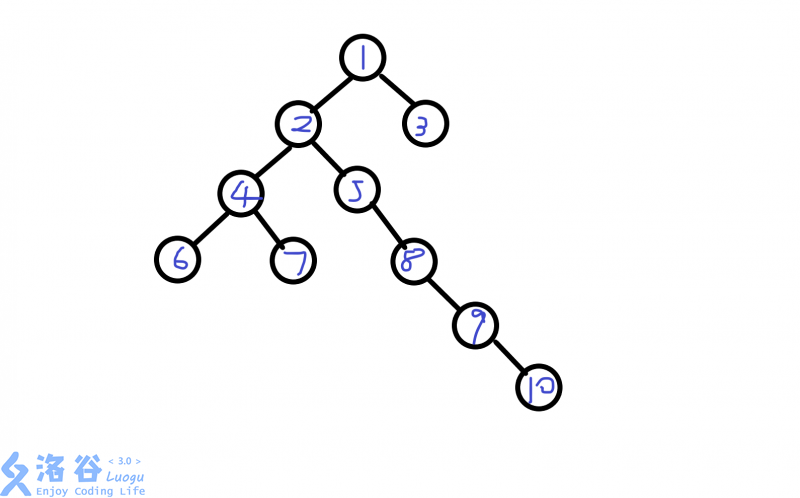
这时候依次处理就很慢了,此时我们就要找到重心(删掉重心后剩下的子树尽可能地平衡(分出来的最大子树的size尽可能地小))
然后就没了,反复找重心,处理距离就可以了,然后我就讲下代码如何实现吧。
找重心,找树中的每个点,找到一个节点最大子树所拥有的节点数尽可能小。
void getroot(int x,int f){
siz[x]=1;//树大小
dp[x]=0;//最大的子树
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]||y==f){//不能是父节点
continue;
}
getroot(y,x);//遍历子节点
siz[x]+=siz[y];//更新大小
dp[x]=max(dp[x],siz[y]);//最大子树的大小
}
dp[x]=max(dp[x],sum-siz[x]);//父节点的子树大小也算
if(dp[x]<dp[root]){//最大的子树更小,更新重心为根
root=x;
}
}
我们找到了个根,想知道到所以点的距离怎么办,计算!!!
void getdis(int x,int f){
rev[++tot]=dis[x];//有这么一个距离(记住了)
if(dis[x]>1e7){//洛谷机制路径太大不合法
return
}
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]||y==f){
continue;
}
dis[y]=dis[x]+e[i].w;//更新距离
getdis(y,x);//更新距离
}
}
此时知道根到每个点的距离,那该处理答案了吧。
void doit(int x){
int c=0;//记录有多少个距离
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]){
continue;
}
tot=0;//有几个路径
dis[y]=e[i].w;//更新距离
getdis(y,x);
for(int j=1;j<=tot;j++){
for(int k=1;k<=m;k++){//遍历询问
if(query[k]>=rev[j]){
pax[k]|=pd[query[k]-rev[j]];//如果有这么个值更新
}
}
}
for(int j=1;j<=tot;j++){
pd[rev[j]]=1;//表示有这么个值
q[++c]=rev[j];//为了清除
}
}
for(int i=1;i<=c;i++){
pd[q[i]]=0;//清除,优化时间
}
}
此时该向下递归根节点了。
void solve(int x){
vis[x]=1,pd[0]=1;
doit(x);//处理当x为根,所有点对的距离
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]){
continue;
}
sum=siz[y];//设子树大小
root=0;//更新子树重心
getroot(y,x);//找新子树的重心
solve(root);
}
}
好了上面就是主要的代码了,你应该蒙了吧,确实会晕的,但菜就多练。
点击查看完整代码
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e7+10;
#define int ll
int n,m;
struct ss{
int v,w,next;
}e[N];
int cnt=2,head[N];
void add(int u,int v,int w){
e[cnt].v=v;
e[cnt].w=w;
e[cnt].next=head[u];
head[u]=cnt++;
}
int query[N];
int vis[N],siz[N],root,dp[N],sum,pd[N];
int rev[N],q[N],dis[N],pax[N];
void getroot(int x,int f){
siz[x]=1;
dp[x]=0;
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]||y==f){
continue;
}
getroot(y,x);
siz[x]+=siz[y];
dp[x]=max(dp[x],siz[y]);//最大子树的大小
}
dp[x]=max(dp[x],sum-siz[x]);//父节点的子树大小也算
if(dp[x]<dp[root]){//找子树最小
root=x;
}
}
int tot=0;
void getdis(int x,int f){
rev[++tot]=dis[x];//记录距离
if(dis[x]>1e7){
return
}
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]||y==f){
continue;
}
dis[y]=dis[x]+e[i].w;//更新距离
getdis(y,x);
}
}
void doit(int x){
int c=0;
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]){
continue;
}
tot=0;
dis[y]=e[i].w;
getdis(y,x);
for(int j=1;j<=tot;j++){
for(int k=1;k<=m;k++){
if(query[k]>=rev[j]){
pax[k]|=pd[query[k]-rev[j]];
}
}
}
for(int j=1;j<=tot;j++){
pd[rev[j]]=1;
q[++c]=rev[j];
}
}
for(int i=1;i<=c;i++){
pd[q[i]]=0;
}
}
void solve(int x){
vis[x]=1,pd[0]=1;
doit(x);//处理当x为根,所有点对的距离
for(int i=head[x];i;i=e[i].next){
int y=e[i].v;
if(vis[y]){
continue;
}
//dp[0]=n;
sum=siz[y];//设子树大小
root=0;//更新子树重心
getroot(y,x);
solve(root);
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
for(int i=1;i<=n-1;i++){
getroot(1,0);
solve(root);
for(int i=1;i<=m;i++){
if(pax[i]){
cout<<"AYE\n";
}
else{
cout<<"NAY\n";
}
}
return 0;
}