一、DFS(离散傅里叶级数)
function y= DFS(x,L)
N = length(x);
xi=[x;zeros(L-N,1)];
y = zeros(1, L);
for k = 1:L
sum = 0;
for n = 1:L
sum = sum + xi(n) * exp(-2j*pi*k*n/L);
end
y(k) = sum;
end
end
二、DFT(离散傅里叶变换)
function y= DFT(x,L)
N = length(x);
xi=[x;zeros(L-N,1)];
y = zeros(1, L);
for k = 1:L
sum = 0;
for n = 1:L
sum = sum + xi(n) * exp(-2j*pi*k*n/L);
end
y(k) = sum;
end
end
三、DTFT(离散时间傅立叶变换)
function y1 = DTFT(x, w)
N = length(x);
y1 = zeros(size(w));
for k = 1:length(w)
sum = 0;
for n = 1:N
sum = sum + x(n)*exp(-1j*n*w(k));
end
y1(k) = sum;
end
end
四、比较
N=256;
n=0:N-1;
k=10;
L=256
x=sin(2*pi*k*n/N);
y=DFT(x,L);
w=linspace(-pi,pi,512);
y1=DTFT(x,w);
figure;
subplot(2,1,1);
stem(0:N-1,abs(y),'filled');
subplot(2,1,2);
plot(w,abs(y1));
(DFS和DFT类似,只是DFS是DFT的延拓,DFT是DFS的主值序列,这里只比较了DTFT和DFT的关系)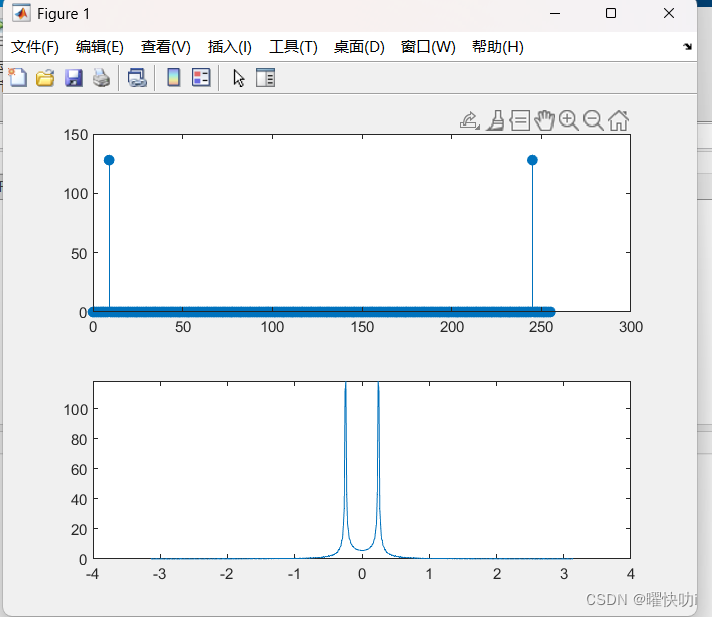
DFT中间区域基本全是零是由于信号x的能量主要集中在少数几个频率点上,而这些非峰值位置的DFT值非常小,在视觉上可能看起来像0。而DTFT由于连续性,能更好地展示信号的频域特性。
标签:end,自定义,DFT,sum,DFS,y1,DTFT From: https://blog.csdn.net/weixin_73825075/article/details/142765930