无耻的广告更好的阅读体验~
最近在搞个人博客博客园的差点忘了更了。
已经沦落到在写这种水题题解了。
题目翻译
有 \(n\) 队人,每个队人数不同,把他们分成 2 组(同一队的不能拆开),使两组人数差距尽量小。
形式化题意:有 \(n\) 个数,把它们分成两组,使两组和的差尽量小。
说句闲话:感觉这题目很经典,但我没有原题作为证据(大雾
解法
本来觉得我这菜鸡实力是不可能做出来的,已经准备摆烂了,此时我突然发现 \(n \le 20\)。
这是啥概念?
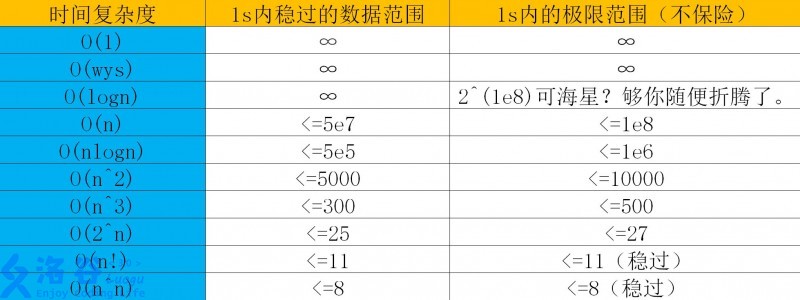
看图,\(n \le 25\) 都是可以用 \(O(2 ^ n)\) 做法解决的,这不结束了?直接枚举每一组,分类讨论是 A 组还是 B 组,就可以了。
给个小建议:可以记录总人数,这样子只需要记录 A 组人数,B 组人数可以直接 \(O(1)\) 计算,这样就变成选与不选的 dfs 模板题目了……更关键的是这样子不需要记录为每一队对应哪一组了。
代码
ACCode with 注释
/*Code by Leo2011*/
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f
#define EPS 1e-8
#define FOR(i, l, r) for (int(i) = (l); (i) <= (r); ++(i))
#define log printf
#define IOS \
ios::sync_with_stdio(false); \
cin.tie(nullptr); \
cout.tie(nullptr);
using namespace std;
typedef __int128 i128;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 30;
int n, a[N], ans = INF, sum;
template <typename T>
inline T read() {
T sum = 0, fl = 1;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') fl = -1;
for (; isdigit(ch); ch = getchar()) sum = sum * 10 + ch - '0';
return sum * fl;
}
template <typename T>
inline void write(T x) {
if (x < 0) {
putchar('-'), write<T>(-x);
return;
}
static T sta[35];
int top = 0;
do { sta[top++] = x % 10, x /= 10; } while (x);
while (top) putchar(sta[--top] + 48);
}
void dfs(int group, int cnt) {
if (group == n) {
ans = min(ans, max(cnt, sum - cnt));
return;
}
// 组 A
dfs(group + 1, cnt + a[group]);
// 组 B
dfs(group + 1, cnt);
}
int main() {
n = read<int>();
FOR(i, 1, n) a[i] = read<int>(), sum += a[i];
dfs(1, 0);
write<int>(ans);
return 0;
}
// 20组---》爆搜挂着机,打表出 AC
理解万岁!
标签:cnt,ch,group,int,题解,sum,dfs,Lunch,abc374 From: https://www.cnblogs.com/leo2011/p/18449796