吾日三省吾身：末日时在干什么？有没有空？可以来拯救一下吗？

算法思想

非常简单：就是暴力。

对于数据结构题，我们有这样一种思路去维护：对于一个数列，我们把不同的数字看成不同的颜色段，然后对每个颜色段进行暴力操作，可以有效降低时间复杂度。但这种暴力是很好卡掉的，只需让颜色段尽可能多，算法就可以直接退化的 \(O(n^2)\)，甚至在随机数据下，这种算法的表现依然不是很好。

但在特定的情况下，当题目中的颜色段很少（例如：存在区间赋值操作且数据随机），这种算法就可以达到 \(O(n\log n)\) 等极好的时间复杂度，珂朵莉树，也叫老司机树（英文：Old Drive Tree，简写：ODT）应运而生。可以支持许多复杂的操作。

算法讲解

模板：CF896C Willem, Chtholly and Seniorious

题意简述：

写一个数据结构，支持以下操作：

1 l r x：将\([l,r]\) 区间所有数加上\(x\)
2 l r x ：将\([l,r]\) 区间所有数改成\(x\)
3 l r x ：输出将\([l,r]\) 区间从小到大排序后的第\(x\) 个数是的多少（即区间第\(x\) 小，数字大小相同算多次，保证 \(1\leq\) \(x\) \(\leq\) \(r-l+1\)）
4 l r x y ：输出\([l,r]\) 区间每个数字的\(x\) 次方的和模\(y\) 的值，即\(\left(\sum^r_{i=l}a_i^x\right)\)\(\bmod y\)。

操作用普通的数据结构难以维护，同时存在区间赋值操作，启发我们使用珂朵莉树。

珂朵莉树实际上就是一个 set，set 中的每个节点都是一个颜色段。

struct cht{
	int l,r;
	mutable ll v;//用于快速修改颜色
	cht(int L,int R,ll V){
		l=L,r=R,v=V;
	}
	bool operator < (const cht &a)const {
		return l<a.l;
	}//默认按照颜色段左端点排序
};
typedef set<cht>::iterator iter;//迭代器，就是指针，接下来的各种操作都会常用
set<cht>s;

操作 \(1\)：split

这是珂朵莉树中最为重要的操作之一。

我们定义 split(pos) 表示返回以 \(pos\) 为左端点的颜色段的指针。特别的，如果 \(pos\) 位于颜色段 \(l,r\) 内，并非是端点，则将 \([l,r]\) 分裂为 \([l,pos-1],[pos,r]\) 并返回后者的指针；如果不存在 \(pos\) 这个位置，则返回 set 的尾指针。

步骤其实十分简单：

找到 \(pos\) 所在颜色段。
如果 \(pos\) 是该颜色段的端点，直接返回指针
分裂，返回分裂后的结果

iter split(int pos){
	iter it=s.lower_bound(cht{pos,0,0});//查找颜色段
	if(it!=s.end()&&it->l==pos)return it;//判断是否是端点，前面的特判是为了避免不存在 pos 导致 RE
	it--;//此时的 it 指向的颜色段包含 pos
	if(it->r<pos)return s.end();//特判 pos 是否存在
	int L=it->l,R=it->r;ll V=it->v;
	s.erase(it);//分裂
	s.insert(cht{L,pos-1,V});
	return s.insert(cht{pos,R,V}).first; //insert 返回的 pair 的第一个参数是新插入的位置的迭代器
}

操作 \(2\)：assign

区间推平，同样也是极其重要的操作之一。

我们要做的就是先分裂出以 \(l,r\) 为端点的颜色段，记为 \(s,t\)，然后将编号 \([s,t)\) 以内的所有颜色段删除，然后再插入一个以 \([l,r]\) 为端点的大颜色段。

set 支持删掉某个范围内的所有元素，调用 erase(s,t) 即可删除 set 中所有位于 \([s,t)\) 的元素。

void assign(int l,int r,ll k){
	iter itr=split(r+1),itl=split(l);//r+1 是因为 erase 函数遵循左闭右开原则
	s.erase(itl,itr);
	s.insert(cht{l,r,k});  
}

注意到我们先调用了 split(r+1) 后再调用了 split(l)。这个顺序是不可改变的。因为具体解释比较麻烦，所以我盗了一张大佬的图（by user43206）

原因图

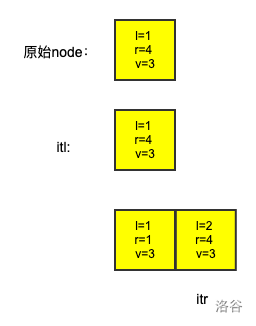
注意到调用 split(l) 后再调用 split(r+1) 可能会导致 \(itl\) 原本指向的颜色段被删除分裂成两个，所以我们必须按照正确的顺序分裂。

其他操作

其实非常简单，就是分裂出左右颜色段，然后暴力遍历其中的所有颜色段.....

是的，就是这么简单，给出一份伪代码

change(int l,int r,...){
    iter itr=split(r+1),itl=split(l);
	for(iter it=itl;it!=itr;it++){
		/*
        do something
        */
	}
    /*
    do something
    */
}

区间加

void add(int l,int r,ll k){
	iter itr=split(r+1),itl=split(l);
	for(iter it=itl;it!=itr;it++){
		it->v+=k;//可以直接改变结构体的成员是因为使用了 mutable
	}
	return;
}

区间第 \(k\) 小

#define pli pair<ll,int>
#define mp make_pair
typedef long long ll;
pli bk[N];
int tot;
ll kth(int l,int r,int rk){
	tot=0;
	iter itr=split(r+1),itl=split(l);
	for(iter it=itl;it!=itr;it++){
		bk[++tot]=mp(it->v,it->r-it->l+1);
	} 
	sort(bk+1,bk+1+tot);
	for(int i=1;i<=tot;i++){
		if(rk<=bk[i].second)return bk[i].first;
		rk-=bk[i].second;
	}
    return -1;
}

区间幂的和

ll ksm(ll a,ll b,ll p){
	ll ans=1;
	while(b){
		if(b&1)ans=(ans*a)%p;
		a=(a*a)%p;
		b>>=1;
	}
	return ans;
}
ll pow_sum(int l,int r,ll x,ll y){
	iter itr=split(r+1),itl=split(l);
	ll res=0;
	for(iter it=itl;it!=itr;it++){
		res+=(it->r-it->l+1)*ksm(it->v%y,x,y)%y;
        res%=y;
	} 
    return res;
}

然后这题就做完了，提交记录。

时间复杂度

不会证，但是是神奇的 \(O(n\log n)\)。

例题

鸽，以后补几道。

The End

「最喜欢珂朵莉了」

标签：itl,int,ll,pos,iter,朵莉树,split
From： https://www.cnblogs.com/zuoqingyuan114/p/18447399

珂朵莉树