首页 > 其他分享 >洛谷 CF896C Willem, Chtholly and Seniorious之珂朵莉树板子

洛谷 CF896C Willem, Chtholly and Seniorious之珂朵莉树板子

时间：2024-08-10 12:54:47浏览次数：5  
标签：Willem Chtholly itl 之珂朵莉树 ll split Downarrow itr mod

洛谷CF896C题解

传送锚点

摸鱼环节

Willem, Chtholly and Seniorious

题面翻译

【题面】
请你写一种奇怪的数据结构，支持：

  • \(1\) \(l\) \(r\) \(x\) ：将\([l,r]\) 区间所有数加上\(x\)
  • \(2\) \(l\) \(r\) \(x\) ：将\([l,r]\) 区间所有数改成\(x\)
  • \(3\) \(l\) \(r\) \(x\) ：输出将\([l,r]\) 区间从小到大排序后的第\(x\) 个数是的多少(即区间第\(x\) 小，数字大小相同算多次，保证 \(1\leq\) \(x\) \(\leq\) \(r-l+1\) )
  • \(4\) \(l\) \(r\) \(x\) \(y\) ：输出\([l,r]\) 区间每个数字的\(x\) 次方的和模\(y\) 的值(即(\(\sum^r_{i=l}a_i^x\) ) \(\mod y\) )

【输入格式】
这道题目的输入格式比较特殊，需要选手通过\(seed\) 自己生成输入数据。
输入一行四个整数\(n,m,seed,v_{max}\) （$1\leq $ \(n,m\leq 10^{5}\) ,\(0\leq seed \leq 10^{9}+7\) $,1\leq vmax \leq 10^{9} $ ）
其中\(n\) 表示数列长度，\(m\) 表示操作次数，后面两个用于生成输入数据。
数据生成的伪代码如下

其中上面的op指题面中提到的四个操作。

【输出格式】
对于每个操作3和4，输出一行仅一个数。

题目描述

— Willem...

— What's the matter?

— It seems that there's something wrong with Seniorious...

— I'll have a look...

Seniorious is made by linking special talismans in particular order.

After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.

Seniorious has $ n $ pieces of talisman. Willem puts them in a line, the $ i $ -th of which is an integer $ a_{i} $ .

In order to maintain it, Willem needs to perform $ m $ operations.

There are four types of operations:

  • $ 1\ l\ r\ x $ : For each $ i $ such that $ l<=i<=r $ , assign $ a_{i}+x $ to $ a_{i} $ .
  • $ 2\ l\ r\ x $ : For each $ i $ such that $ l<=i<=r $ , assign $ x $ to $ a_{i} $ .
  • $ 3\ l\ r\ x $ : Print the $ x $ -th smallest number in the index range $ [l,r] $ , i.e. the element at the $ x $ -th position if all the elements $ a_{i} $ such that $ l<=i<=r $ are taken and sorted into an array of non-decreasing integers. It's guaranteed that $ 1<=x<=r-l+1 $ .
  • $ 4\ l\ r\ x\ y $ : Print the sum of the $ x $ -th power of $ a_{i} $ such that $ l<=i<=r $ , modulo $ y $ , i.e. .

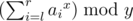输入格式

The only line contains four integers $ n,m,seed,v_{max} $ ( $ 1<=n,m<=10{5},0<=seed<10+7,1<=vmax<=10^{9} $ ).

The initial values and operations are generated using following pseudo code:

def rnd():

    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:

    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:

    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r): 
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

Here $ op $ is the type of the operation mentioned in the legend.

输出格式

For each operation of types $ 3 $ or $ 4 $ , output a line containing the answer.

样例 #1

样例输入 #1

10 10 7 9

样例输出 #1

2
1
0
3

样例 #2

样例输入 #2

10 10 9 9

样例输出 #2

1
1
3
3

提示

In the first example, the initial array is $ {8,9,7,2,3,1,5,6,4,8} $ .

The operations are:

  • $ 2\ 6\ 7\ 9 $
  • $ 1\ 3\ 10\ 8 $
  • $ 4\ 4\ 6\ 2\ 4 $
  • $ 1\ 4\ 5\ 8 $
  • $ 2\ 1\ 7\ 1 $
  • $ 4\ 7\ 9\ 4\ 4 $
  • $ 1\ 2\ 7\ 9 $
  • $ 4\ 5\ 8\ 1\ 1 $
  • $ 2\ 5\ 7\ 5 $
  • $ 4\ 3\ 10\ 8\ 5 $

一股浓浓的二次元oier味，是的，这是珂朵莉树的模板。

正片开始

珂朵莉树用于在数据随机的情况下处理区间平铺问题非常给力，可以用堆维护，结构体储存信息。

#define IT set<node>::iterator

1.维护信息

用结构体维护珂朵莉树各区间的信息。

code：

struct node
{
    ll l,r;
    mutable ll v;
    node(ll l,ll r=0,ll v=0):l(l),r(r),v(v){}
    bool operator<(const node &o) const
    {
        return l<o.l;
    }
};

2.关键 · 分离操作

利用指针将树的区间进行分割，此时分成三种情况，具体实现见代码。

code：

IT split(int pos)
{
    IT it=s.lower_bound(node(pos));//获得指针
    if(it!=s.end()&&it->l==pos) return it;//如果指针在开头，则直接返回
    it--;
    if(it->r<pos) return s.end();//pos过大，返回end
    ll l=it->l,r=it->r,v=it->v;
    s.erase(it);//清空原位置 
    s.insert(node(l,pos-1,v));//更新
    return s.insert(node(pos,r,v)).first;
}

2.区间增加

用指针指向区间左右端，对区间值增加即可。

code：

void add(ll l,ll r,ll val)
{
    IT itr=split(r+1),itl=split(l);//寻找左右端点
    for(IT it=itl;it!=itr;++it) it->v+=val;
}

3.区间铺平

分离后清空，直接搞。

code：

void assign_val(ll l,ll r,ll val)
{
    IT itr=split(r+1),itl=split(l);
    s.erase(itl,itr);//清空区间
    s.insert(node(l,r,val));//覆盖修改
}

4.查询区间第k小。

缓存下区间，排完序后直接搞。

code：

struct RANK
{
    ll num,cnt;
    bool operator<(const RANK &a) const
    {
        return num<a.num;
    }
    RANK(ll num,ll cnt):num(num),cnt(cnt){}
};//缓存信息
ll ranks(ll l,ll r,ll k)
{
    IT itr=split(r+1),itl=split(l);
    vector<RANK> vp;
    for(IT i=itl;i!=itr;++i)
    {
        vp.push_back(RANK(i->v,i->r - i->l+1));
    }
    sort(vp.begin(),vp.end());//排序找第k小
    int i;
    for(i=0;i<vp.size();++i)
    {
        if(vp[i].cnt<k)
        {
            k-=vp[i].cnt;
        }
        else {break;}
    }
    return vp[i].num;
}

5.区间数字\(x\)次方和。

很明显得用快速幂。

code：

ll pown(ll a,ll b,ll mod)
{
    ll res=1;
    ll ans=a%mod;
    while(b)
    {
        if(b&1) {res=res*ans%mod;}
        ans=ans*ans%mod;
        b>>=1;
    }
    return res;
}

暴力枚举区间值，把区间丢入快速幂，后乘区间长度，并统计答案即可。

code：

ll sum(ll l,ll r,ll e,ll mod)
{
    IT itr=split(r+1),itl=split(l);
    ll res=0;
    for(IT i=itl;i!=itr;++i)
        res=(res+pown(i->v,e,mod)*(i->r - i->l+1)%mod)%mod;//利用快速幂计算区间数值的x次方并乘上区间长度，再相加
    return res;
}

注意 · 注意！！！

在进行分离操作时，一定要先右后左，如果先处理\(itl\)，再处理\(itr\)时，原指向\(itl\)的地方会被清空掉，此时再调用s.erase就会RE。

同时由于数据随机，所以RE是概率发生，此时就是RP大比拼时刻了.

完整代码

#include<bits/stdc++.h>
#define IT set<node>::iterator
using namespace std;
typedef long long ll;
const ll MOD= 1e9+7;
const ll N=1e5+5;

struct node
{
    ll l,r;
    mutable ll v;
    node(ll l,ll r=0,ll v=0):l(l),r(r),v(v){}
    bool operator<(const node &o) const
    {
        return l<o.l;
    }
};
ll n,m,seed,vmax,a[N];
set<node>s;
IT split(int pos)
{
    IT it=s.lower_bound(node(pos));
    if(it!=s.end()&&it->l==pos) return it;
    it--;
    if(it->r<pos) return s.end();
    ll l=it->l,r=it->r,v=it->v;
    s.erase(it);
    s.insert(node(l,pos-1,v));
    return s.insert(node(pos,r,v)).first;
}
void add(ll l,ll r,ll val)
{
    IT itr=split(r+1),itl=split(l);
    for(IT it=itl;it!=itr;++it) it->v+=val;
}
void assign_val(ll l,ll r,ll val)
{
    IT itr=split(r+1),itl=split(l);
    s.erase(itl,itr);
    s.insert(node(l,r,val));
}
struct RANK
{
    ll num,cnt;
    bool operator<(const RANK &a) const
    {
        return num<a.num;
    }
    RANK(ll num,ll cnt):num(num),cnt(cnt){}
};
ll ranks(ll l,ll r,ll k)
{
    IT itr=split(r+1),itl=split(l);
    vector<RANK> vp;
    for(IT i=itl;i!=itr;++i)
    {
        vp.push_back(RANK(i->v,i->r - i->l+1));
    }
    sort(vp.begin(),vp.end());
    int i;
    for(i=0;i<vp.size();++i)
    {
        if(vp[i].cnt<k)
        {
            k-=vp[i].cnt;
        }
        else {break;}
    }
    return vp[i].num;
}
ll pown(ll a,ll b,ll mod)
{
    ll res=1;
    ll ans=a%mod;
    while(b)
    {
        if(b&1) {res=res*ans%mod;}
        ans=ans*ans%mod;
        b>>=1;
    }
    return res;
}
ll sum(ll l,ll r,ll e,ll mod)
{
    IT itr=split(r+1),itl=split(l);
    ll res=0;
    for(IT i=itl;i!=itr;++i)
        res=(res+pown(i->v,e,mod)*(i->r - i->l+1)%mod)%mod;
    return res;
}
ll rnd()
{
    ll ret=seed;
    seed=(seed*7+13)%MOD;
    return ret;

}
int main()
{
    cin>>n>>m>>seed>>vmax;
    for(int i=1;i<=n;++i)
    {
        a[i]=(rnd()%vmax)+1;
        s.insert(node(i,i,a[i]));
    }
    for(ll i=1;i<=m;++i)
    {
        ll op,l,r,x,y;
        op=(rnd()%4)+1;
        l=(rnd()%n)+1;
        r=(rnd()%n)+1;
        if(l>r) swap(l,r);
        if(op==3){
            x=(rnd()%(r-l+1))+1;
        }
        else{
            x=(rnd()%vmax)+1;
        }
        if(op==4) {
            y=(rnd()%vmax)+1;
        }


        if(op==1) add(l,r,x);
        else if(op==2) assign_val(l,r,x);
        else if(op==3) cout<<ranks(l,r,x)<<endl;
        else cout<<sum(l,r,x,y)<<endl;
    }
    return 0;
}

完结收工！！！！！

个人主页

看完点赞，养成习惯

\(\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\)

标签：Willem,Chtholly,itl,之珂朵莉树,ll,split,Downarrow,itr,mod
From： https://www.cnblogs.com/qc0817/p/18352184

相关文章

  • CF896C Willem, Chtholly and Seniorious 题解
    题目链接：CF或者洛谷比较经典的题目看到存在随机数据以及区间赋值先别急，我们发现第四个操作是很难办的，第四个操作貌似只有暴力才好做。这个时候我们可以考虑使用珂朵莉树来做，这题也是珂朵莉树的出处。使用平衡树去写珂朵莉树的话，那么随机数据下，连续段的期望为\(\log{n}\)个，所......
  • CF896C Willem, Chtholly and Seniorious
    题意维护一个序列\(s\)，有以下操作。区间加。区间覆盖。求\(l\)到\(r\)的第\(k\)小元素。求\(l\)到\(r\)的每个元素的\(x\)次方之和膜\(y\)。输入由给定种子随机生成。Sol珂朵莉树。本质上就是拿\(set\)乱搞。考虑每次操作对于颜色段的影响。每次操......
  • P3933 Chtholly Nota Seniorious
    原题是一个完全不困难的题，但里面一个性质没有想到QwQ性质：最大值一定在两个部分之一(显然)于是我们二分答案后，\(O(n^2)\)的找到从左下角开始包含最大值且极差\(\leqx\)的所能覆盖的最大区域，然后判断另一个区域极差是否\(\leqx\)即可不一定从左下角开始？旋转\(4\)次做\(4\)次即......
  • CF896B Ithea Plays With Chtholly
    原题翻译Chtholly可爱捏我们先考虑如果\(n\cdotc\leqm\)我们要怎么做，我们可以发现里面一定存在一个数出现了\(\geq\lceil\frac{m}{c}\rceil\)，不妨设这个数为\(x\)，因此我们只需要把所有数都改成\(x\)就可以了等等好像不对，我们一开始并不知道这个数是什么，我们只能一个一......
  • CF896E/洛谷 P4117 [Ynoi2018]五彩斑斓的世界/Welcome home, Chtholly
    分块。我们先来考虑修改对整块的影响。记值域为\(V=10^5\)。考虑对每一块维护\(V\)个集合\(S_1,S_2,\cdots,S_V\)，第\(i\)个集合\(S_i\)维护了区间中所有\(=i\)的元素的一些信息，并维护区间的最大值\(m\)，对于一次操作\(x\)：若\(m\le2x\)，我们暴力对每个\(i\in[x+1,......
  • Codeforces Round #449 (Div. 1) C Willem, Chtholly and Seniorious
    Willem,ChthollyandSeniorious珂朵莉树慕名而来操作\(3\)直接排序是我没想到的，因为随机数据所以才能过吧\(split\)操作中忘了开\(longlong\)，\(wa3\)#include<......
  • Codeforces897B-Chtholly's request
    B.Chtholly'srequesttimelimitpertestmemorylimitpertestinputoutput—Thanksalotfortoday.—Iexperien......
  • Willemijn 如何将职业生涯从营销转向 Web 开发和网络安全
    Willemijn如何将职业生涯从营销转向Web开发和网络安全转行是个人发展的重要一步。但是两次转换职业需要巨大的热情和承诺。这正是我们的毕业生WillemijnWaterbolk......
  • CF896C Willem, Chtholly and Seniorious
    写一种数据结构，支持：\(1\)\(l\)\(r\)\(x\)：将\([l,r]\)区间所有数加上\(x\)\(2\)\(l\)\(r\)\(x\)：将\([l,r]\)区间所有数改成\(x\)\(3\)\(l\)\(r\)\(x\)：输......
  • CF896E Welcome home, Chtholly
    题面维护一个\(n(n\leqslant100000)\)个元素序列\(a_1,a_2,\dots,a_n\)，有\(m(m\leqslant100000)\)次操作，分为如下两种。给定\(l,r,x\)，将\(a_l,a_{l+1},\dots,a_r\)中......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99