(一)
二分套二分。(感觉是一个很麻烦的做法。)
题目问的是让额外给的票最少,考虑二分答案。
设二分的答案为 \(x\),该候选人原来的得票为 \(v\),想要超过他至少要 \(x+v+1\)。
同时用前缀和维护区间和。
第一种情况为该候选人在前 \(m\) 个人中,如下图所示。
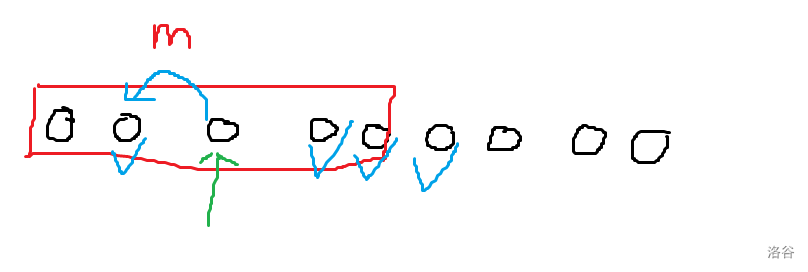
绿色箭头为被讨论的人,蓝色箭头表示 \(x+v+1\) 在原数组中的位置,蓝勾的则是最劣情况下超过当前候选人的人。
可以计算出蓝勾位置原来的和与最劣下和的差,是否够分配。
蓝色箭头指向位置可以二分。(其实是我不会 lower_bound。)
第二种情况是当前候选人不在前 \(m\) 位,那么无脑选前 \(m\) 中小于 \(x+v+1\) 的即可。
其实两种情况相差不大,但赛时代码又臭又长。
特别鸣谢:Daniel234 在赛时的口头鼓励,虽然毫无用处,但他与 *1300 斗智斗勇始终印象深刻。
(二)
AC 代码。
// LUOGU_RID: 179341441
//2024-09-28 20:13:53
#include<bits/stdc++.h>
#define db double
#define pb push_back
#define eb emplace_back
#define fi first
#define se second
#define mkp make_pair
#define pii pair<int,int>
#define int long long
using namespace std;
bool MBE;
inline int read(){
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-f;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int mxn=2e5+10;
int ans[mxn],s,n,m,k,sum[mxn];
struct node{
int val,pos;
}a[mxn];
bool cmp(node x,node y){
return x.val>y.val;
}
int query1(int pos,int x){
int t=a[pos].val+x+1,p=k-x,ss;
int l=1,r=m+1,ans=1;
while(l<=r){
int mid=(l+r)>>1;
if(a[mid].val<=t)ans=mid,r=mid-1;
else l=mid+1;
}
if(ans==pos){
ans++;
ss=sum[m+1]-sum[ans-1];
return (k-x)<t*(m-ans+2)-ss;
}
ss=sum[m+1]-sum[ans-1]-a[pos].val;
return (k-x)<t*(m-ans+1)-ss;
}
int query2(int pos,int x){
if(a[pos].val+x<a[m].val)return 0;
int l=1,r=m,ans=1,p=a[pos].val+x+1;
while(l<=r){
int mid=(l+r)>>1;
if(a[mid].val<=p)ans=mid,r=mid-1;
else l=mid+1;
}
int ss=sum[m]-sum[ans-1];
return (k-x)<p*(m-ans+1)-ss;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
n=read(),m=read(),k=read();
if(n==1){
puts("0");
return 0;
}
if(m==n){
for(int i=1;i<=n;i++)
printf("0 ");
return 0;
}
for(int i=1;i<=n;i++){
a[i]=(node){read(),i};
s+=a[i].val;
}
sort(a+1,a+n+1,cmp);
for(int i=1;i<=n;i++)
sum[i]=sum[i-1]+a[i].val;
k-=s;
for(int i=1;i<=m;i++){
int l=0,r=k,res=-1;
while(l<=r){
int mid=(l+r)>>1;
if(query1(i,mid))r=mid-1,res=mid;
else l=mid+1;
}
ans[a[i].pos]=res;
}
for(int i=m+1;i<=n;i++){
int l=0,r=k,res=-1;
while(l<=r){
int mid=(l+r)>>1;
if(query2(i,mid))r=mid-1,res=mid;
else l=mid+1;
}
ans[a[i].pos]=res;
}
for(int i=1;i<=n;i++)
printf("%lld ",ans[i]);
bool MED;
cerr<<(&MED-&MBE)/1048576.0<<" MB, "<<1000*clock()/CLOCKS_PER_SEC<<" ms\n";
return 0;
}