\(Prüfer\)序列可以适用于很多树上计数问题
转化(无根树到\(Prüfer\)序列):
给定一颗树,将树变成\(Prüfer\)序列,盗图!!!嘿嘿
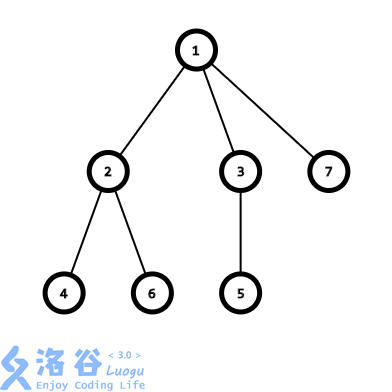
1.找到一个度数为\(1\)的点,且编号最小的点(编号最小保证了\(Prüfer\)序列的唯一对应性)
2.把这个点的父亲节点加入序列,然后把这个点删除
重复进行这两个操作,直至树中只剩下两个点,然后就得到了一个长度为\(n-2\)的序列,这就是\(Prüfer\)序列
模拟求\(Prüfer\)序列的过程:
- 找到\(4\)号节点,将\(fa[4]\)加入序列,然后将其删去。此时序列:\(\{2\}\)。
- 找到\(5\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{2,3\}\)。
- 找到\(3\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{2,3,1\}\)。
- 找到\(6\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{2,3,1,2\}\)。
- 找到\(2\)号节点,将其父结点加入序列,然后将其删去。此时序列:\(\{2,3,1,2,1\}\)。
所以,最后得到的\(Prüfer\)序列就是\(\{2,3,1,2,1\}\)。
转化(从\(Prüfer\)序列到无根树)
1.取出\(Prüfer\)序列最前面的元素\(x\)
2.取出在点集中,并且当前不在\(Prüfer\)序列中的最小元素\(y\),(对应着上面提到过的选取编号最小的点)
3.在\(x\),\(y\)中链接一条边
最后,在点集中剩下的两个点中连一条边
显然这有\(n-1\)条边,不会形成环,因此是一颗树
模拟过程
- 取出\(2,4\)连边。此时\(Prüfer\)序列:\(\{3,1,2,1\}\),\(V=\{1,2,3,5,6,7\}\)。
- 取出\(3,5\)连边。此时\(Prüfer\)序列:\(\{1,2,1\}\),\(V=\{1,2,3,6,7\}\)。
- 取出\(1,3\)连边。此时\(Prüfer\)序列:\(\{2,1\}\),\(V=\{1,2,6,7\}\)。
- 取出\(2,6\)连边。此时\(Prüfer\)序列:\(\{1\}\),\(V=\{1,2,7\}\)。
- 取出\(1,2\)连边。此时\(Prüfer\)序列:\(\{\}\),\(V=\{1,7\}\)。
最后在\(1,7\)间连边,就可以得到原树了。
性质,结论
-
基础性质:\(Prüfer\)序列与无根树一一对应,唯一对应性
-
度数为\(d_i\)的节点会在\(Prüfer\)序列中出现\(d_i-1\)次
-
一个\(n\)节点的完全图的生成树个数为\(n^{n-2}\)
对于一个\(n\)个节点的无根树,它的\(Prüfer\)序列长为\(n-2\),而每一个位置都有\(n\)种可能性,所以可能出现的\(Prüfer\)序列有\(n^{n-2}\)种 -
对于给定度数\(d_{1 \sim n}\)的一颗无根树共有\(\frac{(n-2)!}{\prod_{i=1}^n(d_i-1)!}\)种情况
由上面的性质可以知道,度数为\(d_i\)的节点会在\(Prüfer\) 序列中出现\(d_i-1\)次
则就是要求出\(d_i-1\)个\(i\)\((1\le i\le n)\)的全排列个数
而上面那个式子就是可重全排列公式。(即全排列个数除以重复元素内部的全排列个数)
[P6086 【模板】Prüfer 序列](P6086 【模板】Prüfer 序列 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
模板题,写两个转换
#include"bits/stdc++.h"
using namespace std;
const int N=5e6+15;
#define inl inline
#define regi register
#define PII pair<int,int>
#define int long long
inl int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
int n,m;
int d[N],fa[N],p[N];//in fa Prüfer
int w_prufer(void)
{
int ans=0;
for(int i=1;i<n;i++) fa[i]=read(),d[fa[i]]++;
for(int i=1,j=1;i<=n-2;i++,j++)
{
while(d[j]) j++;
p[i]=fa[j];
while(i<=n-2&&!--d[p[i]]&&p[i]<j) p[i+1]=fa[p[i]],i++;
}
for(int i=1;i<=n-2;i++) ans^=i*p[i];
return ans;
}
int w_fa(void)
{
int ans=0;
for(int i=1;i<=n-2;i++) p[i]=read(),d[p[i]]++;
p[n-1]=n;
for(int i=1,j=1;i<n;i++,j++)
{
while(d[j]) j++;
fa[j]=p[i];
while(i<n&&!--d[p[i]]&&p[i]<j) fa[p[i]]=p[i+1],i++;
}
for(int i=1;i<n;i++) ans^=i*fa[i];
return ans;
}
signed main(void)
{
n=read(),m=read();
int ans=m==1?w_prufer():w_fa();
printf("%lld",ans);
return 0;
}
P2290 [HNOI2004] 树的计数
根据$ Prüfer $序列,我们可以把问题转化成这样。
给定 \(n-2\) 个数,其中有 \(n\) 种,每种有 \(d_i-1\) 个,求排列组合方式。
很容易得出公式 \(\frac{(n-2)!}{∏_{i=1}^n \max(d_i−1,1)!}\) (取 max 是因为防止乘 0 )
注意特判和答案\(\le10^{17}\)
#include"bits/stdc++.h"
using namespace std;
#define inl inline
#define regi register
#define PII pair<int,int>
#define int __int128
const int P=100000000000000003,N=215;
inl int read(void)
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:f,ch=getchar();
while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
void write(int x)
{
if(x<0)
putchar('-'),x=-x;
if(x>9)
write(x/10);
putchar(x%10+'0');
return;
}
int fac[N];
int qpow(int a,int b){int res=1;while(b){if(b&1)res=(__int128)res*a%P;a=(__int128)a*a%P;b>>=1;}return res;}
void init(int n)
{
fac[1]=1;
for(int i=2;i<=n;i++) fac[i]=(__int128)fac[i-1]*i%P;
}
int fac_(int k)
{
int ans=1;for(int i=1;i<=k;i++) ans=(__int128)ans*i%P;return ans;
}
int d[N],ans=1;
signed main(void)
{
int n=read();
for(int i=1;i<=n;i++) d[i]=read();
int temp=0,maxn=0,minx=P;
for(int i=1;i<=n;i++) temp+=d[i],maxn=max(maxn,d[i]),minx=min(minx,d[i]);
if(n==1)
{
cout<<!d[1]<<endl;
return 0;
}
if(temp!=n+n-2||(n!=1&&minx==0))
{
puts("0");
return 0;
}
ans=fac_(n-2);
for(int i=1;i<=n;i++) ans=(__int128)ans*max(qpow(fac_(d[i]-1),P-2),(int)1)%P;
write(ans);
return 0;
}