标签：task const cs149 int float mask asst1

Assign 1

Program 1: Parallel Fractal Generation Using Threads (20 points)

任务要求

• 修改mandelbrotThread函数使其可以多线程并行描绘Mandelbrot

报告

多线程对比 for view 1

sequential耗时 661.509 ms

线程数	加速比
2	1.92
3	1.60
4	228.484
5	231.265
6	163.364
7	167.895
8	143.013

观察到现象：加速比和线程数没有线性关系，并且当线程数为奇数时，执行时间反而上升了

对每一个线程进行分析：

thread 0 has row 400 cost time: 301.785
thread 1 has row 400 cost time: 744.402
thread 2 has row 400 cost time: 410.087

可以直到，线程1分配到任务耗时最多，这是一个典型的负载不均衡的问题，因此我的做法就是把计算每一个点均匀shuffle到所有线程：

std::vector<int> stream(height * width);
std::iota(stream.begin(), stream.end(), 0);
std::random_device rd;
std::default_random_engine rng(rd());
std::shuffle(stream.begin(), stream.end(), rng);
int total = height * width;

for (int i=0; i<numThreads; i++) {

    // TODO FOR CS149 STUDENTS: You may or may not wish to modify
    // the per-thread arguments here.  The code below copies the
    // same arguments for each thread
    args[i].x0 = x0;
    args[i].y0 = y0;
    args[i].x1 = x1;
    args[i].y1 = y1;
    args[i].width = width;
    args[i].height = height;
    args[i].maxIterations = maxIterations;
    args[i].numThreads = numThreads;
    args[i].output = output;

    args[i].threadId = i;

    args[i].startRow = i * (height / numThreads);
    if(i == numThreads -1){
        args[i].numRows = height / numThreads + height %numThreads;
        args[i].stream.assign(stream.begin() + i* total / numThreads, stream.end());
    }else{
        args[i].numRows = height / numThreads;
        args[i].stream.assign(stream.begin() + i* total / numThreads, stream.begin() + (i+1)*total /numThreads);
    }

}
// serial
for(auto p:stream){
    int i = p / height;
    int j = p % height;
    float x = x0 + i * dx;
    float y = y0 + j * dy;

    int index = (j * width + i);
    output[index] = mandel(x, y, maxIterations);
}
     

最终加速比为5.32

使用16线程并没有明显区别，因为我的物理机只有4C8T

Program 2: Vectorizing Code Using SIMD Intrinsics (20 points)

任务描述

要求用simd指令将下面的函数重写：

void clampedExpSerial(float* values, int* exponents, float* output, int N) {
  for (int i=0; i<N; i++) {
    float x = values[i];
    int y = exponents[i];
    if (y == 0) {
      output[i] = 1.f;
    } else {
      float result = x;
      int count = y - 1;
      while (count > 0) {
        result *= x;
        count--;
      }
      if (result > 9.999999f) {
        result = 9.999999f;
      }
      output[i] = result;
    }
  }
}

报告

代码

这个题目还是很是比较简单的，把CS149intrin.h这个头文件中的函数大概看一下就能写出来了，我的代码：

void clampedExpVector(float* values, int* exponents, float* output, int N) {

  //
  // CS149 STUDENTS TODO: Implement your vectorized version of
  // clampedExpSerial() here.
  //
  // Your solution should work for any value of
  // N and VECTOR_WIDTH, not just when VECTOR_WIDTH divides N
  //
  __cs149_vec_float x;
  __cs149_mask mask;
  __cs149_mask all_mask = _cs149_init_ones();
  __cs149_vec_int exp;
  __cs149_vec_int const_zero = _cs149_vset_int(0);
  __cs149_vec_int const_one = _cs149_vset_int(1);
  __cs149_vec_float const_99 = _cs149_vset_float(9.999999f);
  __cs149_vec_float res;

  for(int i=0; i< (N - N % VECTOR_WIDTH); i+=VECTOR_WIDTH){
    mask = _cs149_init_ones(); // 这个如果都是0 那么代表结束游戏
    _cs149_vload_float(x, values+i, mask);
    _cs149_vset_float(res, 1.0f, mask);
    _cs149_vload_int(exp, exponents +i, mask);
    _cs149_vgt_int(mask, exp, const_zero, mask);
    _cs149_vlt_float(mask, x, const_99, mask);
    while(_cs149_cntbits(mask)!=0){
      _cs149_vmult_float(res, res, x, mask);
      _cs149_vsub_int(exp, exp, const_one, mask);
      _cs149_vgt_int(mask, exp, const_zero, mask);
      _cs149_vlt_float(mask, x, const_99, mask);
    }
    _cs149_vgt_float(mask, res, const_99, all_mask);
    _cs149_vmove_float(res, const_99, mask);
    _cs149_vstore_float(output+i, res, all_mask);
  }
  for(int i= (N- N % VECTOR_WIDTH); i < N; i++){ // 如果出现除不尽的情况有两种做法，padding和单独计算，这里简单点直接算
    float x = values[i];
    int y = exponents[i];
    if (y == 0) {
      output[i] = 1.f;
    } else {
      float result = x;
      int count = y - 1;
      while (count > 0) {
        result *= x;
        count--;
      }
      if (result > 9.999999f) {
        result = 9.999999f;
      }
      output[i] = result;
    }
  }
  
}

测试结果

不同vector width的影响

Vector Width	Vector Utilization
2	76.5%
4	68.3%
6	65.8%
8	64.2%
16	62.3%

现象：随着vector width不断增大，vector utilization的利用率不断下降

解释：因为我们的算法的终止条件是_cs149_cntbits(mask)!=0，只要有一个element的计算没有终止，算法就还得继续运行，所以相当于其他已经完成了的task在做无谓的等待。

Program 3: Parallel Fractal Generation Using ISPC (20 points)

任务描述

task1

编译学习ISPC，这里有一个大佬的笔记关于SPMD https://zhuanlan.zhihu.com/p/516448932

Intel的简单入门：https://ispc.github.io/example.html

Task 2

在data parallel的基础上，使用ispc的task parallel，创造多个task，每个task拥有一个gang。相当于多线程+simd两个优化一起加上

报告

Task1

编译运行代码

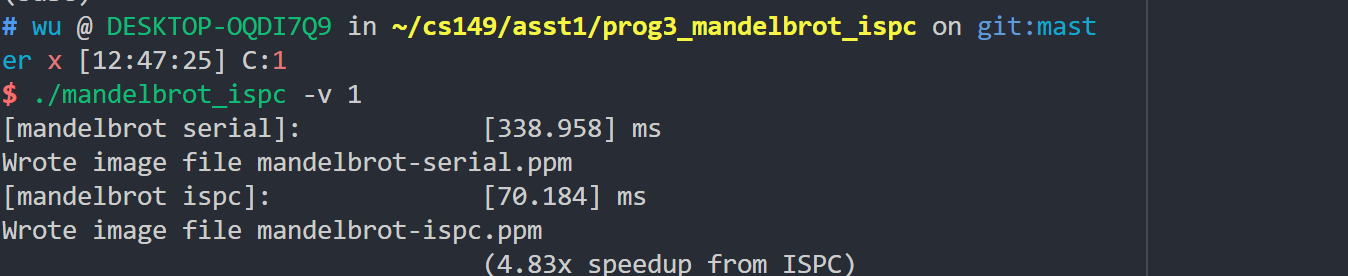
我的CPU是i7-1050u， 2C8T支持AVX2，也就是256bit，按道理可以加速比应该为8，但是实际上，加速比只是4.83

解释

在task parallel，也就是program 1中使用多线程来并行使，我们需要让线程负载均衡，也就是线程执行的代码耗时如果差不多效果最好。但是在data parallel中，也就是simd并行，事情反过来了。如果执行的复杂程度在数据集中分布均匀，那么在一个simd 8Byte计算，也就是8 lane中，有个lane计算很快，有的lane计算很慢，更加水桶效应，最终执行的时间就是最慢lane的执行时间。

在simd计算，我们应该让数据分布更加不均匀，计算简单的放在一块，计算复杂的数据放在一块，也就是gather。

Task2

编译运行代码

latc[2]： 创建两个task

可以看到加速比直接达到9.49

改变task数

改变ispc的latch，也就是task数，加速比也发生变化

Task数	加速比（倍）
2	9.49
4	12.33
8	17.23
16	28.80
32	30.60

我的i7 只有两个核有simd单元，如果task数超过了2，那么就是单纯是task级别的并行，没有data parallel级别的并行。

Program 4: Iterative sqrt (15 points)

任务描述

改变values的数据分布，使得最大化顺序执行速度，同时最小化ISPC的速度（这个不是教授发布的任务，但我觉得很有意思

报告

如果value全为1.0

算的最快，同样加速比也不高

如果value全为2.999，计算速度最慢，但是加速比很高

构造这样一个数据分布：

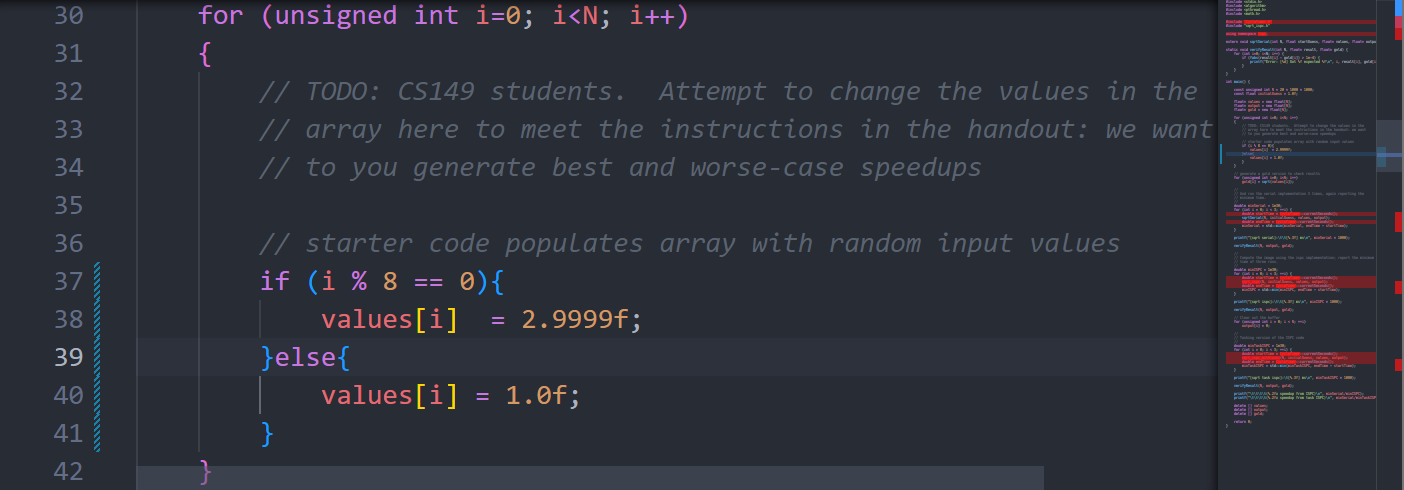
这样，simd中有一条lane算得很慢，严重拖累其他lane，最终的效果：

果然和我们预期一样，simd的加速甚至还不如serial直接算！

SIMD重写

用simd指令重写sqrt函数，一编译各种报错，发现我自己用了一大堆axv512 指令，我真的吐了，我在志强服务器上都没用上avx512，果然我还是太嫩了。。。simd，我劝你多学。

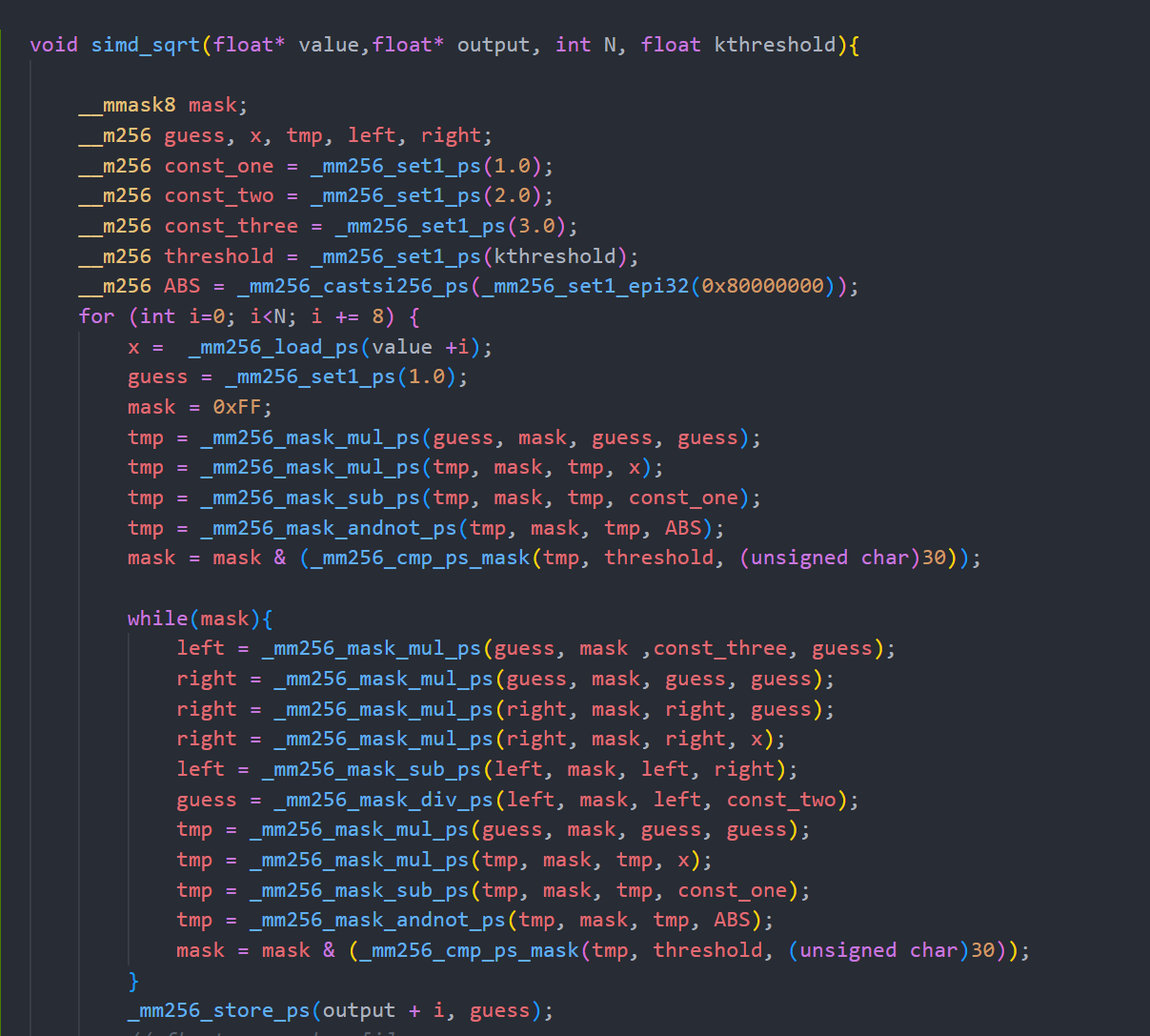
懒得改了，就这样吧。。摆了摆了

Program 5: BLAS saxpy

任务描述

使用ISPC来做向量乘法。

报告

task数设定为2

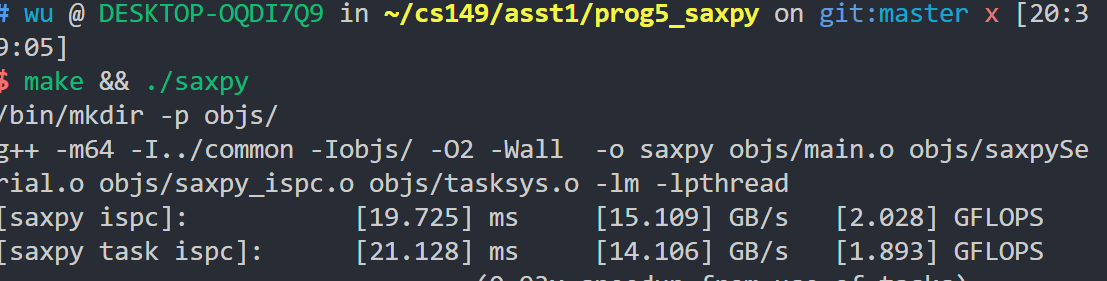
task数开到8

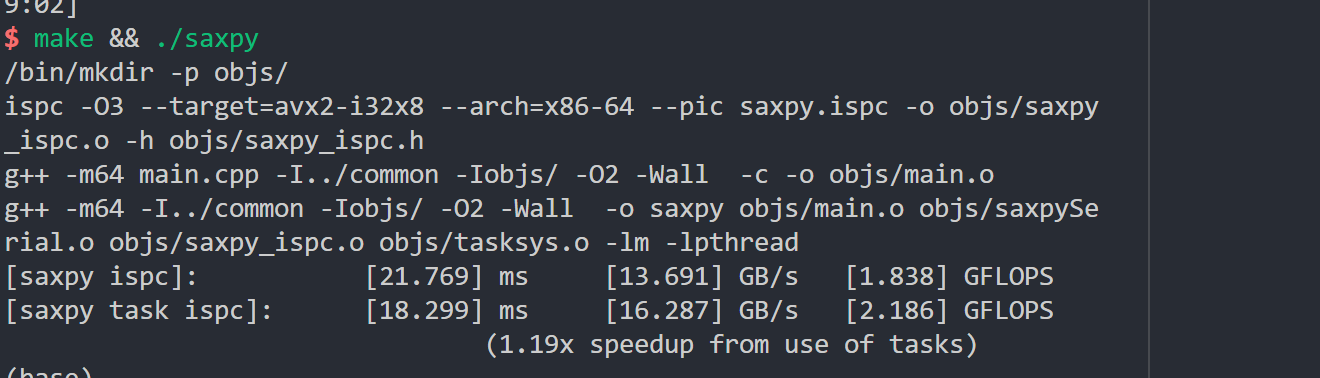
task数的增大对于对于提升很有限，看起来是因为不断读取内存和写内存，导致达到内存带宽。

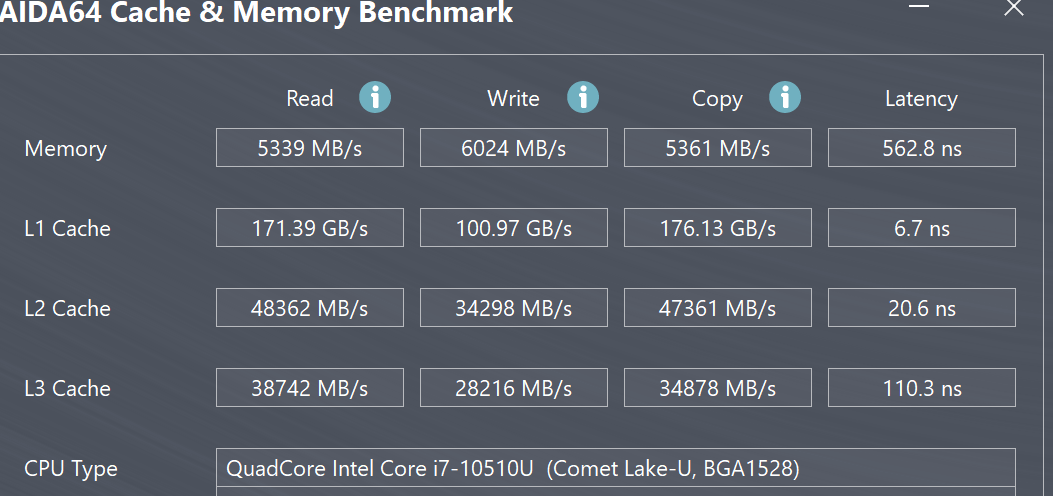
用aida64进行内存测试，发现内存读速度，只有5GB

进一步增大需要处理的数据，将需要处理数据的大小设置为1.6G，执行结果：

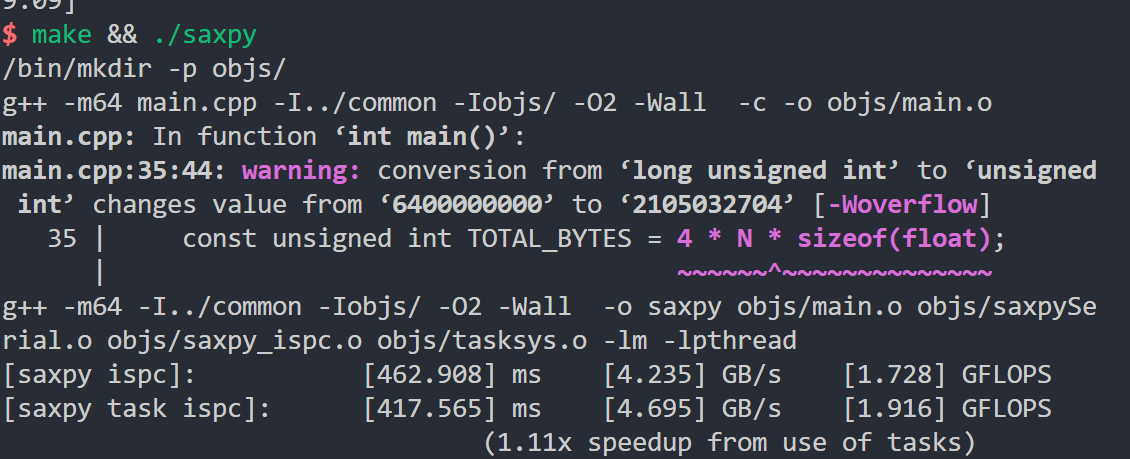
果然，这里内存带宽才是限制，计算已经不是限制了。

Program 6: Making K-Means Faster

摆烂了，摆烂了，这个日后空有再写

标签：task,const,cs149,int,float,mask,asst1
From： https://www.cnblogs.com/kalicener/p/16824312.html