KMP
KMP-字符串匹配算法,pat模式串,长度为M; txt文本串,长度为N。KMP算法是在txt中查找子串pat,如果存在,返回起始索引,否则返回-1 。
https://zhuanlan.zhihu.com/p/83334559这个知乎专栏讲得很好
根据上面的理解
1、如果是暴力枚举的话,就是在 txt枚举每一个字符,当这个字符与pat开头相同时,就继续枚举下去,直到不匹配,又从txt下一个字符开始匹配。这样太费时间,如:

当字符串中有很多重复的字符时,就会进行很多不必要的操作,比如pat中根本没有 c 这个字符,应该直接从txtc 后面的 a 开始匹配,但是暴力枚举只是单一的遍历txt的每一个字符。
2、我们想记录pat匹配的状态,记录当前pat匹配到哪一步了,这样就可以直接避免txt又回到前面重新遍历一次。
3、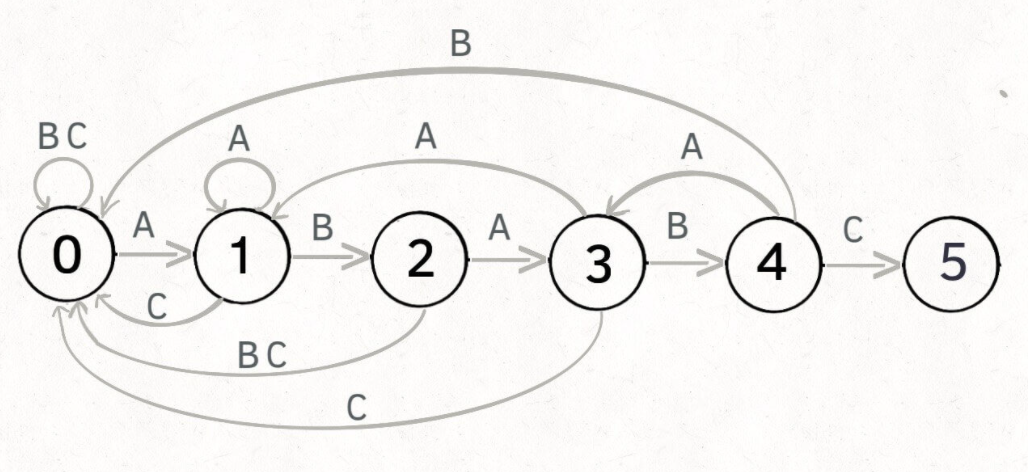
假设pat = ABABC,初始状态为0,箭头上的字母表示在当前状态下匹配到该字母的下一状态。这样就实现了一直遍历txt,然后判断pat当前的状态就行了。也就说pat的状态数组只与匹配串pat有关 。遇到不属于pat 的字符状态回到起始 0。
4、如何构建pat的状态数组
状态转移: 当前的匹配状态 和 遇到的字符
KMP实现算法
设模式串为 p,匹配串为s。
思考
next数组:如next[j]表示p[1~j]串中前缀和后缀相同的最大长度(部分匹配值)。
设p串: a b c a b
| p | a | b | c | a | b |
|---|---|---|---|---|---|
| 下标 | 1 | 2 | 3 | 4 | 5 |
| next[] | 0 | 0 | 0 | 1 | 2 |
next[5]:前缀 ab、 后缀 ab共同长度为2.
核心思想:在每次失配时,不是把p串往后移一位,而是把p串往后移动至下一次可以和前面部分匹配的位置,这样就可以跳过大多数的失配步骤。而每次p串移动的步数就是通过查找next[ ]数组确定的。
比如要在s = abababc寻找模式串p = ababc
- 前三个abc已经找到相同,但是第 5个
a != c-s[5] != p[4+1] - 这时候kmp 可以根据
next[]数组,因为next[4] = 2,说明前4个中组成的串前缀和后缀公共的部分有 2 个(ab ab),j = next[4] = 2,直接从第2 + 1个开始比较,前两个已经匹配过了,此时s[5] = a、p[2+1] = a,匹配到了aba,加上后面的bc,j到达了m,匹配完成。
匹配代码
匹配串s长度为n,模式串p为m
// 数据下标从1开始
for(int i = 1; j = 0; i <= n;i++) {
while(j && s[i] != p[j+1]) j = ne[j];
if(s[i] == p[j+1]) j++;
if(j == m) {
// 输出以0开始的匹配子串的首字母
cout << i - m; // 若从1开始则 +1
j = ne[j]; // 匹配多次就用这个
}
}
模式串next数组
构建next数组和匹配代码几乎一模一样,就是在模式串p找相同的前缀。
for(int i = 2, j = 0; i <= n;i++) {
while(j && p[i] != p[j+1]) j = ne[j];
if(p[i] == p[j+1]) j++; // 相同,之前的子串相同前缀后缀为j,相同统计直接+1
ne[i] = j; // 1-i中的相同前后缀长度为j
}
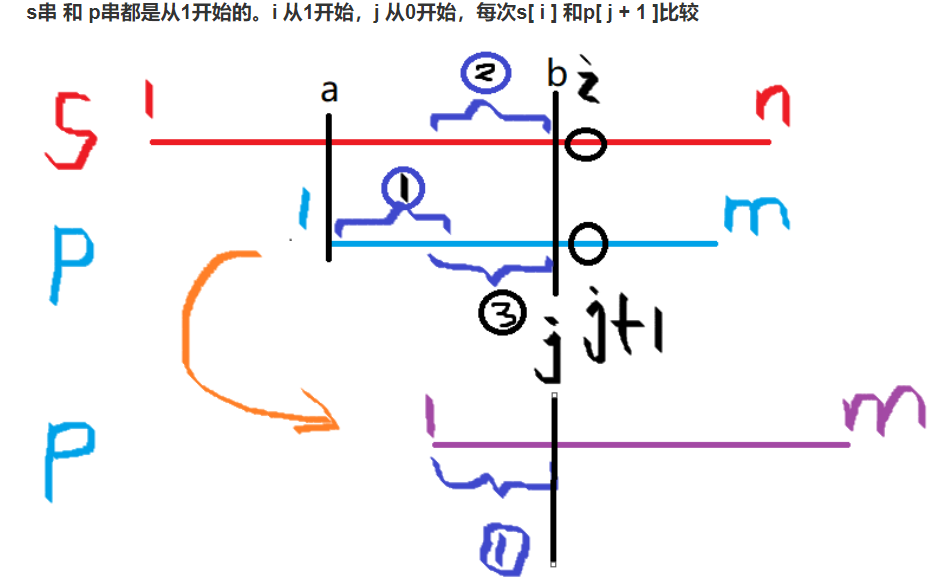
如上图。s[a,b] = p[1,j],但是当s[i]!=p[j+1]时,可以发现在匹配串p中1串等于3串,s中的2串和p中的3串相等也就是说我们可以直接从1串开始匹配,即j = next[j](前缀1和后缀3相同同的长度),然后从比较p[j+1] 和p[i]开始。这样就避免了s串的回头 。
ACwingKMP字符串
#include<iostream>
using namespace std;
const int N = 100010, M = 1000010;
int ne[N];
char p[N], s[M]; // p是模式串、s是匹配串
int main() {
int n,m;
cin >> n >> p+1 >> m >> s+1;
// 求next数组,模式串与自己匹配
for(int i = 2, j = 0;i <= n;i++) {
while(j && p[i] != p[j+1]) j = ne[j]; // 相当与从前缀(和后缀相同的位置)j
if(p[i] == p[j+1]) j++;
ne[i] = j;
}
// 利用next数组匹配需要匹配的串
for(int i = 1,j = 0; i <= m;i++) {
while(j && s[i] != p[j+1]) j = ne[j];
if(s[i] == p[j+1]) j++; // 相同的字符数量
if(j == n) {
cout << i - n << " "; // 本来是 i -n + 1,但我们初始时下标为1,本题是0
j = ne[j]; // 匹配下一个,从j位置开始,当前j相当于从ne[j]的位置再次匹配
}
}
return 0;
}