前言：

量是一定要积累的，但是不要一味的追求量，导致学完后面的知识，忘了前面的知识，得不偿失，那我们当然要避免这种情况，那就先花点时间复习昨天的内容。

........

........

过了10min

T9.添加小因子（e与phi不互素）

一.题目：

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(512)
q = getPrime(512)

e = 65537
while True:
    r = 2*getPrime(100)*e+1
    if isPrime(r):
        break

n = p*q*r

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'r = {r}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 7478755670255767435237487693415479182290330775502792675052667363676831056436638619069277770540533350723045234676443621124912287506103439704868369839725279
q = 9232828888049557325429111621080998490274442347556398052322580869768941301413255711626092627273543579067597113958627672298942570149816938335701615759283713
r = 102909133680612532601801231903654039
e = 65537
c = 142893174944324070830219394465469685943669308818639857030565389839224452373848570577201378981080333784852764502832587008270072323948511579823852437852643609820245476634896477031076952735298279618952398460203032125853063235638358942643559551563899381032067185778629120272032518475352761100115057449043142848203976076694124978394099839339406197
'''

关键步骤：

p = getPrime(512)
q = getPrime(512)

e = 65537
while True:
    r = 2*getPrime(100)*e+1
    if isPrime(r):
        break

n = p*q*r

这段代码是一个Python代码片段，它的主要目的是生成一个满足特定条件的素数r。下面是对这段代码的详细解释：

1. e = 65537：这行代码定义了一个变量e，并将其赋值为65537。65537是一个常用的公钥指数，在RSA加密算法中经常使用。
2. while True:：这是一个无限循环，意味着下面的代码块会不断执行，直到遇到break语句。
3. r = 2*getPrime(100)*e+1：这行代码计算r的值。首先，调用getPrime(100)函数（这个函数没有在代码片段中定义，但我们可以推测它的作用是返回一个大约100位的素数）。然后，将这个素数与e相乘，乘以2，最后加1。这个计算的目的是生成一个候选的r值，用于后续的素数检查。
4. if isPrime(r):：这行代码调用isPrime(r)函数（同样，这个函数没有在代码片段中定义，但可以推测它的作用是检查一个数是否是素数）来检查r是否是素数。
5. break：如果r是素数，break语句会被执行，从而退出while循环。

总的来说，这段代码的目的是找到一个满足特定条件的素数r，即r = 2*p*e+1，其中p是一个大约100位的素数，e是65537。这个r通常用于RSA加密算法中的公钥或私钥的一部分。

二.解题wp以及代码：

1.思路: 忽略小因子求逆元,则e就与phi互素

遇到求不出逆元d（原因是r的出现让e与欧拉函数phi不互素了），这种攻击，留意一下是不是小明文攻击

可能是6个因子，就看看哪几个满足等式

就用那几个求欧拉

小明文攻击，满足条件，忽略r，用pq求欧拉函数，解d解flag

2.条件

（1）e与欧拉函数不互素

（2）满足条件m modpq=m mod pqr

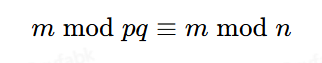
3.wp：

flag = b'NSSCTF{******}'

flag非常短，转换为数字非常小，满足条件

所以直接可以忽略r求欧拉函数

用pq求欧拉解出逆元d即可

4.工坊官方解

5.解题代码：

from Crypto.Util.number import *
from gmpy2 import *

p = 7478755670255767435237487693415479182290330775502792675052667363676831056436638619069277770540533350723045234676443621124912287506103439704868369839725279
q = 9232828888049557325429111621080998490274442347556398052322580869768941301413255711626092627273543579067597113958627672298942570149816938335701615759283713
r = 102909133680612532601801231903654039
e = 65537
c = 142893174944324070830219394465469685943669308818639857030565389839224452373848570577201378981080333784852764502832587008270072323948511579823852437852643609820245476634896477031076952735298279618952398460203032125853063235638358942643559551563899381032067185778629120272032518475352761100115057449043142848203976076694124978394099839339406197

n = p*q*r
phi = (p-1)*(q-1)
d = invert(e, phi)
m = pow(c, d, p*q)

print(long_to_bytes(m))

T10.e的倍数解m且（e与phi不互素)

一.题目：

from Crypto.Util.number import *

flag = b'NSSCTF{******}'

p = getPrime(512)
q = getPrime(512)

e = 65537*2

n = p*q

m = bytes_to_long(flag)

c = pow(m, e, n)

print(f'p = {p}')
print(f'q = {q}')
print(f'e = {e}')
print(f'c = {c}')

'''
p = 9927950299160071928293508814174740578824022211226572614475267385787727188317224760986347883270504573953862618573051241506246884352854313099453586586022059
q = 9606476151905841036013578452822151891782938033700390347379468858357928877640534612459734825681004415976431665670102068256547092636766287603818164456689343
e = 131074
c = 68145285629092005589126591120307889109483909395989426479108244531402455690717006058397784318664114589567149811644664654952286387794458474073250495807456996723468838094551501146672038892183058042546944692051403972876692350946611736455784779361761930869993818138259781995078436790236277196516800834433299672560
'''

关键步骤：

e = 65537*2

二.解题wp以及代码：

1.思路:将e的平方看做一个整体，求逆元解

将m的2次方看做m，解密即可

2.条件 m**2<n

注意条件（m**2<n）

因为大于n之后，m平方取模n就将m**2破坏了

(m**2>n的情况今天不学，后面学)

3.解题代码：

from Crypto.Util.number import *
from gmpy2 import *

p = 9927950299160071928293508814174740578824022211226572614475267385787727188317224760986347883270504573953862618573051241506246884352854313099453586586022059
q = 9606476151905841036013578452822151891782938033700390347379468858357928877640534612459734825681004415976431665670102068256547092636766287603818164456689343
e = 131074
c = 68145285629092005589126591120307889109483909395989426479108244531402455690717006058397784318664114589567149811644664654952286387794458474073250495807456996723468838094551501146672038892183058042546944692051403972876692350946611736455784779361761930869993818138259781995078436790236277196516800834433299672560

n = p*q
phi = (p-1)*(q-1)
d = invert(e // 2, phi)
m = pow(c, d, p*q)

print(long_to_bytes(isqrt(m)))

结语：

来到第三天，RSA基础题型已经学习完成了，但是这点东西做正规赛RSA签到题的能力都还不具备，今天的学习时间有点少，就这样吧! 希望你能坚持下去