My Blogs

[ARC175E] Three View Drawing

哎，构造。

首先考虑 \(m=n^2\) 怎么做：显然是最上面一层填满第一条主对角线，第二层填满第二条主对角线...（主对角线指可以循环的对角线）。

把 \(n\) 变成满足 \(n^2\geq m\) 的最小的 \(n\)。然后考虑删去 \(n^2-m\) 个。可以发现（谁能发现啊啊啊）在矩形的右下角删掉一个 L 型即可。如果 \(n^2-m\) 是偶数则右下角的 \((n,n,n)\) 保留即可。

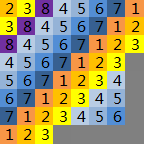
设 \(x\) 表示 \(L\) 的边长 \(-1\)（图中为 \(4\)）。上图是正方体的俯视图，把正方体从上到下分成 \(1,2,3\dots n\) 层，某个位置填了 \(x\) 代表这个的格子存在于第 \(x\) 层。

首先对于暖色调的填法，可以发现这样对于前 \(n-1-x\) 层，从正面和侧面看都是填满的，和俯视图是相同的。

对于紫色，这个位置填的是 \(n\)，正好对应了在第 \(n\) 层只有最左边三个有值，符合俯视图。

对于冷色调的其他颜色，都在一个 \((n-1)\times(n-1)\) 的正方形里面填的，所以对于第 \((n-x)\sim(n-1)\) 层，每层从正面和右面看都是恰好 \(n-1\) 个格子，也符合俯视图。

int n,m,a[510][510];
vector<tup> ans;
inline void mian()
{
	read(n,m),memset(a,-1,sizeof(a));
	while((n-1)*(n-1)>=m)--n;
	m=n*n-m;
	if(!(m&1))ans.eb(tup(n-1,n-1,n-1));else --m;
	m>>=1,assert(m<n);
	for(int i=0;i+m+1<n;++i)for(int j=0;j<n;++j)a[j][(i-1-j+n)%n]=i;
	for(int i=0;i<n-1-m;++i)a[i][n-2-m-i]=n-1;
	for(int i=n-m-1;i<n-1;++i)for(int j=0;j<n-1;++j)a[j][(i-j+(n-1))%(n-1)]=i;
	for(int i=0;i<n;++i)for(int j=0;j<n;++j)if(a[i][j]!=-1)ans.eb(tup(i,j,a[i][j]));
	for(auto [x,y,z]:ans)write(x,' ',y,' ',z,'\n');
}