简单版
题目描述
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\),求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
思路
我们可以将所有模式串存进 \(trie\) 树中,像这样:
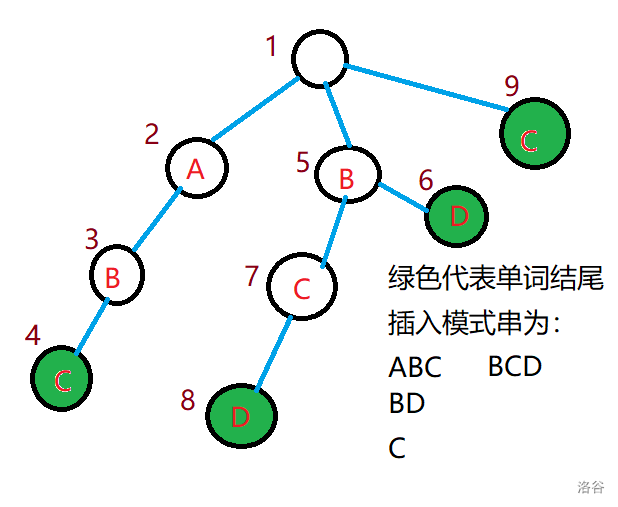
此时如果我们朴素地查找,那显然会超时,因此我们可以使用类似 \(KMP\) 算法的思想,对于每个点都创建一个 \(fail\) 指针,表示与当前节点表示的字符串在\(trie\) 树中出他自己外的后缀最长的那个所在位置,就拿图来举例吧,对于节点 \(4\) 他的表示的字符串为 \(ABC\),它的除它自己外的后缀有 \(C\),\(BC\),在 \(trie\) 中它们都存在,于是我们取最长的 \(BC\) ,它在 \(7\) 号节点,所以 \(fail_4=7\)。
那怎么求 \(fail\) 呢?这个我们可以用广搜来实现,毕竟一个点的 \(fail\) 显然不会比这个点深。那么一个点的 \(fail\) 就是它父亲的 \(fail\) 对应的当前节点的字符,也就是说若设 \(v\) 为当前节点,\(u\) 为它的父节点,\(i\) 为 \(v\) 这个节点存的字符,那么就有 \(fail[v]=nxt[fail[u]][i]\)。特别地,如果 \(v\) 还没建立我们可以让 \(v\) 直接等于它的 \(fail\) 值。
有了 \(fail\) 后,一切就好办了,只需要将要匹配的文本串在 \(trie\) 中查找,每到一个节点就不断跳 \(fail\) 更新答案,毕竟当前节点能匹配上,那它的后缀自然能匹配上嘛。
注意事项
一定不要重复记录一个点的贡献。
代码
#include<iostream>
#include<bitset>
#include<string>
#include<cstring>
#include<queue>
using namespace std;
namespace AC{
int nxt[1000010][26],cnt=0;
int end[1000010],fail[1000010];
queue<int>q;
void insert(string s){
int len=s.size();
int u=0;
for(int i=0;i<len;i++){
if(!nxt[u][s[i]-'a']){
nxt[u][s[i]-'a']=++cnt;
}
u=nxt[u][s[i]-'a'];
}
end[u]++;
return;
}
void build(){
queue<int>q;
for(int i=0;i<26;i++){
if(nxt[0][i]){
q.push(nxt[0][i]);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<26;i++){
if(nxt[u][i]){
fail[nxt[u][i]]=nxt[fail[u]][i];
q.push(nxt[u][i]);
}else{
nxt[u][i]=nxt[fail[u]][i];
}
}
}
return;
}
int query(string s){
int u=0,ans=0;
int len=s.size();
for(int i=0;i<len;i++){
u=nxt[u][s[i]-'a'];
for(int j=u;j&&end[j]!=-1;j=fail[j]){
ans+=end[j];
end[j]=-1;
}
}
return ans;
}
}
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
int n;
cin>>n;
for(int i=0;i<n;i++){
string t;
cin>>t;
AC::insert(t);
}
AC::build();
string s;
cin>>s;
cout<<AC::query(s)<<endl;
return 0;
}
加强版
题目描述
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\),求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
思路
这题跟前一题咋看区别并不大,很容易想到用数组记录答案,每匹配上一次就更新答案,但是这样做由于一个点会被访问不止一次,时间复杂度无法接受,因此需要优化。我们来分析一下,就拿前面那张图举例:

我们会发现当到达 \(4\) 时,我们会接着一连更新 \(4,7,9\),到 \(7\) 时又会更新一遍 \(7,9\)。很显然,问题就是出在这里,我们每个点不断被一次一次地更新,导致时间复杂度过大。因此,我们需要找到一种方法能够一次性统计一个点的答案。
我们可以把每个 \(fail\) 当作一条边建图,易证这是一个 \(DAG\),我们可以不用不断跳 \(fail\) 只需要标记当前点,再跑一遍拓扑排序,在拓扑排序的同时进行递推,这样每个点只会被更新一次,大大降低了复杂度。
代码
#include<iostream>
#include<queue>
#include<string>
#include<cstring>
using namespace std;
namespace AC{
int nxt[12800][26],tot=0;
int ind[12800],fail[12800],cnt[160];
queue<int>q;
void reset(){
tot=0;
memset(nxt,0,sizeof(nxt));
memset(ind,0,sizeof(ind));
memset(fail,0,sizeof(fail));
memset(cnt,0,sizeof(cnt));
return;
}
void insert(string s,int p){
int len=s.size();
int u=0;
for(int i=0;i<len;i++){
if(!nxt[u][s[i]-'a']){
nxt[u][s[i]-'a']=++tot;
}
u=nxt[u][s[i]-'a'];
}
ind[u]=p;
return;
}
void build(){
queue<int>q;
for(int i=0;i<26;i++){
if(nxt[0][i]){
q.push(nxt[0][i]);
}
}
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=0;i<26;i++){
if(nxt[u][i]){
fail[nxt[u][i]]=nxt[fail[u]][i];
q.push(nxt[u][i]);
}else{
nxt[u][i]=nxt[fail[u]][i];
}
}
}
return;
}
int query(string s){
int u=0;
int len=s.size();
for(int i=0;i<len;i++){
u=nxt[u][s[i]-'a'];
for(int j=u;j;j=fail[j]){
cnt[ind[j]]++;
}
}
int ans=0;
for(int i=1;i<=tot;i++){
if(ind[i]){
ans=max(ans,cnt[ind[i]]);
}
}
return ans;
}
}
string t[160];
int main(){
cin.tie(0);
ios::sync_with_stdio(false);
int n;
while(cin>>n&&n){
AC::reset();
for(int i=1;i<=n;i++){
cin>>t[i];
AC::insert(t[i],i);
}
AC::build();
string s;
cin>>s;
int ans=AC::query(s);
cout<<ans<<"\n";
for(int i=1;i<=n;i++){
if(AC::cnt[i]==ans){
cout<<t[i]<<"\n";
}
}
}
cout<<flush;
return 0;
}