DATE #:20240821
ITEM #:DOC
WEEK #:WEDNESDAY
DAIL #:捌月拾捌
``` 此情可待成追忆,只是当时已惘然 -- 《锦瑟》 李商隐 ```TAGS
<iframe border="0" frameborder="no" height="86" marginheight="0" marginwidth="0" src="//music.163.com/outchain/player?type=2&id=1406119516&auto=0&height=66" width="330"></iframe> < BGM = "琴师--要不要买菜" > < theme = oi-contest > < [NULL] > < [空] > < [空] >
T1 试卷答案(exam)
时间限制: 1 s 内存限制: 512 MB 测评类型: 传统型
题目背景
在考试前一天晚上,小 A 梦到了试卷的答案。
题目描述
试卷由若干道不定项选择题构成,只有 ABCD 四个选项。每道题的答案是一个按字典序排列的非空字符串。例如,A、CD 是合法的答案,而 BB、DC 不是合法的答案。
所有题的答案构成了一个字符串。
梦醒后,小 A 连忙记下了梦中的答案。现在他可能会对这个答案字符串进行一些修改,把一段区间内的选项变为下一个选项,并且他想知道对于一个子串,共有多少种不同的包含恰好 \(k\) 道题的试卷,其答案恰为这个子串。两份试卷不同当且仅当某道题号相同的不定项选择题的答案不同。
具体来说,小 A 给定了一个长度为 \(n\) 的由 ABCD 构成的字符串 \(S\),接下来要进行 \(q\) 次操作,分为以下两种:
\(1,l,r\):对于 \(l\le i \le r\),将 \(S_i\) 变为下一个选项,即 A 变为 B,B 变为 C,C 变为 D,D 变为 A。
\(2,l,r,k\):对于字符串 \(S\) 从 \(l\) 到 \(r\) 构成的子串,求有多少种不同的包含恰好 \(k\) 道题的试卷,其答案恰为这个子串。对于第二个操作,由于答案可能很大,你只需要求出答案对 \(998244353\) 取模的结果。
输入格式
第一行,两个整数 \(n,q\)。
第二行,长度为 \(n\) 的字符串 \(S\)。
接下来 \(q\) 行,每行第一个整数 \(op\),表示操作种类。
当 \(op=1\) 时,接下来包含两个整数 \(l,r\)。
当 \(op=2\) 时,接下来包含三个整数 \(l,r,k\)。
输出格式
对于第二个操作,输出一行一个整数,表示答案对 \(998244353\) 取模的结果。
输入输出样例
样例输入 #1
5 6 BACDA 2 1 4 2 1 2 3 2 1 5 4 1 2 3 2 1 5 4 2 1 5 5样例输出 #1
1 1 2 1样例 #2
见右侧「附件下载」中的
ex_exam2.in/out。样例 #3
见右侧「附件下载」中的
ex_exam3.in/out。数据范围与约定
对于 \(20\%\) 的数据,满足 \(1\le n,q \le 10^3\)。
对于另外\(30\%\) 的数据,满足 \(op=2\)。
对于 100%\(100\%\) 的数据,满足\(1\le n,q \le 10^5\),\(1\le op \le 2\),\(1\le l \le r \le n\),\(1\le k \le n\)。
//2024.8.21
//by white_ice
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 100005;
constexpr int mod = 998244353;
int n,q;char ch;
int st[oo];
__inline int add(int x){return x+1>=4?x+1-4:x+1;}
struct nod{itn laz,le,re,sim[4];}tree[oo<<2];
__inline bool pass(int id,itn p){return ((tree[id<<1].re+p)%4>=(tree[id<<1|1].le+p)%4);}
__inline void pushup(itn id){
tree[id].le=tree[id<<1].le;tree[id].re=tree[id<<1|1].re;
for(int i=0;i<=3;i++)
tree[id].sim[i]=tree[id<<1].sim[i]+tree[id<<1|1].sim[i]+pass(id,i);
}
__inline void addtag(int id,int p){
for (itn i=0;i<p;i++)
for (itn j=0;j<3;j++)
swap(tree[id].sim[j],tree[id].sim[j+1]);
(tree[id].laz+=p)%=4;
(tree[id].le+=p)%=4;
(tree[id].re+=p)%=4;
}
__inline void pushdown(int id){
if (tree[id].laz){
addtag(id<<1,tree[id].laz);
addtag(id<<1|1,tree[id].laz);
tree[id].laz = 0;
}
}
__inline void build(itn l,int r,itn id){
if (l==r){return tree[id].le=tree[id].re=st[l],void();}
int mid = (l+r)>>1;
build(l,mid,id<<1);
build(mid+1,r,id<<1|1);
pushup(id);
}
__inline void updata(itn l,int r,int nl,int nr,int id){
if (l>nr||r<nl)return void();
if (l>=nl&&r<=nr){return addtag(id,1);}
itn mid = (l+r)>>1;pushdown(id);
updata(l,mid,nl,nr,id<<1);
updata(mid+1,r,nl,nr,id<<1|1);
pushup(id);
}
int lre;
__inline int query(int l,int r,int nl,int nr,int id){
if (l>nr||r<nl)return 0;
if (l>=nl&&r<=nr){
int p = lre;lre = tree[id].re;
return tree[id].sim[0]+(p>=tree[id].le);
}
int mid = (l+r)>>1;
pushdown(id);int out = 0;
out += query(l,mid,nl,nr,id<<1);
out += query(mid+1,r,nl,nr,id<<1|1);
return out;
}
itn c[oo],ic[oo];
__inline int qpow(itn a,int b){itn res=1;while(b){
if(b&1)(res*=a)%=mod;b>>=1;(a*=a)%=mod;}return res;}
__inline int getc(itn a,int b){return c[a]*ic[b]%mod*ic[a-b]%mod;}
main(void){
//fre();
cin.tie(0)->sync_with_stdio(0);
cin >> n >> q;
c[0] = 1;
for (itn i=1;i<=n;i++)c[i] = c[i-1]*i%mod;
ic[n] = qpow(c[n],mod-2);
for (itn i=n;i>=1;i--)ic[i-1] = ic[i]*i%mod;
for (itn i=1;i<=n;i++){cin>>ch;st[i]=ch-'A';}
build(1,n,1);
while (q--){
itn op,l,r,k;
cin >> op >> l >> r;
if (op==1)
updata(1,n,l,r,1);
else {
cin >> k;k--;
lre = -1;
itn cnt = query(1,n,l,r,1);
//p_(cnt);
if (cnt>k) cout << 0 << '\n';
else cout << getc(r-l-cnt,k-cnt) << '\n';
}
}
exit(0);
}
使用线段树记录每个字符转化后的不下降子序列
开四棵树分别维护即可
我们在每次查询时,考虑是否需要将两面的线段合并
在线段树的每个节点上同时记录该区间的左端点和右端点字符
合并时进行比较
考虑是否需要将区间内序列数减一
在得出一段区间内上升序列数时
考虑该怎么计数,在求出序列数时,如果序列数大于k
那么一定不满足要求,当小于k时,我们要将这些段分开,多加入k-序列数个段,
也就是加入这么多断点
使用组合意义计数
设段中有序列数为x
那么数量就是\(C_{l-r-x}^{k-x}\),通过此计数即可
T2 [A+B Problem(ez)](#2310. A+B Problem(ez) - 题目 - 石家庄二中信息学在线评测系统 (sjzezoj.com))
时间限制: 2 s 内存限制: 512 MB 测评类型: 传统型
题目描述
A
本题有 \(T\) 组数据。对于一组数据,有 \(q\) 组询问,每次询问给定两个非负整数 \(a,b\),输出 \((a+b)\bmod2^{32}\)。你需要“离线”回答每组询问。具体地,记第 \(i\) 次回答的答案为 \(ans_i\),在第 \(i\) 组询问中你读入 \(a_i',b_i'\) 后,真正询问的值为 \(a_i=a_i' \oplus ans_{i−1},b_i=b_i' \oplus ans_{i−1}\)。特殊地,记 \(ans_0=ans_q\)。
请求出\(ans_1,...,ans_q\) 并输出。如果存在多组解,请输出字典序最小的解。
输入格式
本题有多组数据。第一行一个正整数 \(T\),表示测试数据组数。
对于每组数据,第一行一个正整数 \(q\)。 接下来 \(q\) 行,第 i 行两个非负整数 \(a_i' , b_i'\)。
数据保证 \(\sum q ≤ 3 × 10^5\),保证有解。
输出格式
对于一组数据,输出 \(q\) 行,第 \(i\) 行表示第 \(i\) 组询问的答案 \(ans_i\)。
输入输出样例
样例输入 #1
2 2 0 1 1 0 3 3 2 0 0 3 0样例输出 #1
1 1 1 2 3样例输入 #2
1 10 3749472293 4154891904 3224347513 4103595831 791851711 3055161978 4065152591 2368391812 3691608355 4160733936 3728210076 264996297 460392156 105250996 3455209177 2288371548 2800417316 1992099764 2564050154 2328370940样例输出 #2
853870281 3107817390 2771831525 2140636427 738673699 368934569 575141522 2581064217 782761450 1524864022数据范围与约定
\(1 ≤ T ≤ 2 × 10^4\)
\(1 ≤ q ≤ 3 × 10^5\)
\(0\le a_i,b_i\le 2^{32}-1\)
子任务 1(20分):\(q\le 32\)。
子任务 2(20分):\(q>32\)。
子任务 3(60分):无特殊限制。
//2024.8.21
//by white_ice
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn unsigned
#define int unsigned
constexpr int oo = 300005;
itn t;itn q;
int st[oo][2];
itn ned[oo];
main(void){
//fre();
// p_(1&1);
// p_(1&0);
// p_(0&0);
// p_(0&1);
cin.tie(0)->sync_with_stdio(0);
cin >> t;
while(t--){
cin >> q;
for(itn i=1;i<=q;i++){
cin >> st[i][0] >> st[i][1];
ned[i] = (st[i][1]&1)^(st[i][0]&1);
}
for(itn i=0;i<32;i++){
for(itn j=0;j<q;j++){
int p = (q+j-1)%q;
ned[j+1]|=((st[j+1][0]^ned[p+1])+
(st[j+1][1]^ned[p+1]))&(1<<i);
}
}
copy(ned+1,ned+q+1,ostream_iterator<unsigned>(cout,"\n"));
}
exit (0);
}
不会逐位确定的厉害做法。
测试若干组随机数据发现解存在且唯一。
考虑知道上一个答案之后递推当前答案,答案首先会异或 \(a_i+b_i\)。
然后考虑上一个答案的第 \(i\) 位为 1\(1\) 会对当前的答案产生什么影响。
容易发现如果当前的 \(a_i\) 和 \(b_i\) 在第 \(i\) 位不同,异或一下也等同于没有影响。
如果相同的话,设下一个满足 \(a_i\) 和 \(b_i\) 在当前位相同的位为第 \(j\) 位,那么答案的第 \(i+1\) 到 \(j\) 位全部异或了 \(1\),如下图。
换句话说,如果当前的 \(a_i\) 和 \(b_i\) 在第 \(i\) 位不同且按照上述方法确定了 \(j\),那么当前答案的第 \(i+1\) 到 \(j\) 位全部异或上一个答案的第 \(i\) 位。
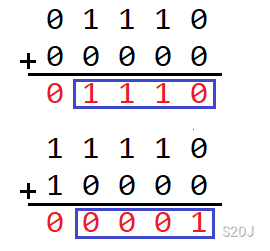
(作图失误,从左到右为二进制位从低到高)
设变量 \(x_0,x_1\dots x_{31}\) 为 \(ans_0\) 从左往右的每一位的值,则根据上面的分析,\(ans_i\) 的每一位的值都可以看做某个 \(x_i\) 和 \(0/1\) 异或起来。
可以直接递推后由 高斯消元。由于解存在且唯一,高斯消元是可以进行的。
看不懂题解可以看代码。
场上写+调这个玩意花了 2.5h 快吐血了,鉴定为诈骗。
T3 编队(team)
时间限制: 2 s 内存限制: 512 MB 测评类型: 传统型
题目描述
小 Z 喜欢打某款游戏,在游戏中他有 \(n\) 个英雄,每个英雄有一个武力值 \(w_i\),现在他要将自己的英雄分为两队,每队人数任意。
他发现如果两个英雄 \(i\) 与 \(j\) 的武力值相加不小于 \(m\) 且不在同一队,那么这两个英雄就可以打出组合技。
请问最多能有多少对英雄打出组合技(一个英雄可能打出多个组合技),同时还需算出有多少种分队方案可以达到此效果。
输入格式
第一行两个正整数 \(n, m\)。
第二行 \(n\) 个自然数,第 \(i\) 个表示 \(w_i\)。
输出格式
一行两个整数,用空格隔开,分别表示最多的配合默契对数与可以达到此效果的方案数,方案数对 \(10^9 + 7\) 取模。
输入输出样例
样例输入 #1
2 10 5 5样例输出 #1
1 2样例解释 #1
样例 1 的解释与说明。
样例 #2
见右侧「附件下载」中的
ex_data2.in/out。数据范围与约定
对于全部数据,\(n \leq 2000, m \leq 2×10^6, w_i \leq 10^6\)。
存在 30%\(30 \%\) 的数据满足 \(n \leq 18\)。
另有 20%\(20 \%\) 的数据满足 \(w_i\) 排序后是等差数列。
//2024.8.21
//by white_ice
//#2311. 编队(team)
//计数,DP
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 2003;
constexpr int inf = 0x3f3f3f3f;
constexpr int mod = 1000000007;
itn n,m;int sp[oo];
int rm[oo],stc[oo];
struct nod{itn v=-inf,c=0;
nod(int vl=-inf,int cl=0){v=vl,c=cl;}}f[oo][oo];
__inline nod operator+(nod a,int b){a.v = a.v+b;return a;}
__inline nod operator*(nod a,nod b){if(a.v>b.v)return a;
if(a.v<b.v)return b; (a.c+=b.c)%=mod;return a;}
itn pw[oo];
main(void){
//fre();
cin.tie(0)->sync_with_stdio(0);
cin >> n >> m ;
for (itn i=1;i<=n;i++)cin >> sp[i];
sort(sp+1,sp+n+1,greater<int>());
int tmp = n;
for(int i=1;i<=n;i++){
while(tmp>0&&sp[i]+sp[tmp]<m)tmp--;
rm[i]=min(i-1,tmp);
}
int k=1;
while(k<=n&&rm[k]==k-1)k++;
for(int i=k;i<=n;i++)stc[rm[i]]++;
f[0][0]=(nod){0,1}; pw[0]=1;
for(int i=1;i<=n;i++)
pw[i]=2*pw[i-1]%mod;
for(int i=1;i<k;i++){
for(int j=0;j<=i;j++){
f[i][j]=f[i-1][j]+j;
if(j)f[i][j]=f[i][j]*(f[i-1][j-1]+(i-j));
}
for(int j=0;j<=i;j++){
f[i][j]=f[i][j]+(stc[i]*max(j,i-j));
if(j+j==i)f[i][j].c=pw[stc[i]]*f[i][j].c%mod;
}
}
nod out;
for(int i=0;i<k;i++) out=out*f[k-1][i];
while(stc[0]--) out.c=2*out.c%mod;
cout << out.v << ' ' << out.c;
exit (0);
}
主要是转移顺序问题,我们希望的一个序列能满足对于某个位置,前面都满足一个条件,有了这个条件,前面的东西就可以一视同仁,只记录个数来处理。
很容易想到将数组排序后处理,发现这不行,因为可能转移的是之前的某个前缀,而此时当时的状态已经被破坏了。
考虑将某个数之前都放上能和他配对的,发现这是不现实的(手模一下根本做不到)
将限制放宽,将某个数之前都放上能和他配对的,或者都不能和他配对的。
再排好序的数组中,有这样的性质,若 \(a_1+a_n >=m\) 则 \(a_n\) 此时能和所有人配对。
反之 \(a_1\) 不能和所有人配对。
那我们分讨将其插到最后,就可以满足前面都能和他配对或都不能了。
另一种方法是考虑将 \(<m/2\) 的数,挂到最小的能和他配对的数上。
从大到小访问到挂到的这个点的时候,此时所有挂上的数只能和之前的大数配对,不能和之后的任何数配对,这也是满足转移条件的。
而 \(>m/2\) 的数能和所有大数配对,这也是满足的。
考虑挂上的小数应该如何放置,一定是贪心的放到当前最大的集合里面,如果一样大,那就是 \(2^cnt\) 次方。
注意有些小数谁都匹配不了,肯定是随便放就行。
这也是\(Retf\) 的做法。
一个类似的题: AT_arc148_e [ARC148E] ≥ K
T4 序列(seq)
时间限制: 1 s 内存限制: 512 MB 测评类型: 传统型
题目描述
有一个长度为 \(n\) 的序列 \(a_1,a_2,\dots,a_n\),序列里的每个元素都是 \([1,10^9]\) 内的正整数。
现在已知了 \(m\) 条信息,每条信息形如 \(i,j,k,x\),表示这个序列满足 \(a_i+a_j+a_k−\max(a_i,a_j,a_k)−\min(a_i,a_j,a_k)=x\)。
请构造一个满足条件的序列。
输入格式
第一行两个正整数 \(n,m\)。
接下来 \(m\) 行,每行四个正整数 \(i,j,k,x\),表示一条信息。
输出格式
如果无解,第一行输出
NO。如果有解,第一行输出
YES。第二行输出 \(n\) 个正整数 ,表示你构造的满足条件的序列 \(a\),你需要保证每个 \(a_i\) 都是 \([1,10^9]\) 内的正整数。输入输出样例
样例输入 #1
6 4 1 3 4 2 1 2 5 6 3 6 6 7 2 4 5 3样例输出 #1
YES 6 8 2 2 3 7样例输入 #2
5 4 1 2 3 4 2 3 4 5 3 4 5 3 1 3 4 6样例输出 #2
NO数据范围与约定
对于全部数据,\(1≤n,m≤10^5,1≤i,j,k≤n,1≤x≤10^9\)。
子任务 1(20 分):\(n,m≤10\)。
子任务 2(10 分):\(m=\binom n 3\),且对于任意一条信息,\(i≠j,j≠k,k≠i\),对于任意一个满足条件的集合 \(\{i,j,k\}\),在信息中恰好出现一条。
子任务 3(30 分):\(n,m≤1000\)。
子任务 4(40 分):无特殊限制。
//2024.8.21
//by white_ice
//#2312. 序列(seq)
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn int
constexpr int oo = 1e6+10;
int n,m;
int x[oo],y[oo],z[oo],val[oo];
vector <int>id[oo],d[oo];
int sta[oo],top;
bool vis[oo];
struct nod{int v,nxt;}ed[oo<<1];int head[oo],sum;
void add (int u,int v) {
ed[++sum].v = v;
ed[sum].nxt = head[u];
head[u] = sum;
}
int cnt,tot,belong[oo],dfn[oo],low[oo],dfntot;
void tarjan (int x) {
dfn[x] = low[x] = ++dfntot;
sta[++top] = x,vis[x] = 1;
for (int i=head[x];i;i=ed[i].nxt){
int to = ed[i].v;
if (!dfn[to]){
tarjan(to);
low[x] = min(low[x],low[to]);
}
else if(vis[to]) low[x] = min(low[x],dfn[to]);
}
if (low[x]==dfn[x]) {
++tot;
while (sta[top]!=x) {
vis[sta[top]]=0;
belong[sta[top]]=tot;
top--;
}
vis[sta[top]] = 0;
belong[sta[top]] = tot;
top--;
}
}
main(void){
//fre();
cin.tie(0)->sync_with_stdio(0);
cin >> n >> m;
for (int i=1;i<=m;i++) {
cin >> x[i] >> y[i] >> z[i] >> val[i];
d[x[i]].push_back(val[i]);
d[y[i]].push_back(val[i]);
d[z[i]].push_back(val[i]);
}
for (int i=1;i<=n;i++){
if (d[i].empty()) continue;
sort (d[i].begin(),d[i].end());
d[i].erase (unique(d[i].begin(),d[i].end()),d[i].end());
for (int j=0;j<int(d[i].size());j++) {
id[i].push_back(++cnt);
cnt++;
if (j) add(id[i][j],id[i][j-1]),
add(id[i][j-1]+1,id[i][j]+1);
}
}
for (int i=1;i<=m;i++) {
int a = lower_bound(d[x[i]].begin(),d[x[i]].end(),val[i])-d[x[i]].begin();
int b = lower_bound(d[y[i]].begin(),d[y[i]].end(),val[i])-d[y[i]].begin();
int c = lower_bound(d[z[i]].begin(),d[z[i]].end(),val[i])-d[z[i]].begin();
add(id[x[i]][a],id[y[i]][b]+1);
add(id[x[i]][a],id[z[i]][c]+1);
add(id[y[i]][b],id[x[i]][a]+1);
add(id[y[i]][b],id[z[i]][c]+1);
add(id[z[i]][c],id[x[i]][a]+1);
add(id[z[i]][c],id[y[i]][b]+1);
if (a && b) add(id[x[i]][a-1]+1,id[y[i]][b-1]),
add(id[y[i]][b-1]+1,id[x[i]][a-1]);
if (a && c) add(id[x[i]][a-1]+1,id[z[i]][c-1]),
add(id[z[i]][c-1]+1,id[x[i]][a-1]);
if (b && c) add(id[y[i]][b-1]+1,id[z[i]][c-1]),
add(id[z[i]][c-1]+1,id[y[i]][b-1]);
}
for (int i = 1; i <= cnt; i++)
if (!dfn[i]) tarjan(i);
for (int i = 1; i <= cnt; i++) {
for (int j = 0; j < int (d[i].size()); j++)
if (belong[id[i][j]] == belong[id[i][j]+1]) {
cout << "NO";
return 0;
}
}
cout << "YES\n";
for (int i = 1; i <= n; i++) {
if (d[i].empty()) {
cout << "1 ";
continue;
}
int x = 0;
for ( ; x < int (d[i].size()) && belong[id[i][x]] < belong[id[i][x]+1]; x++) ;
if (x == int (d[i].size()))
++d[i][--x];
cout << d[i][x] << ' ';
}
return 0;
}
这个条件还是比较好转化的:
就是 \(i,j,k\) 的中位数是 \(x\)。
三元限制不好处理,基本没有能处理三元限制的手段。
改成分讨+二元限制:
- 若 \(a_i>x\) ,则要求 \(a_j \le x \wedge a_k \le x\)
- 若 \(a_i<x\) ,则要求 \(a_j \ge x \wedge a_k \ge x\)
轮换一下,这样有 \(6\) 个条件。
发现都是 "若则" 类型的,想到了 sat。
发现都是且的关系,很好,不用拆了。
对于不等关系,我们设 \(p(i,x)\) 表示 \(i>x\) 成立,\(\neg p(i,x)\) 表示 \(i \le x\)
考虑满足这些约束是否考虑周全。
发现有些隐含的关系还没处理,一个类似前缀和差分大于 0 的问题:
显然有 \(p(i,x) \rightarrow p(i,x-k)\),\(\neg p(i,x) \rightarrow \neg p(i,x+k)\)
同时有 $p(i,0) = 1 \(,\)p(i,Inf) = 0$
这个强制等于的处理是如果不等于就推出等于,这样一定只能取等于。
当然每个点拆成值域个点是不可能的,我们只把和他有关的值存起来离散化。
最后求答案的时候需要注意,对于某个点拆成的一条链,他肯定是前一段满足 \(p(i,x)\) 后一段满足 \(\neg p(i,x)\),找到中间的分界点就是答案。
标签:oo,itn,le,21,10,2024.8,样例,int From: https://www.cnblogs.com/white-ice/p/18372630