前言
本题解部分思路来自于网络,仅供参考。
A - Shout Everyday
题目大意
给定 Takahashi 每天的睡觉时间和起床时间,求 Takahashi 在 $A$ 时是睡着的还是清醒的。
解题思路
根据题意模拟即可。
code
#include <bits/stdc++.h>
using namespace std;
int main() {
int a,b,c;
cin >> a >> b >> c;
if(b >= c) { //如果睡到了第二天
c += 24;
}
if((b <= a && a <= c) | (b <= a + 24 && a + 24 <= c)) {
printf("No\n");
} else {
printf("Yes\n");
}
return 0;
}
B - Cut .0
题目大意
给定一个有三位小数的浮点数,输出这个浮点数去除多余的 $0$ 和小数点后的数。
解题思路
直接输入这个数再输出即可。
code
#include <bits/stdc++.h>
using namespace std;
int main() {
double x;
scanf("%lf", &x);
printf("%g\n", x);
return 0;
}
C - Enumerate Sequences
题目大意
给定一个序列 $R$ ,按字典序所有长度为 $K$ 的,满足以下两个条件的数列:
- 数列的第 $i$ 个元素在 $[1,R_i]$ 之间。
- 数列和是 $K$ 的倍数。
解题思路
直接用dfs枚举即可。
code
#include <bits/stdc++.h>
using namespace std;
int r[15];
int ans[15];
int n, k;
void print() {
for (int i = 1; i <= n; i++) {
printf("%d ", ans[i]);
}
puts("");
}
void dfs(int ind, int sum) {
if (ind == n + 1) {
if (sum % k == 0) {
print();
}
return;
}
for (int i = 1; i <= r[ind]; i++) {
ans[ind] = i;
dfs(ind + 1, sum + i);
}
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) {
scanf("%d", r + i);
}
dfs(1, 0);
return 0;
}
D - Pedometer
题目大意
给出湖边 $N$ 个休息区中从一个休息区顺时针走到下一个休息区需要走的部署,求满足休息区 $s$ 顺时针走到休息区 $t$ 需要走的步数为 $M$ 的倍数,$(s,t)$ 对的个数。
解题思路
因为湖边 $N$ 个休息区在一个环上,考虑把输入的数组复制一遍,即把 $[2,1,4,3]$ 变成 $[2,1,4,3,2,1,4,3]$ 。
为了快速求出两个休息区之间的距离,我们对复制过后的数组做前缀和,复制过后的数组前缀和过后得到数组 $s$ 。
为了快速得出哪些区间的区间和是 $M$ 的倍数,我们进行分析。如果区间 $[i,j]$ 的区间和是 $M$ 的倍数,即 $s_j - s_{i - 1}\bmod M=0$ ,则:
$$ \because s_j - s_{i - 1} \bmod M = 0 \\ \therefore s_j - s_{i - 1} \equiv 0 \pmod{M} \\ \therefore s_j \equiv s_{i - 1} \pmod{M} $$所以,当 $s_j \equiv s_{i - 1} \pmod{M}$ 时,区间 $[i,j]$ 的区间和为 $M$ 的倍数。为了得出与 $s_i$ 同模的数,我们维护一个 $map$ ,$map[i]$ 表示有多少个 $s_j$ 满足 $s_j \bmod M = i$ 。每处理一个 $s_i$ ,答案就增加 $map[s_i \bmod M]$ ,并把 $s_i$ 加入 $map$ ,弹出 $s_{i - N + 1}$ 。
code
#include <bits/stdc++.h>
using namespace std;
int a[400005];
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
a[i + n] = a[i];
}
for (int i = 1; i <= 2 * n; i++) {
a[i] += a[i - 1];
a[i] %= m;
}
unordered_map<int, int> cnt;
long long res = 0;
for (int i = 2; i <= n; i++) cnt[a[i]]++;
for (int i = n + 1; i <= 2 * n; i++) {
res += cnt[a[i]];
cnt[a[i]]++;
cnt[a[i - n + 1]]--;
}
printf("%lld\n", res);
return 0;
}
[E - Permute K times](E - Permute K times (atcoder.jp))
题目大意
给定两个数组 $A$ 和 $X$ 和一个整数 $K$ ,求 $A$ 在进行了 $K$ 次操作
$$ A_i = A_{X_i} $$以后变成了什么。
解题思路
这道题可以看作一道图论题。
$A$ 数组的每一位可以看作图的节点,$K$ 数组的每一位可以看作图的边。
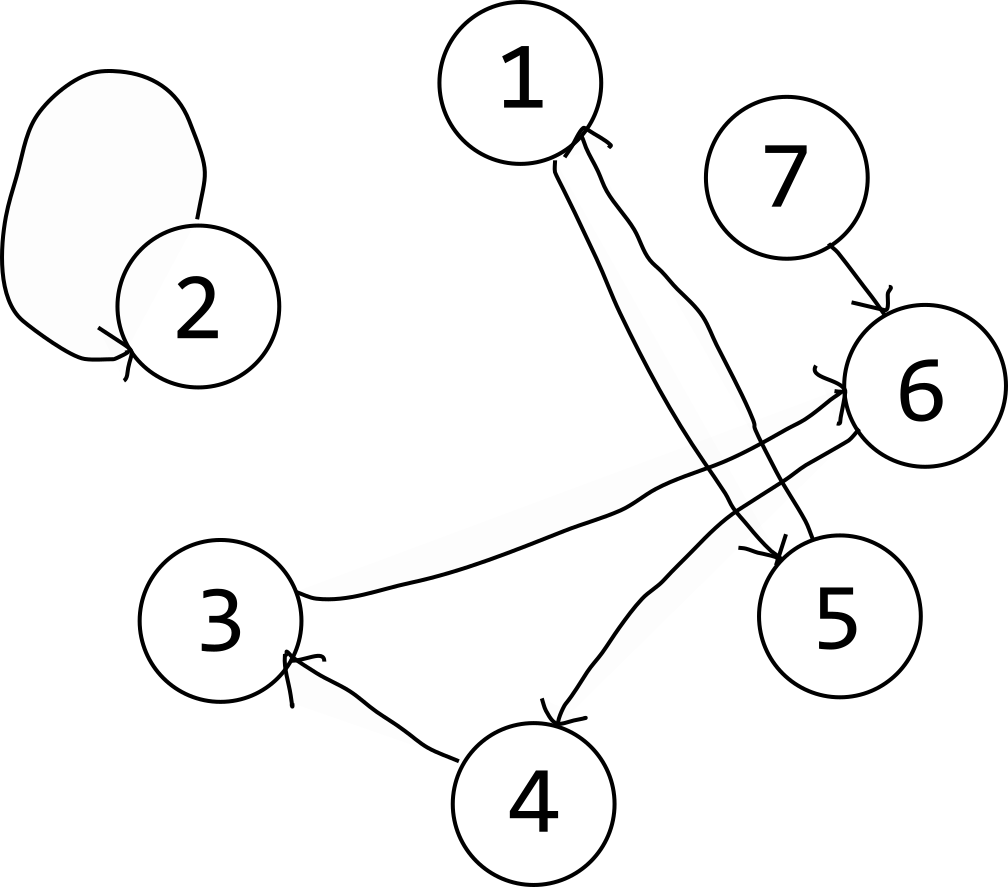
而每一次操作都可以看作是点在图上的运动。
为了快速求出每一个点在运动了 $K$ 步后到了哪里,我们维护一个倍增数组 $x[i][j]$ 表示第 $i$ 个点走了 $2^j$ 步后到了哪里。之后用倍增数组求出每一个点在进行了 $K$ 次操作之后到了哪里,最后输出结果。
code
#include <bits/stdc++.h>
using namespace std;
int a[200005];
int x[200005][64];
int main() {
int n;
long long k;
scanf("%d%lld", &n, &k);
for (int i = 1, t; i <= n; i++) {
scanf("%d", &t);
x[i][0] = t;
}
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
}
for (int i = 1; i <= 60; i++) {
for (int j = 1; j <= n; j++) {
x[j][i] = x[x[j][i - 1]][i - 1];
}
}
for (int i = 1; i <= n; i++) {
int p = i;
for (int j = 60; j >= 0; j--) {
if (k >> j & 1) p = x[p][j];
}
printf("%d ", a[p]);
}
puts("");
return 0;
}
F - Rearrange Query
题目大意
给定两个数组 $A$ 和 $B$ ,对于每一次询问 $l_i,\ r_i,\ L_i,\ R_i$ ,回答可不可以通过排列 $A[l_i...r_i]$ 使得 $A[l_i...r_i] = B[L_i...R_i]$ 。
解题思路
这道题直接使用哈希+前缀和即可。
code
#include <bits/stdc++.h>
#define MOD 156876589475701
#define MAX_N 200005
using namespace std;
int a[MAX_N], h[MAX_N], b[MAX_N], ph1[MAX_N], ph2[MAX_N];
int main() {
int n, q;
scanf("%d%d", &n, &q);
mt19937_64 mt(time(0));
for (int i = 1; i <= n; i++) {
h[i] = mt();
}
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
ph1[i] = (h[a[i]] + ph1[i - 1]) % MOD;
}
for (int i = 1; i <= n; i++) {
scanf("%d", b + i);
ph2[i] = (h[b[i]] + ph2[i - 1]) % MOD;
}
int l, r, L, R;
while (q--) {
scanf("%d%d%d%d", &l, &r, &L, &R);
if (ph1[r] - ph1[l - 1] == ph2[R] - ph2[L - 1]) {
puts("Yes");
} else {
puts("No");
}
}
return 0;
}