T1放了个啥?
T1读假了好几遍
首先一行不能为空,一列的空位必须相邻,一列可以为空
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N =2e2+5,mod=998244353;
int n,m;ll g[N][N],jie[N],inv[N];
ll qpow(ll a, ll b)
{
ll ans=1;
while(b)
{
if(b&1)ans=ans*a%mod;
b>>=1;a=a*a%mod;
}
return ans;
}
ll C(int n,int m)
{
return jie[n]*inv[m]%mod*inv[n-m]%mod;
}
int vis[N];ll ans=0;
ll calc(ll i)
{
return i*(i+1)/2;
}
map <ull,bool> mp;
void dfs(int u)
{
// cout<<u<<endl;
if(u==n+1)
{
int cnt=0;
for(int i=1;i<=m;i++){
cnt=0;int zero=0;
for(int j=1;j<=n;j++)
{
if(g[j][i])cnt++;
else
{
if(zero&&zero!=j-1)
{
return;
}
zero=j;
}
}
if(cnt==n)return ;
}
ull zt=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
zt=zt*10+(g[i][j]);
// cout<<g[i][j]<<" ";
}
// cout<<endl;
}
// cout<<endl;
ans++;
// if(!mp[zt])ans++;
// mp[zt]=1;
// cout<<zt<<endl;
return ;
}
for(int len=1;len<=m;len++)
for(int i=1;i+len-1<=m;i++)
{
for(int k=i;k<=i+len-1;k++)g[u][k]=1;
dfs(u+1);
for(int k=i;k<=i+len-1;k++)g[u][k]=0;
}
return;
}
int main()
{
speed();
freopen("magic.in","r",stdin);
freopen("magic.out","w",stdout);
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
cin>>n>>m;dfs(1);
// cout<<dfs(1)<<endl;
cout<<ans<<endl;
return 0;
}
暴力大赛
T2暴力,大道至简
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N = 2e5+5;
int n,m,be[N];vector <pii> edge[N];
inline int read()
{
int x=0,f=1;char ch=getchar_unlocked();
for(;ch<'0'||ch>'9';ch=getchar_unlocked())if(ch=='-')f=-f;
for(;ch>='0'&&ch<='9';ch=getchar_unlocked())x=(x<<3)+(x<<1)+(ch^48);
return x*f;
}
inline void write(int x)
{
x==0?void(0):(write(x/10),putchar_unlocked((x%10)|48),void(0));
}
int ans=0,dis[N];
inline void dfs(int u,int fa)
{
dis[u]=dis[fa]+1;
ans=max(ans,dis[u]);
for(auto [to,id]:edge[u])
{
if(to==fa||be[id])continue;
dfs(to,u);
}
}
int main()
{
speed();
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
freopen("block.in","r",stdin);
freopen("block.out","w",stdout);
// freopen("block1.in","r",stdin);
// freopen("out.out","w",stdout);
n=read();m=read();
int u,v;
for(int i=1;i<=n-1;i++)
{
u=read();v=read();
edge[u].pb({v,i});edge[v].pb({u,i});
}
int op;
for(int i=1;i<=m;i++)
{
op=read();
if(op==1)
{
u=read();
be[u]=1;
}
else if(op==2)
{
u=read();ans=0;
dis[0]=-1;
dfs(u,0);
ans==0?(putchar_unlocked('0'),void(0)):write(ans);
putchar_unlocked('\n');
}
}
return 0;
}
T3暴力\(dp\)
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N = 3e3+5;
int n,m,c,k,q,sum[N][N],dp[N][N],mu[N],diff[N][N];
struct jz
{
int x1,y1,x2,y2;
}a[N];
int lowbit(int x){return x&-x;}
void add(int x,int y,int v)
{
for(int i=x;i;i-=lowbit(i))
{
for(int j=y;j;j-=lowbit(j))
{
sum[i][j]+=v;
}
}
}
int query(int x,int y)
{
int ans=0;
for(int i=x;i<=n;i+=lowbit(i))
{
for(int j=y;j<=n;j+=lowbit(j))
{
ans+=sum[i][j];
}
}
return ans;
}
ll solve(int x,int y)
{
for(int i=0;i<=n;i++)
for(int j=0;j<=x;j++)dp[i][j]=0;
// memset(dp,0,sizeof dp);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=min(i,x);j++)
{
dp[i][j]=dp[i-1][j];
ll val=0;
for(ll k=1;k<=min(mu[i],m-mu[i])&&k<=y;k++)
{
val=max(val,(y-k)*k);
}
// cout<<val<<endl;
dp[i][j]=max<ll>(dp[i][j],dp[i-1][j-1]+val);
}
}
return dp[n][x];
}
void update(int x1,int y1,int x2,int y2)
{
diff[x1][y1]++;
diff[x2+1][y1]--;
diff[x1][y2+1]--;
diff[x2+1][y2+1]++;
}
int main()
{
speed();
freopen("army.in","r",stdin);
freopen("army.out","w",stdout);
// freopen("army1.in","r",stdin);
// freopen("in.in","r",stdin);
// freopen("out1.out","w",stdout);
cin>>n>>m>>c>>k>>q;
for(int i=1;i<=c;i++)
{
cin>>a[i].x1>>a[i].y1>>a[i].x2>>a[i].y2;
update(a[i].x1,a[i].y1,a[i].x2,a[i].y2);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+diff[i][j];
if(sum[i][j]>=k)mu[i]++;
// if(sum[i][j]>=k)mu[i]++;
// cout<<sum[i][j]<<" ";
}
// cout<<endl;
}
int x,y;
for(int i=1;i<=q;i++)
{
cin>>x>>y;
cout<<solve(x,y)<<endl;
}
return 0;
}
除了差分,还可以预处理出来,这样就不用\(dp\)了,至多\(40\)
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N = 3e3+5;
int n,m,c,k,q,sum[N][N],dp[N][N],mu[N],diff[N][N];
struct jz
{
int x1,y1,x2,y2;
}a[300005];
int lowbit(int x){return x&-x;}
void add(int x,int y,int v)
{
for(int i=x;i;i-=lowbit(i))
{
for(int j=y;j;j-=lowbit(j))
{
sum[i][j]+=v;
}
}
}
int query(int x,int y)
{
int ans=0;
for(int i=x;i<=n;i+=lowbit(i))
{
for(int j=y;j<=n;j+=lowbit(j))
{
ans+=sum[i][j];
}
}
return ans;
}
ll p[N][N],h[N][N];
ll solve(int x,int y)
{
return h[y][n]-h[y][n-x];
}
void update(int x1,int y1,int x2,int y2)
{
diff[x1][y1]++;
diff[x2+1][y1]--;
diff[x1][y2+1]--;
diff[x2+1][y2+1]++;
}
int main()
{
speed();
freopen("army.in","r",stdin);
freopen("army.out","w",stdout);
// freopen("army1.in","r",stdin);
// freopen("in.in","r",stdin);
// freopen("out1.out","w",stdout);
cin>>n>>m>>c>>k>>q;
for(int i=1;i<=c;i++)
{
cin>>a[i].x1>>a[i].y1>>a[i].x2>>a[i].y2;
update(a[i].x1,a[i].y1,a[i].x2,a[i].y2);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+diff[i][j];
if(sum[i][j]>=k)mu[i]++;
// if(sum[i][j]>=k)mu[i]++;
// cout<<sum[i][j]<<" ";
}
// cout<<endl;
}
for(int y=1;y<=m;y++)
{
for(int i=1;i<=n;i++)
{
ll b=min(mu[i],m-mu[i]);
p[y][i]=min<ll>(b,y/2)*(y-min<ll>(b,y/2));
}
sort(p[y]+1,p[y]+1+n);
for(int i=1;i<=n;i++)
h[y][i]=h[y][i-1]+p[y][i];
}
int x,y;
for(int i=1;i<=q;i++)
{
cin>>x>>y;
cout<<solve(x,y)<<endl;
}
return 0;
}
T4暴力\(dp\)
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N = 2e6+5,mod=998244353;;
int n,q;
int st=1,ed;
int g[N][25];ll dp[N][25];
int len=0;
char s[N];
int xx[5]={0,1,2,1,2};
int yy[5]={0,2,1,-2,-1};
inline int solve(int ta,int tb)
{
for(int i=st;i<=ed;i++)
for(int j=1;j<=n;j++)
dp[i][j]=0;
dp[st][ta]=1;
// cout<<st<<" "<<ed<<" "<<n<<endl;
for(int i=st;i<=ed;i++)
{
for(int j=1;j<=n;j++)
{
if(dp[i][j]&&g[i][j])
{
for(int k=1;k<=4;k++)
{
int x=xx[k]+i,y=yy[k]+j;
if(x>=st&&x<=ed&&y>=1&&y<=n&&g[x][y])
{
dp[x][y]=(dp[i][j]+dp[x][y])%mod;
}
}
}
}
}
return dp[ed][tb];
}
// int update(int l,int r)
// {
// for(int i=l;i<=r;i++)
// for(int j=1;j<=n;j++)
// }
int main()
{
speed();
freopen("chess.in","r",stdin);
freopen("chess.out","w",stdout);
cin>>n>>q;
char opt[15];
int x,y;
while(q--)
{
cin>>opt;
if(opt[0]=='A')
{
ed++;
cin>>s+1;
for(int i=1;i<=n;i++)
{
if(s[i]=='.')g[ed][i]=1;
}
}else if(opt[0]=='D')
{
st++;
}else
{
cin>>x>>y;
cout<<solve(x,y)<<endl;
}
}
return 0;
}
T1 题意很容易读假 2-Coloring

如图,考虑一个方案合法,蓝、黄颜色所形成的连通块个数必须 \(\le 2\),否则一定不合法,而显然如果两种颜色连通块个数都为 \(1\) 也不合法,上图以蓝色连通块个数为 \(1\),黄色连通块个数为 \(2\) 为例
洛谷题解
我们要枚举的就是中间分隔开黄左右两部分的点\(A,B\),且\(A,B\)肯定在同一列,因为如果不在,那么必有一列中两个空位不相邻,那我们枚举就是\(O(n^2m)\)的复杂度,用前缀和优化一下,\(O(nm)\),考虑如何计算方案:
接着,也就是说存在一个分割点 \(i\),使得第一个连通块全部在第 \(i\) 列左侧,第二个连通块全部在第 \(i\) 列右侧,那么显然两个连通块与第 \(i\) 列的交点分别是一段不相交区间 \((l_1,r_1),(l_2,r_2)\),我们假设第一个连通块的区间在第二个连通块的区间的上方,也就是如图所示的情况,那么我们假设 \(j=r_1,k=l_2\)(当然如果 \(j=k\) 蓝色连通块会被一分为二,也就是蓝色、黄色连通块个数都为 \(2\) 的情况),那么显然第一个连通块与直线 \(x=i\) 的交中最下方的点的坐标就是 \((j,i)\)(即图中的点 A),第二个连通块与直线 \(x=i\) 的交中最上方的点就是 \((k,i)\)(即图中的点 B)。接下来考虑怎样计算方案数,隔板法是肯定没问题的,不过这里有一种更简便的理解方式,以计算 \(A\) 左上角的方案数为例,它等价于从最左上角的点走到 \(A\) 的方案数,但由于 \(A\) 是这段区间中最下方的点,因此最后一步必须是向下走的,因此左上角的方案数就是从最左上角的点走到 \(A\) 上方的点的方案数,另外四块也同理,如图所示:
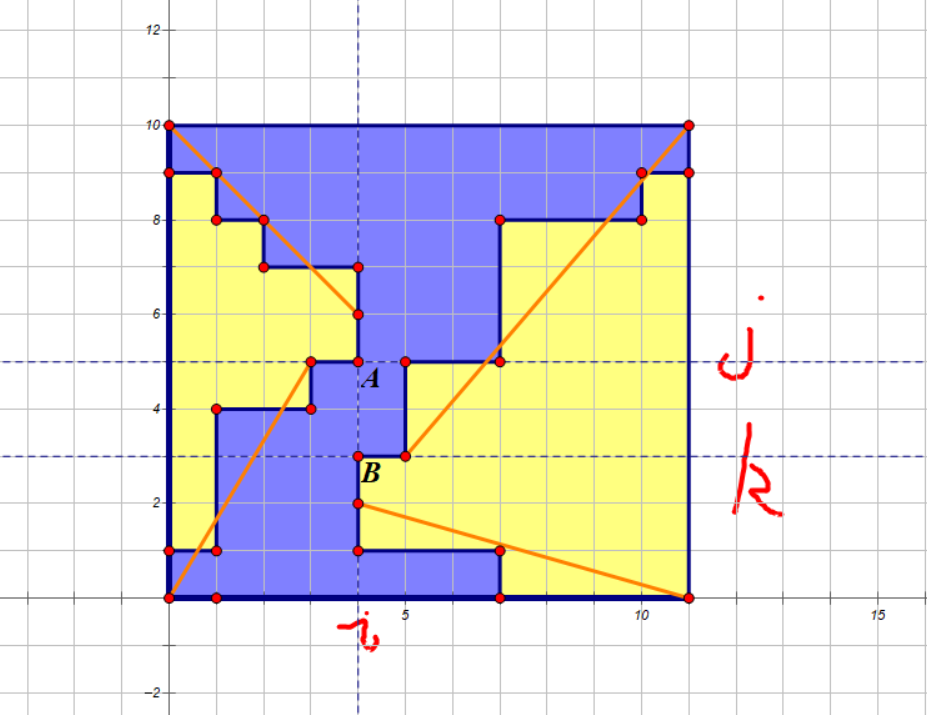
对于 \((l_1,r_1)\) 在 \((l_2,r_2)\) 下方的情况只需乘个 \(2\) 即可,因为所有 \((l_1,r_1)\) 在 \((l_2,r_2)\) 上方的情况把它上下翻转都能够得到 \((l_1,r_1)\) 在 \((l_2,r_2)\) 下方的情况,因此它们构成了一个双射。对于蓝色连通块个数为 \(2\),黄色连通块个数为 \(1\) 的情况其实很 simple,只需做整个网络关于 \(y=x\) 对称的图形即可,但是这样蓝色、黄色连通块个数都是 \(2\) 的情况会被算重,因此第二次计算的时候需要强制令 \(k-j\ge 1\),因为已经考虑过\(A=B\)的情况了,不必再加一遍了
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N = 2e5+5,mod=998244353;
inline int read()
{
int x=0,f=1;char ch=getchar_unlocked();
for(;ch<'0'||ch>'9';ch=getchar_unlocked())ch=='-'?f=-1:f=f;
for(;ch>='0'&&ch<='9';ch=getchar_unlocked())x=(x<<3)+(x<<1)+(ch^48);
return x*f;
}
inline void write(int x)
{
return x<0?(putchar_unlocked('-'),write(-x),void(0)):(x==0?void(0):(write(x/10),putchar_unlocked((x%10)|48),void(0)));
}
ll qpow(ll a,ll b){ll ans=1;while(b){if(b&1)ans=ans*a%mod;b>>=1;a=a*a%mod;}return ans;}
int n,m;ll fac[N],inv[N];
ll ways(int x,int y){return fac[x+y]*inv[x]%mod*inv[y]%mod;}
int main()
{
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
// freopen("magic.in","r",stdin);
// freopen("magic.out","w",stdout);
n=read();m=read();
fac[0]=1;inv[0]=inv[1]=1;
for(ll i=1;i<=N-5;i++)fac[i]=fac[i-1]*i%mod;
for(ll i=2;i<=N-5;i++){
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
// cout<<fac[i]<<endl;
// inv[i]=qpow(fac[i],mod-2);
// cout<<inv[i]<<" "<<qpow(fac[i],mod-2)<<endl;
}
for(ll i=2;i<=N-5;i++)
{
inv[i]=inv[i]*inv[i-1]%mod;
// cout<<inv[i]<<" "<<qpow(fac[i],mod-2)<<endl;
}
ll sum=0,ans=0;
for(int i=1;i<=m-1;i++)
{
sum=0;
for(int j=1;j<=n-1;j++)
{
sum=(sum+ways(i,j-1)*ways(i-1,n-j)%mod)%mod;
ans=(ans+sum*ways(m-i-1,j)%mod*ways(m-i,n-j-1)%mod)%mod;
}
}
n^=m^=n^=m;
for(int i=1;i<=m-1;i++)
{
sum=0;
for(int j=1;j<=n-1;j++)
{
ans=(ans+sum*ways(m-i-1,j)%mod*ways(m-i,n-j-1)%mod)%mod;
sum=(sum+ways(i,j-1)*ways(i-1,n-j)%mod)%mod;
}
}
// cout<<ans<<endl;
write(ans*2%mod);
return 0;
}
T2与P10238 [yLCPC2024] F. PANDORA PARADOXXX 类似
套路:删边维护很困难,所以倒着考虑加边,用并查集维护,
性质:一个连通块树的直径两个端点(深度最深)与另一个连通块树合并时,最长的一定在四个端点之中
求最远点无异于求直径,一个点到最远点的距离一定是到直径某个端点的距离
在维护连通块时,同样可以维护直径,新的直径两个端点一定在原先的4个端点之中
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define pb push_back
#define ull unsigned long long
#define pii pair<int,int>
#define lid (rt<<1)
#define rid (rt<<1|1)
#define ts cout<<"-------------------"<<endl
using namespace std;
const int N = 2e5+5;
int dfn[N],dep[N],f[N][25];
int n,m;vector <pii> edge[N],e;
inline int read()
{
int x=0,f=1;char ch=getchar_unlocked();
for(;ch<'0'||ch>'9';ch=getchar_unlocked())ch=='-'?f=-1:f=f;
for(;ch>='0'&&ch<='9';ch=getchar_unlocked())x=(x<<3)+(x<<1)+(ch^48);
return x*f;
}
inline void write(int x)
{
return x<0?(putchar_unlocked('-'),write(-x),void(0)):(x==0?void(0):(write(x/10),putchar_unlocked((x%10)|48),void(0)));
}
struct Query
{
int op,x;
}q[N];bool vis[N];
void dfs(int u)
{
for(int i=1;i<=20;i++)f[u][i]=f[f[u][i-1]][i-1];
dep[u]=dep[f[u][0]]+1;
for(auto [to,id]:edge[u])
{
if(to==f[u][0])continue;
f[to][0]=u;
dfs(to);
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y])swap(x,y);
for(int i=20;i>=0;i--)
if(dep[f[x][i]]>=dep[y])x=f[x][i];
if(x==y)return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
return f[x][0];
}
int get(int u,int v){return dep[u]+dep[v]-2*dep[lca(u,v)];}
int fa[N];
int find(int x){if(fa[x]!=x)fa[x]=find(fa[x]);return fa[x];}
int ans,res[N],s[N][2],mx[N];
void merge(int u,int v)
{
int fu=find(u),fv=find(v);
// cout<<u<<" "<<v<<" "<<fu<<" "<<fv<<endl;
fa[fu]=fv;
int mm=0;
int now[5]={0,s[fu][0],s[fu][1],s[fv][0],s[fv][1]};
for(int i=1;i<=4;i++)
{
for(int j=i+1;j<=4;j++)
{
// cout<<now[i]<<" "<<now[j]<<" "<<get(now[i],now[j])<<endl;
int dis=get(now[i],now[j]);
if(mm<dis)
{
s[fv][0]=now[i],s[fv][1]=now[j];
mm=dis;mx[fv]=dis;
}
}
}
// cout<<"DAWN"<<fv<<" "<<mx[fv]<<" "<<find(1)<<endl;
ans=max(ans,mx[fv]);
}
int main()
{
speed();
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
freopen("block.in","r",stdin);
freopen("block.out","w",stdout);
// freopen("block1.in","r",stdin);
// freopen("out.out","w",stdout);
int u,v;n=read();m=read();
e.pb({0,0});
for(int i=1;i<=n;i++)fa[i]=i,s[i][0]=s[i][1]=i;
for(int i=1;i<=n-1;i++)
{
u=read();v=read();
edge[u].pb({v,i});edge[v].pb({u,i});
e.pb({u,v});
}
dfs(1);
for(int i=1;i<=m;i++)
{
q[i].op=read();
// cout<<q[i].op<<endl;
q[i].x=read();
if(q[i].op==1)vis[q[i].x]=1;
}
for(int i=1;i<=n-1;i++)
{
if(vis[i])continue;
// cout<<i<<endl;
int x=e[i].first,y=e[i].second;
if(dep[x]>dep[y])swap(x,y);
merge(x,y);
}
for(int i=m;i;i--)
{
if(q[i].op==1)
{
// cout<<q[i].x<<endl;
int x=e[q[i].x].first,y=e[q[i].x].second;
if(dep[x]>dep[y])swap(x,y);
merge(x,y);
}else
{
// cout<<i<<" "<<q[i].x<<" "<<find(q[i].x)<<" "<<mx[find(q[i].x)]<<endl;
int f=find(q[i].x);
int x1=s[f][0],x2=s[f][1];
res[i]=max(res[i],max(get(x1,q[i].x),get(q[i].x,x2)));
}
}
for(int i=1;i<=m;i++)
{
// cout<<i<<endl;
if(q[i].op==2){
res[i]==0?(putchar_unlocked('0'),void(0)):write(res[i]);
putchar_unlocked('\n');
}
}
return 0;
}