题面
给定长度为 $ n $ 的序列:$ a_1, a_2, \cdots , a_n $,记为 \(a[1 \colon n]\)。类似地,\(a[l \colon r]\)( $ 1 \leq l \leq r \leq N$ )是指序列:$ a_{l}, a_{l+1}, \cdots ,a_{r-1}, a_r$。若 \(1\leq l \leq s \leq t \leq r \leq n\),则称 $ a[s \colon t] $ 是 $ a[l \colon r] $ 的子序列。
现在有 $ q $ 个询问,每个询问给定两个数 $ l $ 和 $ r $ ,$ 1 \leq l \leq r \leq n $,求 $ a[l \colon r] $ 的不同子序列的最小值之和。例如,给定序列
$ 5, 2, 4, 1, 3 $,询问给定的两个数为 $ 1 $ 和 $ 3 $,那么 $ a[1 \colon 3] $ 有 $ 6 $ 个子序列 $a[1 \colon 1], a[2 \colon 2], a[3 \colon 3], a[1 \colon 2],a[2 \colon 3], a[1 \colon 3] $,这 $6 $ 个子序列的最小值之和为 \(5+2+4+2+2+2=17\)。
对于 \(100\%\) 的数据, $ 1 \leq n,q \leq 100000$ , $ |a_i| \leq 10^9 $ 。
解析
之前考试遇到过一道叫做“序序”的题,求的是子序列最大值和最小值的积的和。这道题是个丐版,实现起来还是比较简单的。
因为要求所有子序列的和,所以考虑猫树分治。就是把所有询问离线出来,然后挂到树上,找到树上的对应区间段。对于整条询问被这个区间段中点截断的左右两部分递归处理,然后左右合并的部分
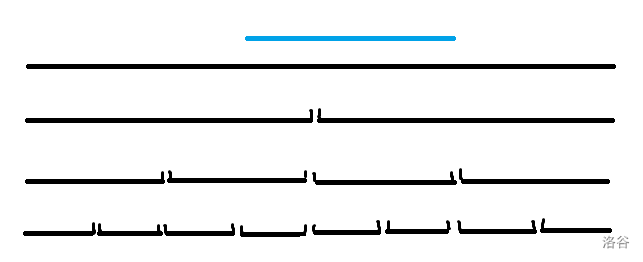
蓝色部分对应的是查询区间,黑色的部分是猫树(?线段树),将查询下放到树上,可以发现被第一层区间的中点截成两半。
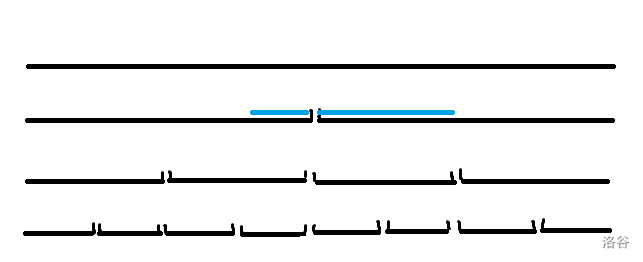
因为被截断的两个区间的答案和本次查询的答案是不影响的,所以被截断的两区间的答案可以继续下放递归处理。 而合并起来后的区间的答案需要在本层计算出来。考虑双指针。
让 \(i\) 从 \(mid\) 向左移,\(j\) 从 \(mid+1\) 向右移,考虑由 \(i\sim j\) 构成的区间的最小值来源于哪里。固定 \(i\),在右边找到一个分界点 \(d\),表示当 \(j\in[mid+1,d-1]\) 时,最小值在左边区间取得,当 \(j\in [d, r]\) 时,最小值在右边区间取得。当 \(i\) 固定下来后,他的 \(d\) 也确定下来,那么就在 \(mid+1\sim d-1\) 的答案里加上 \(min_l\),在 \(d\sim r\) 的答案里加上 \(min_r\)。这个 \(min_r\) 是右区间每个位置对应的最小值,不是固定的,区间修,区间查,需要用到线段树。因为不同的两种加值对应的系数也不同,所以需要开两棵线段树。并且随着 \(i\) 左移,\(d\) 的位置是单调向右的。所以单次维护复杂度 \(\mathcal{O}(len\log len)\)。总复杂度 \(\mathcal{n\log^2n}\)。
code
#include<bits/stdc++.h>
using namespace std;
#ifdef _WIN32
#define getchar _getchar_nolock
#define putchar _putchar_nolock
#else
#define getchar getchar_unlocked
#define putchar putchar_unlocked
#endif
template <typename T> inline void rd(T &x){
x = 0; int f = 1; char ch = getchar();
while(!isdigit(ch)){ if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) x = (x<<1) + (x<<3) + (ch^48), ch = getchar();
x *= f;
}
template <typename T> inline void wt(T x){
if(x < 0) putchar('-'), x = -x;
if(x / 10 > 0) wt(x / 10); putchar(x % 10 + '0');
}
#define int long long
#define ls (id << 1)
#define rs (id << 1 | 1)
constexpr int N = 1e5 + 5;
int n, q, a[N], ans[N], sum[N<<2], jmn[N], s[N];
struct Seg{ int l, r, ai; };
vector<Seg> spl[N<<2]; vector<int> ful[N<<2];
inline void insert(int id, int l, int r, int x, int y, int ai){
if(l > r) return ;
if(x <= l && r <= y) return (void)(ful[id].push_back(ai));
int mid = (l + r) >> 1;
if(x <= mid && mid < y) spl[id].push_back(Seg{max(l, x), min(r, y), ai});
if(x <= mid) insert(ls, l, mid, x, y, ai);
if(y > mid) insert(rs, mid+1, r, x, y, ai);
}
namespace ST{
struct node{ int l, r, sum[2], tag[2], val[2]; }t[N<<2];
inline void pushup(int id){
t[id].sum[0] = t[ls].sum[0] + t[rs].sum[0];
t[id].sum[1] = t[ls].sum[1] + t[rs].sum[1];
}
inline void addtag(int id, int k, int p){
t[id].tag[p] += k; t[id].sum[p] += k * t[id].val[p];
}
inline void pushdown(int id){
if(t[id].tag[0]) addtag(ls, t[id].tag[0], 0), addtag(rs, t[id].tag[0], 0);
if(t[id].tag[1]) addtag(ls, t[id].tag[1], 1), addtag(rs, t[id].tag[1], 1);
t[id].tag[0] = t[id].tag[1] = 0;
}
inline void build(int id, int l, int r){
t[id].l = l, t[id].r = r; t[id].val[0] = t[id].val[1] = 0;
t[id].sum[0] = t[id].sum[1] = t[id].tag[0] = t[id].tag[1] = 0;
if(l == r) return (void)(t[id].val[1] = jmn[l], t[id].val[0] = 1);
int mid = (l + r) >> 1;
build(ls, l, mid), build(rs, mid+1, r);
t[id].val[0] = t[ls].val[0] + t[rs].val[0];
t[id].val[1] = t[ls].val[1] + t[rs].val[1];
pushup(id);
}
inline void modify(int id, int l, int r, int k, int p){
if(l > r) return;
if(l <= t[id].l && t[id].r <= r) return addtag(id, k, p);
pushdown(id); int mid = (t[id].l + t[id].r) >> 1;
if(l <= mid) modify(ls, l, r, k, p);
if(r > mid) modify(rs, l, r, k, p);
pushup(id);
}
inline int query(int id, int l, int r){
if(l <= t[id].l && t[id].r <= r) return t[id].sum[0] + t[id].sum[1];
pushdown(id); int mid = t[ls].r, as = 0;
if(l <= mid) as += query(ls, l, r);
if(r > mid) as += query(rs, l, r);
return as;
}
}
inline void mao(int id, int l, int r){
if(l == r){
sum[id] = a[l];
for(int it : ful[id]) ans[it] += sum[id];
return;
}
int mid = (l + r) >> 1, imn = a[mid], j = mid + 1, k = 0;
sort(spl[id].begin(), spl[id].end(), [](const Seg x, const Seg y){ return x.l > y.l; });
jmn[mid + 1] = a[mid + 1]; s[mid + 1] = a[mid + 1];
for(int i=mid+2; i<=r; ++i) jmn[i] = min(a[i], jmn[i-1]);
ST::build(1, mid + 1, r);
for(int i=mid; i>=l ;--i){
imn = min(imn, a[i]); while(j <= r && jmn[j] > imn) ++j;
ST::modify(1, mid+1, j - 1, imn, 0), ST::modify(1, j, r, 1, 1);
while(k < (int)spl[id].size() && spl[id][k].l == i) ans[spl[id][k].ai] += ST::query(1, mid+1, spl[id][k].r), ++k;
}
sum[id] += ST::query(1, mid+1, r);
mao(ls, l, mid), mao(rs, mid+1, r);
sum[id] += sum[ls] + sum[rs];
for(int it : ful[id]) ans[it] += sum[id];
}
signed main(){
rd(n), rd(q);
for(int i=1; i<=n; ++i) rd(a[i]);
for(int i=1, x, y; i<=q; ++i) rd(x), rd(y), insert(1, 1, n, x, y, i);
mao(1, 1, n); for(int i=1; i<=q; ++i) wt(ans[i]), putchar('\n');
return 0;
}