JOISC2020 Day 4 A 首都
考虑一条链的情形。
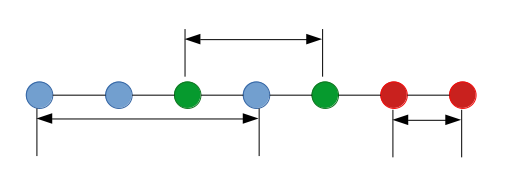
如图,将每个城市视为一条线段,容易发现交错(有交但不包含)的若干线段必须全部合并才能符合条件。但如果这么写会出错,原因是线段有包含关系,外层线段需要统计内层线段的答案,但内层线段不需要统计外层线段的答案。如果设内层线段为 \(x\),外层线段为 \(y\),则可以这样描述:
- 如果选 \(x\) 作为首都,则不能选 \(y\)(选 \(y\) 一定更劣);
- 如果选 \(y\) 作为首都,则必须选 \(x\)(满足作为首都的条件)。
这很像 2-SAT 问题,启发我们根据依赖关系建图:如果城市 \(a\) 的两个城镇之间的路径经过城市 \(b\),则连边 \(a \rightarrow b\)。答案即为没有出边(满足条件不依赖于合并更多城市)的最小的强连通分量的大小减 \(1\)。
暴力连边一定会超时,考虑优化建图:若当前对于城市 \(x\) 建图,类似于建虚树,取出 \(x\) 的所有城镇以及它们的所有 LCA 作为关键点。关键点之间使用树链剖分得到一段连续的链,将 \(x\) 向链上的点所属的城市分别连边。
使用 线段树优化建图,在树剖得到的 DFS 序上建立线段树,每个叶子节点代表向其代表的原树上的点所属的城市连边,线段树内部父亲向儿子连边。如此操作后,每条链 \([l, r]\) 均可分解为至多 \(O(\log n)\) 个极大区间。可以发现,新图一定与原图等价,但边的数量减小为可接受级别。
求强连通分量使用 Tarjan。
时间复杂度 \(O(n \log^2 n)\)。
#include <algorithm>
#include <iostream>
#include <set>
#include <vector>
using namespace std;
int n, k, rt;
int c[1000005];
vector<int> vec[1000005];
vector<int> G[1000005];
vector<int> include[1000005];
int f[1000005];
int dfn[1000005], dfn_clock;
int nfd[1000005];
int dep[1000005];
int son[1000005];
int top[1000005];
int siz[1000005];
static inline void dfs(int u, int fa) { // chain segmentation
f[u] = fa;
dep[u] = dep[fa] + 1;
siz[u] = 1;
for (auto v : vec[u]) {
if (v == fa)
continue;
dfs(v, u);
siz[u] += siz[v];
if (siz[v] > siz[son[u]])
son[u] = v;
}
}
static inline void dfs2(int u) {
dfn[u] = ++dfn_clock;
nfd[dfn_clock] = u;
if (!son[u])
return;
top[son[u]] = top[u];
dfs2(son[u]);
for (auto v : vec[u]) {
if (v == f[u] || v == son[u])
continue;
top[v] = v;
dfs2(v);
}
}
static inline int LCA(int u, int v) {
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]])
swap(u, v);
u = f[top[u]];
}
if (dep[u] < dep[v])
return u;
return v;
}
struct node { // SGT optimize building graph
int ls, rs;
} d[4000005];
int cnt;
static inline int build(int s, int t) {
int p = ++cnt;
if (s == t) {
G[p].push_back(c[nfd[s]]);
return p;
}
int mid = (s + t) >> 1;
d[p].ls = build(s, mid);
d[p].rs = build(mid + 1, t);
G[p].push_back(d[p].ls);
G[p].push_back(d[p].rs);
return p;
}
static inline void addedge(int l, int r, int s, int t, int from, int p) {
if (l <= s && r >= t) {
G[from].push_back(p);
return;
}
int mid = (s + t) >> 1;
if (l <= mid)
addedge(l, r, s, mid, from, d[p].ls);
if (r > mid)
addedge(l, r, mid + 1, t, from, d[p].rs);
}
static inline void add(int u, int v) {
int col = c[u];
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]])
swap(u, v);
addedge(dfn[top[u]], dfn[u], 1, n, col, rt);
u = f[top[u]];
}
if (dep[u] > dep[v])
swap(u, v);
addedge(dfn[u], dfn[v], 1, n, col, rt);
}
int t_dfn[1000005], t_low[1000005], t_dfn_clock;
int sta[1000005], tail;
bool insta[1000005];
vector<int> scc[1000005];
int belong[1000005];
int scc_cnt;
static inline void tarjan(int u) {
t_dfn[u] = t_low[u] = ++t_dfn_clock;
sta[++tail] = u;
insta[u] = true;
for (auto v : G[u]) {
if (!t_dfn[v]) {
tarjan(v);
t_low[u] = min(t_low[u], t_low[v]);
} else if (insta[v])
t_low[u] = min(t_low[u], t_dfn[v]);
}
if (t_dfn[u] == t_low[u]) {
++scc_cnt;
while (sta[tail] != u) {
scc[scc_cnt].push_back(sta[tail]);
belong[sta[tail]] = scc_cnt;
insta[sta[tail]] = false;
--tail;
}
scc[scc_cnt].push_back(u);
belong[u] = scc_cnt;
insta[u] = false;
--tail;
}
}
int sum[1000005];
int deg[1000005];
signed main() {
#ifndef ONLINE_JUDGE
freopen("P7215.in", "r", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> n >> k;
cnt = k;
for (int i = 1; i < n; ++i) {
int u, v;
cin >> u >> v;
vec[u].push_back(v);
vec[v].push_back(u);
}
for (int i = 1; i <= n; ++i) {
cin >> c[i];
include[c[i]].push_back(i);
}
dfs(1, 0);
top[1] = 1;
dfs2(1);
rt = build(1, n);
for (int i = 1; i <= k; ++i) {
if (include[i].size() > 1) { // like virtual tree
int cur = include[i][0];
for (size_t j = 1; j < include[i].size(); ++j) {
int lca = LCA(include[i][0], include[i][j]);
if (include[i][j] != lca)
add(include[i][j], lca);
if (dep[lca] < dep[cur])
cur = lca;
}
if (include[i][0] != cur)
add(include[i][0], cur);
}
}
for (int i = 1; i <= cnt; ++i)
if (!t_dfn[i])
tarjan(i);
for (int i = 1; i <= k; ++i)
++sum[belong[i]];
for (int u = 1; u <= cnt; ++u)
for (auto v : G[u])
if (belong[u] != belong[v])
++deg[belong[u]];
int ans = 1e9;
for (int i = 1; i <= k; ++i)
if (!deg[belong[i]])
ans = min(ans, sum[belong[i]]);
cout << ans - 1 << endl;
return 0;
}