8.11 Epic Round Augest 2024 (Div.1 + Div.2)

Solve : A~C+E+F1 (4.5/8)

Rank : 463

Rating : \(2116+58=2174\)

Perf : 2348

发挥评价 : Normal

这场排名比上次低，但是 Perf 比上次高，怎么回事呢。

不过还是降智了没搞出来 D，但凡冲出来 D1 都可以进 300 名并获得 Grandmaster 的 Performance。

申明：我的 Performance 采用简单的 \(Current Rating+\Delta\times 3\) 的计算方式，其跟实际数据会根据当前 Rating 有较小的误差，不过 CF 这个计算本来就迷，就先采用这个近似方案。

CF2002D1 / D2

给定一棵有根树和一个排列，加上 \(q\) 次操作，每次交换排列中两个数，问每次操作后，序列是否是树的一个合法 dfs 序。

\(n\le 3\times 10^5,q\le 10^5\)，简单版中树是一棵满二叉树。

这种题目一般都是找充要条件的……

例如本题，有一个较明显的条件是：如果每个点 \(u\) 后面的 \(size_u\) 个点正好都是它在树上子树里的那些点，就可以，然后这个可以用刚学的和哈希搞定，由于修改一个点必须回到它的根，只能通过 D1。

D2 的话还要深挖一些性质。

结果完全忘掉了总长 \(2n-2\) 这个，想都没往这想。

然后再加上啥后面不能是前面祖先，前面不能是后面超过一级的祖先，如果下一个不是儿子这个必是根啥的，就行了。

史，根本不写！

CF2002E

一个序列，每次消掉所有极长连续相等段的第一个数，问多少秒消完。

现在序列初始为空动态添加 \(n\) 次，每次在末尾加入 \(a_i\) 个 \(b_i\)，每次加入都回答一次这个问题。

\(n,b_i\le 10^5,a_i\le 10^9\)。

Solution：第一反应是 \(\max a_i\)，但是不对，因为后面可能跟前面相等数合并，合并之后两段合起来消一个数，时间会变长。

然后发现两端能合并当且仅当中间都比他们短，而且一旦合并了，中间就没有意义了，不可能再合并或者影响答案的。

另外如果后添加的比前面的多，前面也不可能合并了，也没必要留着了。

于是想到维护单调栈，这题就结束了。

具体的，维护一个数量依次递减的单调栈，每次从最后一个一个把栈顶不同色且更小的弹出，碰到同色就吸收，具体的，设现在加入的数量为 \(a\)，栈顶同色的为 \(x\)，刚刚弹出的异色栈顶为 \(y\)，则合并为 \(a+x-y\) 继续下传。

每次答案就是栈底。

CF2002F1 / F2

考虑一个初始为 \((0,0)\) 的点对，每次可以选择一个数加 \(1\)，但是点对全程要满足：

1. \(\gcd(x,y)=1\)（我们认为 \(gcd(0,x)=x\)）

2. \(x\le n,y\le m\)

现在给定 \(l,f\)，请合法操作以最大化 \(xl+yf\)，输出最大值即可。

\(n,m\le 2\times 10^7,l,f\le 10^9\)，简单版 \(n=m\)。

现在我们先打个表，我们发现，比较优的策略是先把数对调到 \((1,p)\)（小于等于 \(n\) 最大的质数），此时另一个数可以随意到达 \(1\) 到 \(p-1\)。

发现任何路径都肯定要经过这两条线。另外又发现当我到达 \((q,p)\)（\(q\) 为小于等于 \(n\) 次大的质数）的时候，由于一般来说 \(2q>n\)（较小时候不一定，所以 \(n\le 20\) 时候可以直接暴力 BFS）

所以顺着走到 \((q,n)\) 都可以。

画个图：

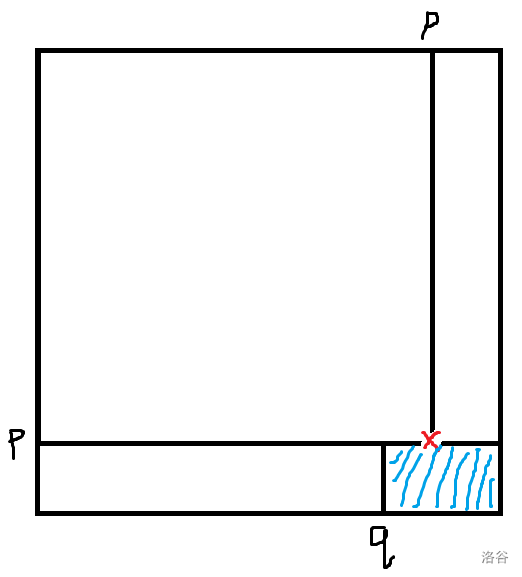
那么，答案显然会在蓝色阴影区域内。

实际上呢，你发现蓝色根本不大，直接暴力建一下跑个 BFS 就行了。

我会说我以为 BFS 写挂了吃了两发吗

F2 还不会，你先别急。