今天学了字符产的第一部分:
- 反转字符串,使用双指针。
- 反转字符串Ⅱ,需要固定规律一段一段去处理字符串的时候,要想想在在for循环的表达式上做做文章。
- 数组填充问题,其做法都是先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
1. 反转字符串
题目:编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
和反转链表一样,使用双指针解决问题。但是比链表更简单,字符串明显可以知道长度,所以开头一个结尾一个,两两交换即可。
void reverseString(vector<char>& s) {
for (int i = 0, j = s.size() - 1; i < s.size()/2; i++, j--) {
swap(s[i],s[j]);
}
}
2. 反转字符串Ⅱ
题目:给定一个字符串 s 和一个整数 k,从字符串开头算起, 每计数至 2k 个字符,就反转这 2k 个字符中的前 k 个字符。
如果剩余字符少于 k 个,则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
输入: s = "abcdefg", k = 2
输出: "bacdfeg"
每次看2k个,因此在遍历字符串的过程中,只要让 i += (2 * k),i 每次移动 2 * k 就可以了,然后判断是否需要有反转的区间。
当需要固定规律一段一段去处理字符串的时候,要想想在在for循环的表达式上做做文章。
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += (2 * k)) {
// 1. 每隔 2k 个字符的前 k 个字符进行反转
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
if (i + k <= s.size()) {
reverse(s.begin() + i, s.begin() + i + k );
} else {
// 3. 剩余字符少于 k 个,则将剩余字符全部反转。
reverse(s.begin() + i, s.end());
}
}
return s;
}
若是自己实现reverse,和上头第一题的思路一样:
class Solution {
public:
void reverse(string& s, int start, int end) {
for (int i = start, j = end; i < j; i++, j--) {
swap(s[i], s[j]);
}
}
string reverseStr(string s, int k) {
for (int i = 0; i < s.size(); i += (2 * k)) {
// 1. 每隔 2k 个字符的前 k 个字符进行反转
// 2. 剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符
if (i + k <= s.size()) {
reverse(s, i, i + k - 1);
continue;
}
// 3. 剩余字符少于 k 个,则将剩余字符全部反转。
reverse(s, i, s.size() - 1);
}
return s;
}
};
3. 替换数字
题目:给定一个字符串 s,它包含小写字母和数字字符,请编写一个函数,将字符串中的字母字符保持不变,而将每个数字字符替换为number。
例如,对于输入字符串 "a1b2c3",函数应该将其转换为 "anumberbnumbercnumber"。
直接的想法是再开一个数组,根据遍历到的原始数组中的内容,往新数组里填内容。但是,为了不使用额外空间,可以选择:
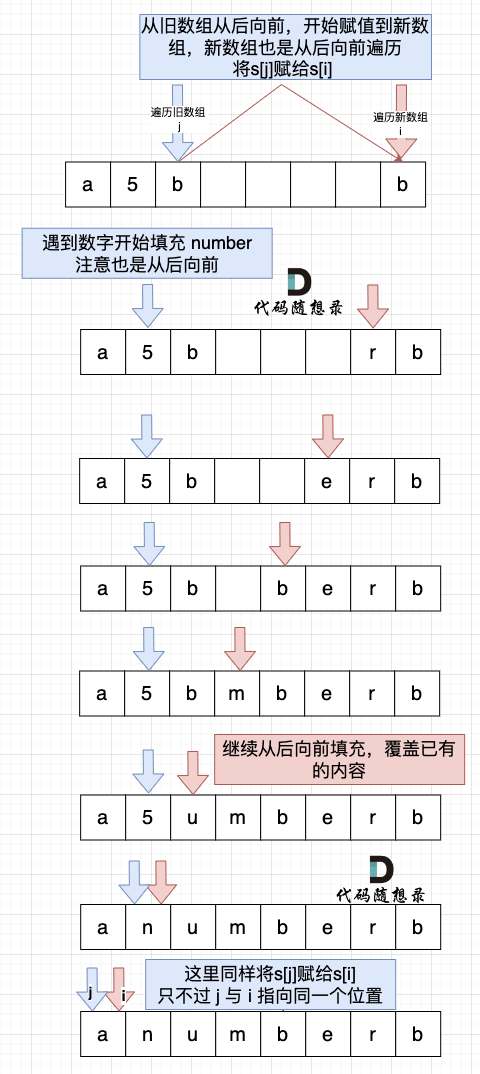
很多数组填充类的问题,其做法都是先预先给数组扩容带填充后的大小,然后在从后向前进行操作。
s.resize(s.size() + count * 5);resize的用法。
这么做有两个好处:
- 不用申请新数组。
- 从后向前填充元素,避免了从前向后填充元素时,每次添加元素都要将添加元素之后的所有元素向后移动的问题。
#include <iostream>
using namespace std;
int main() {
string s;
while (cin >> s) {
int sOldIndex = s.size() - 1;
int count = 0; // 统计数字的个数
for (int i = 0; i < s.size(); i++) {
if (s[i] >= '0' && s[i] <= '9') {
count++;
}
}
// 扩充字符串s的大小,也就是将每个数字替换成"number"之后的大小
s.resize(s.size() + count * 5);
int sNewIndex = s.size() - 1;
// 从后往前将数字替换为"number"
while (sOldIndex >= 0) {
if (s[sOldIndex] >= '0' && s[sOldIndex] <= '9') {
s[sNewIndex--] = 'r';
s[sNewIndex--] = 'e';
s[sNewIndex--] = 'b';
s[sNewIndex--] = 'm';
s[sNewIndex--] = 'u';
s[sNewIndex--] = 'n';
} else {
s[sNewIndex--] = s[sOldIndex];
}
sOldIndex--;
}
cout << s << endl;
}
}
今日古诗
促拍丑奴儿 乡邻会饮,有请予增损旧曲者,
金朝 元好问
无物慰蹉跎。
占一丘、一壑婆娑。
闲来点检平生事,天南地北,几多尘土,何限风波。
花坞与松坡。
尽先生、少小经过。
老来诗酒犹堪任,家山在眼,亲朋满坐,不醉如何。