?p=22251

原文出处：拓端数据部落公众号

归一化数据是数据科学中的一项常见任务。有时它可以让我们加快梯度下降的速度或提高模型的准确性，在某些情况下，它绝对是至关重要的。

【视频】逆变换抽样将数据标准化和R语言结构化转换：BOX-COX、凸规则变换方法

逆变换抽样将数据标准化和R语言结构化转换：BOX-COX、凸规则变换方法

一些归一化技术，如取对数，在大多数情况下可能有效，但在这种情况下，我决定尝试对任何数据都有效的方法，不管它最初是如何分布的。我下面要介绍的方法是基于逆变换抽样：主要思想是根据数据的统计特性，构造这样的函数F，所以F(x)是正态分布。下面是如何做的。

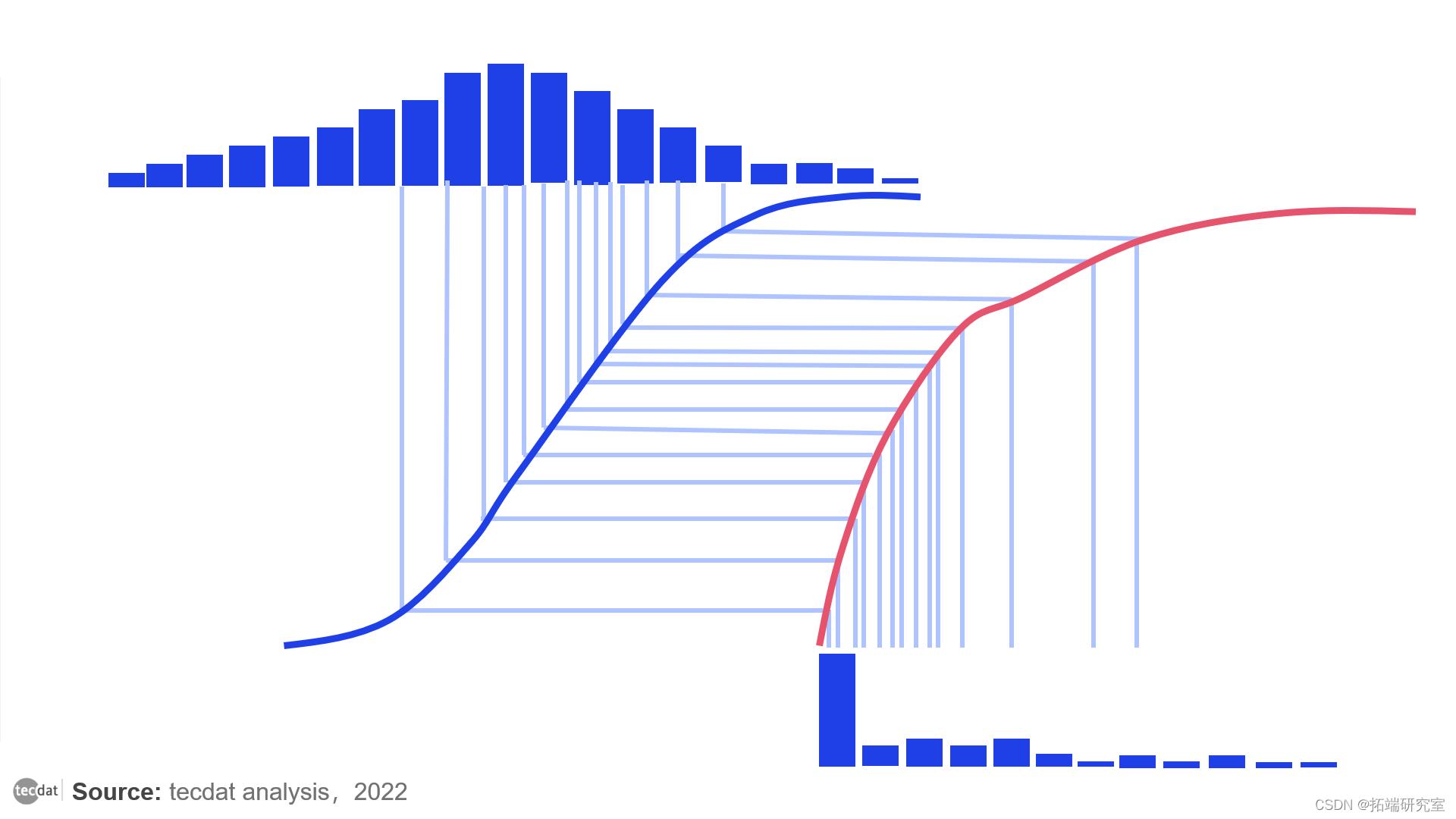
我所说的算法是基于逆变换抽样法。这种方法被广泛用于伪随机数生成器，从任何给定的分布中生成数字。有了均匀分布的数据，你总是可以把它转化为分布，有任何给定的累积密度函数（或简称CDF）。CDF显示了分布的数据点中有多大比例小于给定值，基本上表示了分布的所有统计特性。

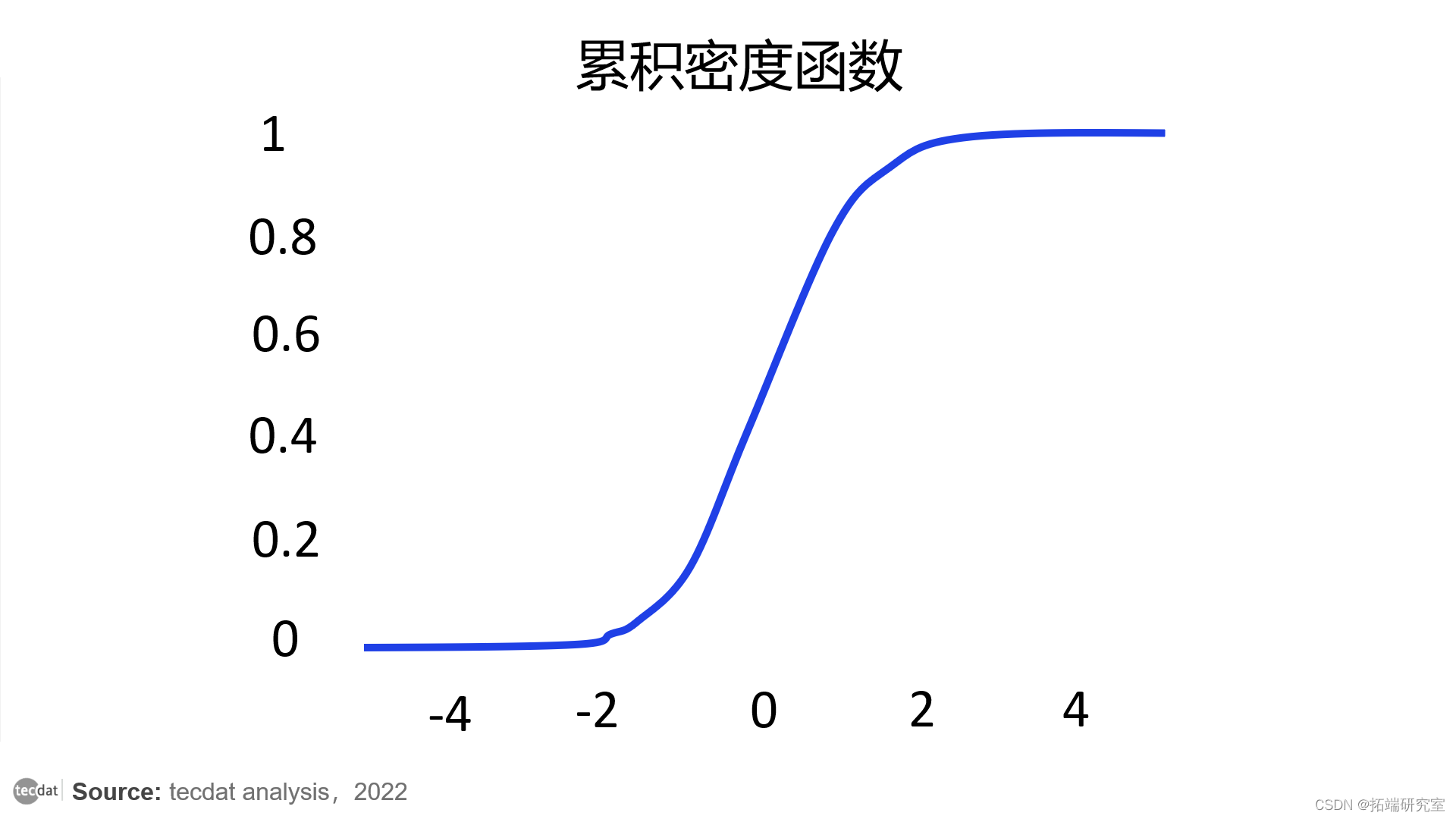
具有零平均数和单位方差的正态分布的CDF。它显示，几乎所有的点都大于-4，小于4，其中50%的点小于0

其主要思想是，对于任何连续分布的数据xᵢ，CDF(xᵢ)是均匀分布的。换句话说，要想得到均匀分布的数据，只需取每个点的CDF。这句话的数学证明超出了本文的范围，但是上述操作本质上只是对所有数值进行排序，并将每个数值替换为其数字，这给了它一个直观的感觉。

将一些混乱的数据转化为统一的数据

在上面的图中，你可以看到它是如何工作的。我生成了一些混乱的分布数据，然后计算了它的CDF（红线），并用它转换了数据。现在数据是均匀分布的。

计算CDF比它看起来更容易。记住，CDF是比给定数据小的一部分。

一般来说，CDF是一个双射函数，这意味着转换是可逆的。我们可以利用这一事实将得到的均匀分布转化为我们想要的任何分布，例如正态分布。为了做到这一点，我们需要计算我们想得到的分布的反CDF。一般来说，这不是最简单的任务。我们需要的函数被称为百分点函数，简称PPF。幸运的是，任何主要分布的PPF都可以通过SciPy库获得，人们不需要自己去计算它。

具有零平均数和单位方差的正态分布的PPF。它显示第50个百分位数是0，超过60%的点位于-1和1之间。

下面是对它的解释：对于0和1之间的任何参数x，PPF返回点适合x'th百分位的最大值。同时，作为CDF的反函数，它看起来像第一张图片中的函数，只是旋转了90°。

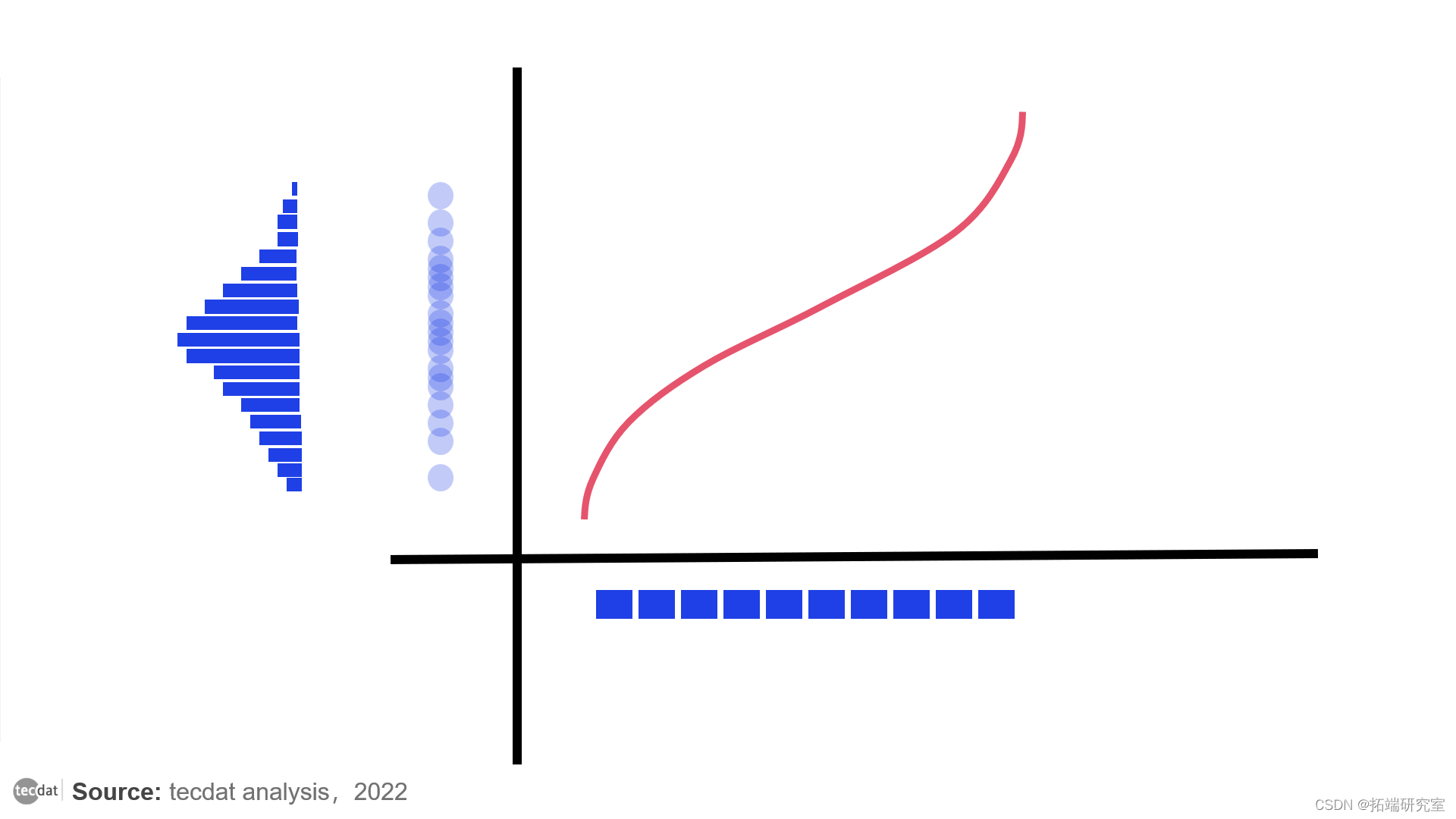
从均匀分布中获得正态分布

现在我们有了一个漂亮的正态分布，如愿以偿。最后，要做一个函数来转换我们的初始数据，我们所要做的就是把这两个操作合并到一个函数中。

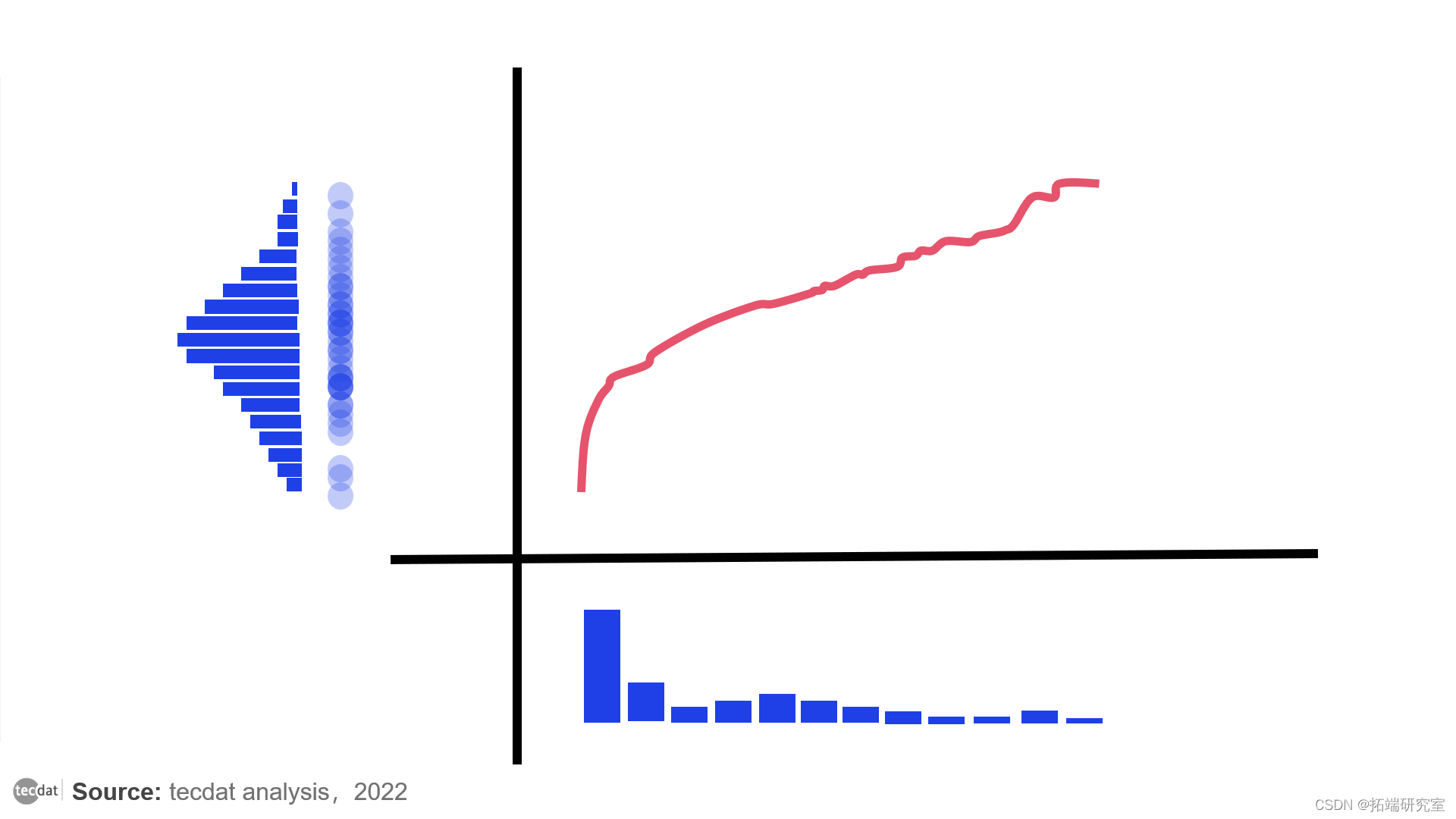
将初始杂乱的分布转化为均值为零、方差为单位的正态分布

上图中的红线代表最终的变换函数。

请注意，最后的变换总是单调的。这意味着没有两个点在转换后被调换。如果一个点的初始特征值大于另一个点的初始特征值，在转换之后，转换后的值对该点来说也会更大。这一事实使得该算法可以应用于数据科学任务。

总而言之，与更常见的方法不同，本文描述的算法不需要对初始分布进行任何假设。同时，输出的数据极其精确地遵循正态分布。这种方法已被证明可以提高模型的准确性，这些模型假定输入数据分布。

R语言进行数据结构化转换：Box-Cox变换、“凸规则”变换方法

全文链接：http://tecdat.cn/?p=22251

原文出处：拓端数据部落公众号

R语言进行数据结构化转换：Box-Cox变换、“凸规则”变换方法

线性回归时若数据不服从正态分布，会给线性回归的最小二乘估计系数的结果带来误差，所以需要对数据进行结构化转换。

在讨论回归模型中的变换时，我们通常会简单地使用Box-Cox变换，或局部回归和非参数估计。

这里的要点是，在标准线性回归模型中，我们有

但是有时候，线性关系是不合适的。一种想法可以是转换我们要建模的变量，然后考虑

这就是我们通常使用Box-Cox变换进行的操作。另一个想法可以是转换解释变量，

例如，我们有时会考虑连续的分段线性函数，也可以考虑多项式回归。

“凸规则”变换

“凸规则”(Mosteller. F and Tukey, J.W. (1978). Data Analysis and Regression)的想法是，转换时考虑不同的幂函数。

1.“凸规则”为纠正非线性的可能变换提供了一个起点。
2 .通常情况下，我们应该尝试对解释变量进行变换，而不是对因变量Y进行变换，因为Y的变换会影响Y与所有X的关系，而不仅仅是与非线性关系的关系
3.然而，如果因变量是高度倾斜的，那么将其转换为以下变量是有意义的

更具体地说，我们将考虑线性模型。

根据回归函数的形状（上图中的四个曲线，在四个象限中），将考虑不同的幂。

例如让我们生成不同的模型，看看关联散点图。

> plot(MT(p=.5,q=2),main="(p=1/2,q=2)")
> plot(MT(p=3,q=-5),main="(p=3,q=-5)")
> plot(MT(p=.5,q=-1),main="(p=1/2,q=-1)")
> plot(MT(p=3,q=5),main="(p=3,q=5)")

如果我们考虑图的左下角部分，要得到这样的模式，我们可以考虑

或更一般地

其中和都大于1.并且越大，回归曲线越凸。

让我们可视化数据集上的双重转换，例如cars数据集。

> tukey=function(p=1,q=1){
+ regpq=lm(I(y^q)~I(x^p) )
+ u=seq(min(min( x)-2,.1),max( x)+2,length=501)
+ polygon(c(u,rev(u)),c(vic[,2],rev(vic[,3]))^(1/q)
+ lines(u,vic[,2]^(1/q)
+ plot(x^p, y^q )
+ polygon(c(u,rev(u))^p,c(vic[,2],rev(vic[,3])) )
+ lines(u^p,vic[,2])

例如，如果我们运行

> tukey(2,1)

我们得到如下图，

左侧是原始数据集，右侧是经过转换的数据集，其中有两种可能的转换。在这里，我们只考虑了汽车速度的平方（这里只变换了一个分量）。在该转换后的数据集上，我们运行标准线性回归。我们在这里添加一个置信度。然后，我们考虑预测的逆变换。这条线画在左边。问题在于它不应该被认为是我们的最佳预测，因为它显然存在偏差。请注意，在这里，有可能考虑另一种形状相同但完全不同的变换