LeetCode 864. Shortest Path to Get All Keys

原题链接在这里：https://leetcode.com/problems/shortest-path-to-get-all-keys/description/

题目：

You are given an m x n grid grid where:

• '.' is an empty cell.
• '#' is a wall.
• '@' is the starting point.
• Lowercase letters represent keys.
• Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

Example 1:

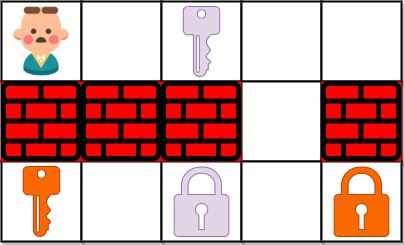
Input: grid = ["@.a..","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

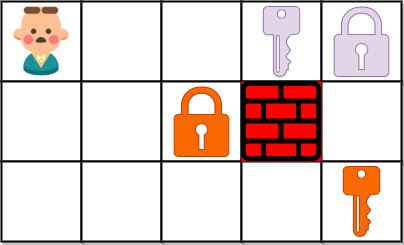
Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 30
• grid[i][j] is either an English letter, '.', '#', or '@'. 
• There is exactly one '@' in the grid.
• The number of keys in the grid is in the range [1, 6].
• Each key in the grid is unique.
• Each key in the grid has a matching lock.

题解：

The question asks for shortest path to find all the keys. When it is shortest path, we need to use BFS.

We maintain the state of the keys we already found, since we need it to know if we can open the lock we meet.

We use a integer to maintain the state of keys we already found. Each digit is 0, 1, representing if we see this key. 'a' is the last digit, 'b' is the second last digit.

In the BFS node, we need to have the coordinate x and y. Also we need to keys state.
Also we need to maintain a similar visited set for it.

Time Complexity: O(m * n * 2^k). m = grid.length. n = grid[0].length(). k is the number of keys. Since for each cell in the grid, there could be 2 ^ k possible key combinations.

Space: O(m * n * 2^k).

AC Java:

 1 class Solution {
 2     int[][] dirs = new int[][]{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
 3     public int shortestPathAllKeys(String[] grid) {
 4         int m = grid.length;
 5         int n = grid[0].length();
 6         int[] start = new int[3];
 7         int keys = 0;
 8         for(int i = 0; i < m; i++){
 9             for(int j = 0; j < n; j++){
10                 char c = grid[i].charAt(j);
11                 if(c == '@'){
12                     start[0] = i;
13                     start[1] = j;
14                 }else if(c >= 'a' && c <= 'z'){
15                     keys |= (1 << (c - 'a'));
16                 }
17             }
18         }
19 
20         LinkedList<int[]> que = new LinkedList<>();
21         HashSet<String> visited = new HashSet<>();
22         visited.add(start[0] + "," + start[1] + "," + start[2]);
23         que.add(start);
24 
25         int level = 0;
26         while(!que.isEmpty()){
27             int size = que.size();
28             while(size-- > 0){
29                 int[] cur = que.poll();
30                 if(cur[2] == keys){
31                     return level;
32                 }
33 
34                 for(int [] dir : dirs){
35                     int x = cur[0] + dir[0];
36                     int y = cur[1] + dir[1];
37                     int k = cur[2];
38                     if(x < 0 || x >= m || y < 0 || y >= n || grid[x].charAt(y) == '#'){
39                         continue;
40                     }
41 
42                     char c = grid[x].charAt(y);
43                     if(c >= 'A' && c <= 'Z' && ((k >> (c - 'A')) & 1) == 0){
44                         // no key yet
45                         continue;
46                     }
47 
48                     if(c >= 'a' && c <= 'z'){
49                         // found a key, update the key state
50                         k = k | (1 << (c - 'a'));
51                     }
52 
53                     String state = x + "," + y + "," + k;
54                     if(visited.contains(state)){
55                         continue;
56                     }
57 
58                     visited.add(state);
59                     que.add(new int[]{x, y, k});
60                 }
61             }
62 
63             level++;
64         }
65 
66         return -1;
67     }
68 }