2024夏令营提高1模考0718模拟赛(提高1)补题报告
$$
0718模拟赛(提高1) \ \ 补题报告 \ 2024年7月18日 \ by \ \ \ 唐一潇
$$
一、做题情况
-
第一题比赛 $100 / 100$ ,赛后通过
-
第二题比赛 $0 / 100$ ,赛后通过
-
第三题比赛 $0 / 100$ ,赛后通过
-
第四题比赛 $0/ 100$ ,赛后通过
-
比赛得分 $100 / 400$ ,赛后补题 $400$ / $400$
二、比赛概况
T1AC用二分,太简单了。
T2本来想骗分输出
-1但是这好像构造了每一组数据都有合法解。T3太难了,虽然知道是KMP,但是不知道怎么做。
T4链式没分,正解是线段树,暴力RE了。
三、题解报告
T1:旅行
题面:
时间限制: 1000ms
空间限制: 524288kB
题目描述
鱼大大计划环华夏自驾游游玩一圈,在他的计划中,这次旅行将在m天内完成,预计游玩n个城市,每个城市游玩x天,然后赶路开车以均速去到下一个城市,现鱼大大从海洋城市出发,按游玩顺序先后给出每个城市和上一个城市之间的距离(km),问鱼大大每天至少赶路多少距离(km)才能在m天内游玩所有城市?
输入格式
第一行两个数字n,m;分别表示要游玩的城市数量和游玩天数
接下来n行,每行两个整数ai,x,ai表示第i个城市和第i−1个城市之间的距离(km);x表示在第i个城市游玩的时间(天);i=1时为第一个游玩城市与鱼大大的出发地海洋城市的距离
注: 每天赶路的距离为整数输出格式
一个整数表示鱼大大每天赶路的最少距离。如果无法再预计时间完成输出-1.
样例
Input 1
3 21
225 1
675 1
450 1Output 1
75
样例解释
鱼大大从海洋城市出发,要在21天游玩完毕这3个城市。需每天最少赶路75km。
从海洋城市到第一城225km,需要赶路3天,游玩1天;
从第一城到第二城675km,需要赶路9天,游玩1天;
从第二城到第三城450km,需要赶路6天,游玩1天;
共21天。
若赶路距离再少,则无法在21天内完成。数据范围
$1≤n≤10^5$
$1≤a_i,m≤10^{15}$做法:
-
理解问题:鱼大大需要在 $m$ 天内游玩 $n$ 个城市,每个城市游玩x天,并且需要在城市之间赶路。我们需要计算每天至少需要赶路多少距离。
-
计算总游玩天数:总游玩天数为$∑^n_{i=1}x_{i}$。
-
计算总赶路天数:总赶路天数为$m-∑^n_{i=1}x_{i}$。
-
计算总距离:总距离为$∑_{i=1}^na_i$。
-
计算每天至少赶路的距离:如果总赶路天数大于0,则每天至少赶路的距离为$\frac{∑_{i=1}n{a_i}}{m−∑_{i=1}nx_i}$。如果总赶路天数小于或等于0,则无法在预定时间内完成所有城市游玩,输出
-1。 -
考虑整数要求:每天赶路的距离必须是整数,因此我们需要向上取整
附:AC代码
#include <bits/stdc++.h> #define int long long using namespace std; const int INF = 2e15, N = 1e5 + 5; int a[n], n, m, l, r = INF; bool check(int x) { int ans = 0; for (int i = 1; i <= n; i++) { ans += ceil(a[i] * 1.0 / x); } return ans <= m; } signed main() { ios::sync_with_stdio(false); scanf("%lld%lld", &n, &m); for (int i = 1, x; i <= n; i++) { scanf("%lld%lld", &a[i], &x); m -= x; } while (l < r) { int mid = l + r >> 1; if (check(mid)) { r = mid; } else { l = mid + 1; } } printf("%lld", l == INF ? -1 : l); return 0; }T2: WTP的大洗牌
题面:
时间限制: 10000ms
空间限制: 1048756kB
题目描述

输入格式

输出格式
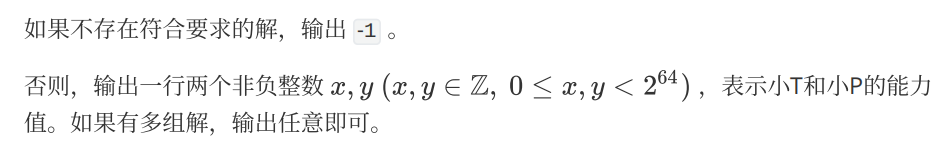
样例
Input 1
3
1 1 1
1 2 3Output 1
10 0
数据范围

做法:
由于前 $10%$,$n=1$
$$
a2+b2=x2+y2
$$直接输出 $a,b$ 即可
由于另外 $20%$,$n=2$
$$
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (a_12+b_12)(a_22+b_22)\
=a_1^2\times a_2^2 +a_1^2\times b_2^2 + b_1^2\times a_2^2 + b_1^2\times b_2^2\
=(a_1b_1)2+(a_2b_1)2+(a_1b_2)2+(a_2b_2)2\
=(a_1b_1)2+2a_1a_2b_1b_2+(a_2b_1)2+(a_1b_2)2-2a_1a_2b_1b_2+(a_2b_2)2\
=(a_1b_1+a_2b_2)2+(a_2b_1-a_1b_2)2$$
直接可以得出答案

附:AC代码
#include <bits/stdc++.h> #define int unsigned long long using namespace std; int n, a[500009], b[500009], m = 1, x = 0, y = 0; signed main() { cin >> n; for (int i = 1; i <= n; i++) cin >> a[i]; for (int i = 1; i <= n; i++) cin >> b[i]; x = a[1], y = b[1]; for (int i = 2, t1, t2; i <= n; i++) { t1 = x, t2 = y; x = t1 * a[i] + t2 * b[i]; y = t1 * b[i] - t2 * a[i]; } cout << x << ' ' << y; }T3:第一题
题面:





样例
Input 1
abyzuv
1Output 1
0
17292
2265252
5092492668516
667116539575596
5552418600567558216Input 2
ctagqkeu
2Output 2
4894148
1324957402927832
7501175624655915608
7097807190249508344做法:
考虑KMP。
唯一需要注意的是这个就是强制在线(
就是一个不能错)。附:AC代码
#include <bits/stdc++.h> #define int unsigned long long using namespace std; const int inf = 1e17; const double eps = 1e-6; const int B = 131; char s[5000005]; int k, kmp[5000005], hash1[5000005], hash2[5000005], ans[5000005], pw[5000005]; signed main() { freopen("easy.in", "r", stdin); freopen("easy.out", "w", stdout); ios::sync_with_stdio(false); cin.tie(NULL), cout.tie(NULL); cin >> s + 1 >> k; int n = strlen(s + 1); pw[1] = B * B, pw[0] = 1; for (int i = 2; i <= n; i++) pw[i] = B * B * pw[i - 1]; int j = 0; for (int i = 1; i <= n; i++) { s[i] = (ans[i - 1] + s[i] - 'a') % 26 + 'a'; if (i != 1) { while (j && s[j + 1] != s[i]) j = kmp[j]; if (s[i] == s[j + 1]) j++; kmp[i] = j; } hash1[i] = hash1[i - 1] * B * B + (s[i] - 'a') * B; hash2[i] = hash2[i - 1] + (s[i] - 'a') * pw[i - 1]; ans[i] = hash1[i] + hash2[i] + ans[j]; } int num = 0; for (int i = 1; i <= n; i++) { num ^= ans[i]; if (!(i % k)) { cout << num << '\n'; num = 0; } } return 0; }T4:WTP的通缉
题面:



样例
Input 1
5 6
4 2 4
2 1 3
4 3 6
2 5 1
1 2 3 4
1 1 2 3
1 1 2 5
2 3 4 5
4 4 5 5
1 2 4 5Output 1
13
13
13
11
5
7做法:

附:AC代码
#include <bits/stdc++.h> #define ll long long #define ls(p) p << 1 #define rs(p) p << 1 | 1 template <typename T> void read(T& x) { x = 0; int flag = 1; char c = getchar(); for (; !isdigit(c); c = getchar()) if (c == '-') flag = -1; for (; isdigit(c); c = getchar()) x = x * 10 + c - '0'; x *= flag; } using namespace std; const int maxn = 100010; int n, q, head[maxn], tot, pa[maxn][20], dep[maxn], lg[maxn]; ll dis[maxn]; struct Edge { int to, nxt, w; } edge[maxn << 1]; struct Node { int l, r; ll sum; } t[maxn << 2], res1, res2; void add(int u, int v, int w) { edge[++tot].to = v, edge[tot].w = w, edge[tot].nxt = head[u], head[u] = tot; } void dfs(int u, int fa) { for (int i = head[u]; i; i = edge[i].nxt) if (edge[i].to != fa) { int v = edge[i].to, w = edge[i].w; pa[v][0] = u, dep[v] = dep[u] + 1, dis[v] = dis[u] + w; dfs(v, u); } } int lca(int u, int v) { if (dep[u] < dep[v]) swap(u, v); int x = dep[u] - dep[v]; while (x) u = pa[u][lg[x & -x]], x -= x & -x; if (u == v) return u; for (int k = min(lg[dep[u]], lg[dep[v]]); k >= 0; k--) if (pa[u][k] != pa[v][k]) u = pa[u][k], v = pa[v][k]; return pa[u][0]; } ll query(int x, int y) { return dis[x] + dis[y] - 2ll * dis[lca(x, y)]; } void push_up(int p) { int a = t[ls(p)].l, b = t[ls(p)].r, c = t[rs(p)].l, d = t[rs(p)].r; t[p] = t[ls(p)].sum > t[rs(p)].sum ? t[ls(p)] : t[rs(p)]; ll w1 = query(a, c), w2 = query(a, d), w3 = query(b, c), w4 = query(b, d); if (w1 > t[p].sum) t[p].sum = w1, t[p].l = a, t[p].r = c; if (w2 > t[p].sum) t[p].sum = w2, t[p].l = a, t[p].r = d; if (w3 > t[p].sum) t[p].sum = w3, t[p].l = b, t[p].r = c; if (w4 > t[p].sum) t[p].sum = w4, t[p].l = b, t[p].r = d; } void build(int p, int l, int r) { if (l == r) { t[p].l = t[p].r = l, t[p].sum = 0; return; } int mid = (l + r) >> 1; build(ls(p), l, mid), build(rs(p), mid + 1, r); push_up(p); } void query(int p, int l, int r, int ql, int qr, Node& res) { if (ql <= l && r <= qr) { if (!res.l) res = t[p]; else { int a = res.l, b = res.r, c = t[p].l, d = t[p].r; if (t[p].sum > res.sum) res = t[p]; ll w1 = query(a, c), w2 = query(a, d), w3 = query(b, c), w4 = query(b, d); if (w1 > res.sum) res.sum = w1, res.l = a, res.r = c; if (w2 > res.sum) res.sum = w2, res.l = a, res.r = d; if (w3 > res.sum) res.sum = w3, res.l = b, res.r = c; if (w4 > res.sum) res.sum = w4, res.l = b, res.r = d; } return; } int mid = (l + r) >> 1; if (ql <= mid) query(ls(p), l, mid, ql, qr, res); if (qr > mid) query(rs(p), mid + 1, r, ql, qr, res); } int main() { read(n), read(q); lg[1] = 0; for (int i = 2; i <= n; i++) lg[i] = lg[i >> 1] + 1; for (int i = 1; i < n; i++) { int u, v, w; read(u), read(v), read(w); add(u, v, w), add(v, u, w); } dfs(1, 0); for (int j = 1; j <= 16; j++) for (int i = 1; i <= n; i++) pa[i][j] = pa[pa[i][j - 1]][j - 1]; build(1, 1, n); while (q--) { int l1, r1, l2, r2; read(l1), read(r1), read(l2), read(r2); res1.l = res1.r = res2.l = res2.r = 0, res1.sum = res2.sum = 0; query(1, 1, n, l1, r1, res1), query(1, 1, n, l2, r2, res2); printf("%lld\n", max(max(query(res1.l, res2.l), query(res1.l, res2.r)), max(query(res1.r, res2.l), query(res1.r, res2.r)))); } return 0; }, lca(a1, b2)), max(lca(b1, a2), lca(b1, b2)))); } return 0; }四、赛后总结
说句闲话,研究OI的最好方法是:
-
成功经验:在第一题中取得满分,显示了我们在某些领域的扎实基础和快速反应能力。这种成功经验值得我们总结和复制。
-
不足之处:在第二、第三和第四题中,我们未能在比赛中得分,这暴露了我们在某些知识点上的薄弱环节。我们需要在未来加强对这些领域的学习和训练。
-
改进措施:为了在未来的比赛中取得更好的成绩,我们需要:
- 加强基础知识的学习,特别是那些在比赛中表现不佳的领域。
- 提高团队的协作能力,确保每个成员都能在团队中发挥最大的作用。
- 增加实战演练,通过模拟比赛来提高我们的应变能力和解题速度。
通过这次比赛,我们不仅看到了自己的不足,也发现了潜力。我们相信,通过不断的努力和学习,我们能够在未来的挑战中取得更好的成绩。让我们以这次比赛为契机,继续前进,不断超越自我。
附:随笔
OI之路:勇往直前
一、自我反思与成长
在这次比赛中,我深刻地认识到了自己的不足,并明确了未来的训练目标。这不仅是一次自我检验的机会,更是一次自我提升的契机。正如李白所言:“乘风破浪会有时,直挂云帆济沧海”,在茫茫人海中,我们虽然弱小,但也要勇敢地面对挑战,展现出“苔花如米小,也学牡丹开”的精神。
二、努力的价值与意义
通过这次比赛,我也看到了自己努力的成果。这不仅给予了我继续在OI之路上披荆斩棘的勇气与动力,更让我明白,每一次的努力都是向成功更进一步。正如“轻肌弱骨散幽葩,更将金蕊泛流霞”,即使我们的力量微小,也要有不断向上的决心和勇气。
三、高处的风景与挑战
“仁者见仁,智者见智”,成为优秀的人,看到的世界是不一样的。每当你登上一座新的山峰,都会享受那里细腻清风的洗涤,与明媚阳光的沐浴。与其在山脚说山顶是令人心驰神往的,不如立刻付诸行动。高处的风景虽然美丽,但也需要我们不断地努力和攀登。
四、保持谦逊与虚心
余秋雨在《文化苦旅》中说道,“繁华转眼凋零,喧嚣是短命的别名”。我们不能在拥有一点知识后就自我满意,“水满则溢,月满则亏,自满则败,自矜则愚”。我们要保持虚心的心态与视角,不耻下问,同时,向高处攀登。
五、持续的努力与奔跑
一个跑者,在一场马拉松中,是不会停下的,因为一旦停下,就很难再重新跑起来。在一眼望不到边的OI赛道上,我们或快,或慢,或前,或后,但这些都不重要。从现在起,不要停下,一直跑下去吧。
六、结语
综上所述,努力吧,OIer!“可不要辜负自己的努力啊,2024还有机会在等着我呢!”让我们以这次比赛为契机,继续前进,不断超越自我。
“可不要辜负自己的努力啊,2024还有机会在等着我呢!” ——Syx
-