前言
因为本人天资愚钝,所以总喜欢将抽象化的事务具象化表达。对于各类眼花缭乱的树,只需要认知到它们只是一种数据结构,类似数组,切片,列表,映射等这些耳熟能详的词汇。对于一个数据结构而言,无非就是增删改查而已,既然各类树也是数据结构,它们就不能逃离增删改查的桎梏。
那么,为什么我们需要树这种数据结构呢,直接用数组不行吗,用切片不行吗?当然可以,只不过现实世界是缤纷杂乱的,而又没有一种万能药式的数据结构以应对千变万化的业务需求。所以,才会有各类树,而且一些“高级”数据结构是基于树形数据结构的,例如映射。
二叉树
在中文语境中,节点结点傻傻分不清楚,故后文以 node 代表 "结点",root node 代表根节点,child node 代表 “子节点”
二叉树是诸多树状结构的始祖,至于为什么不是三叉树,四叉树,或许是因为计算机只能数到二吧,哈哈,开个玩笑。二叉树很简单,每个 node 最多存在两个 child node,第一个节点称之为 root node。
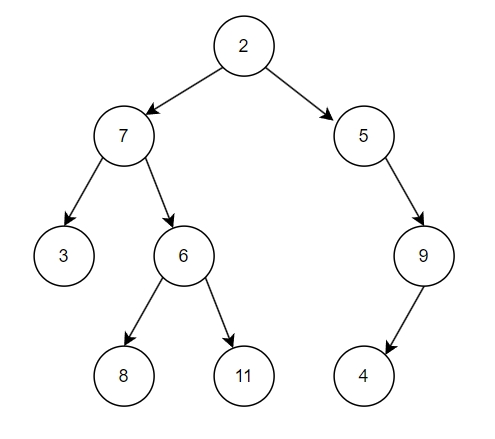
二叉树具备着一些基本的数学性质,不过很简单,定义从 i 从 0 开始:
- 第
i层至多有2i个 node; - 深度为 i 层二叉树至多有
2i+1-1个 node。
二叉树的特殊类型
这里有兴趣的可以了解一下,不影响后文的阅读。二叉树根据 child node 的不同,衍生出了几种特殊类型:在一颗二叉树中,如果每个 node 都有 0 或 2 个 child node,则二叉树是满二叉树;定义从 i 从 0 开始,一棵深度为 i,且仅有 2i+1−1 个 node 的二叉树,称为完美二叉树;若除最后一层外的其余层都是满的,并且最后一层要么是满的,要么在右边缺少连续若干 node,则此二叉树为完全二叉树。
二叉搜索树
二叉搜索树(Binary Search Tree),也叫二叉查找树,有序二叉树,排序二叉树(名字还挺多)。它是一种常用且特殊的二叉树,它具备一个特有的性质,left node(左结点)始终小于 parent node (父结点),right node 始终大于 parent node。
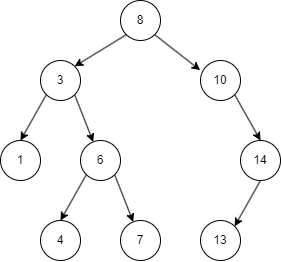
二叉搜索树的查找
- 二叉搜索树从 root node 开始,如果命中则返回;
- 否则,目标值比 node 小进入 left node;
- 比 node 大进入 right node;
- 如果左右都为空,则未命中。
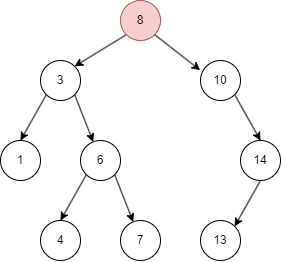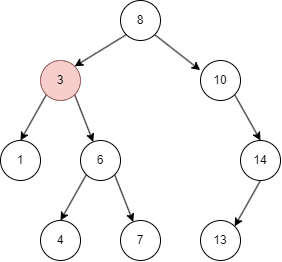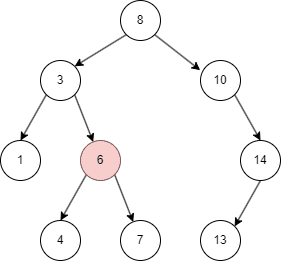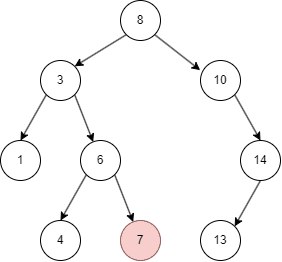
二叉搜索树的遍历
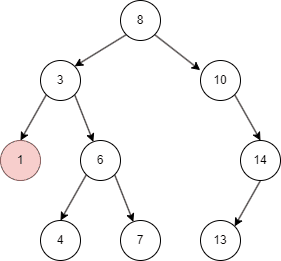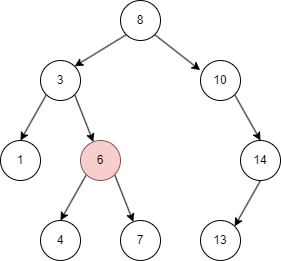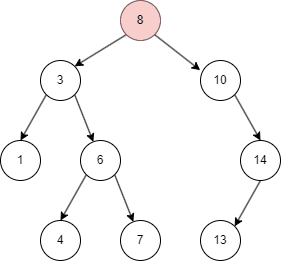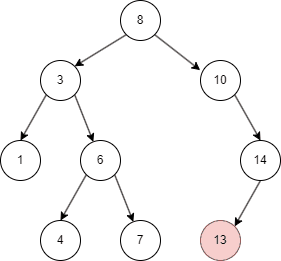
二叉搜索树有不同的遍历方式,这里介绍常用的中序遍历方式:
- 先遍历左子树;
- 然后查找当前左子树的 parent node;
- 遍历右子树。
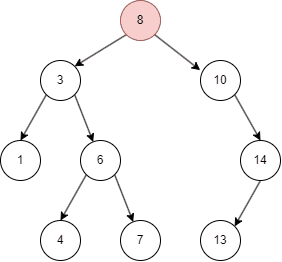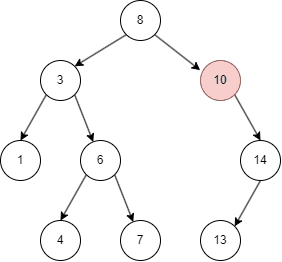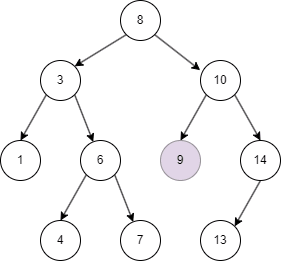
二叉搜索树的插入
- 二叉搜索树从 root node 开始,如果命中则不进行操作;
- 否则,目标值比 node 小进入 left node;
- 比 node 大进入 right node;
- 最终将值插入搜索停止的地方。
二叉搜索树的删除
二叉树的删除和查询基本一致,只要在命中时删除即可。
- 二叉搜索树从 root node 开始,如果命中则删除;
- 否则,目标值比 node 小进入 left node;
- 比 node 大进入 right node;
- 删除后使用该 node 左子树最大值或者右子树最小值替代该 node。
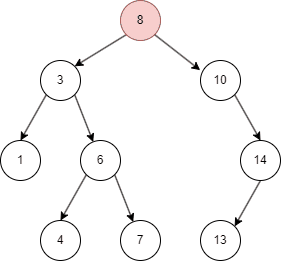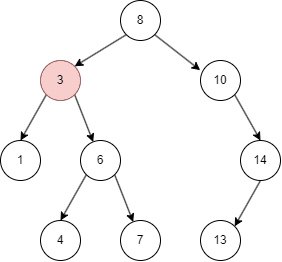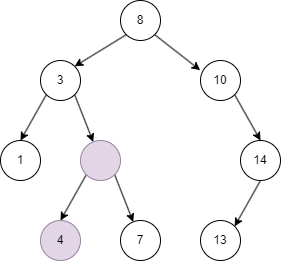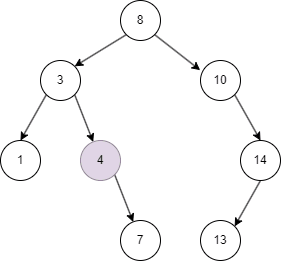
自平衡二叉树
从上面的几张动图中我们知晓,二叉搜索树不同于线性结构,它可以大大降低查找,插入的时间复杂度。但在特殊情况下,二叉搜索树可能退化为线性结构,假如我们依次插入1,2,3,4,5:

此时,二叉搜索树退化为线性结构,效率重新变回遍历。于是,便出现了自平衡二叉树,例如 AVL 树,红黑树,替罪羊树等。但它们并不是本文重点,下面我要介绍的是另外一种很常见的自平衡二叉树:B树。
B树
B树和B-树是同一个概念。B树相对于二叉树有两点最大的不同:
- 每个 node 可以有不止一个数值
- 每个 node 也可以有不止两个 child node
B树有两种类型 node:
- internal node(内部结点):不仅仅存储数据,也具备 child node;
- leaf node(叶子结点):仅存储数据,不具备 child node。
这两种 node 不同于前文所提的 root node 和 child node。root 和 child 是相对于阶层的概念,而 internal 和 leaf 是相对于性质的概念
一个简单的图例如下:
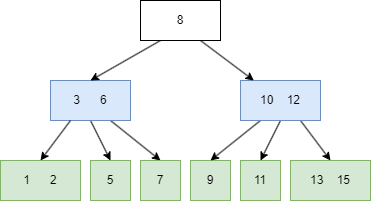
图中的蓝色方块是 internal node,绿色则是 leaf node。
B树有一些需要满足的性质,这里的抽象的逻辑有些烧脑,我会对照前面的图片来解释。设定一颗 m 阶的B树,m = 3:
设 internal node 的 child node 个数为 k:
- 如果 internal node 是 root node,那么
k = [2, m],比如上图的 8 有两个 child node(3|6, 10/12); - 如果 internal node 不是 root node,那么
k = [m/2, m],m/2 向上取整,比如上图的3|6有三个 child node; - 如果 root node 的
k为 0,那么 root node 是 leaf 类型的; - 所有 leaf node 在同一层,上图最后一行的六个 node。
设任意 node 键值个数为 n:
- 对于 internal node,
n = k-1, 升序排序,满足k[i] < k[i+1],比如上图的三个 internal(8,3|6,10|12) 都满足此规律; - 对于 leaf node,
n = [0, m-1],同样升序排序,比如上图最后一个的六个 leaf,其键值最多为两个。
上述的概念有些抽象,但是这是理解B树关键的地方所在,后面在B树的插入讲解,会有更多具象的动图来解释这些概念。
B树的查找
B树的查找类似于二叉树:
- 从 root node 开始,如果目标值小于 root node,进入左子树,否则进入右子树;
- 遍历 child node 的多个键值;
- 如果匹配到键值,则返回;
- 如果不匹配,则根据目标值的范围选择对应的子树;
- 重复步骤2、3、4,直到匹配成功返回或者未找到。
假如我们要查找 11:
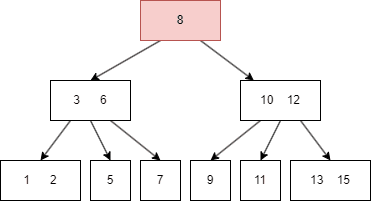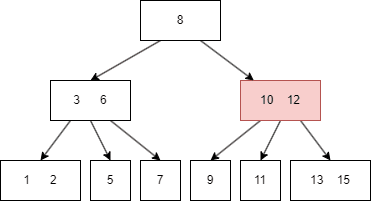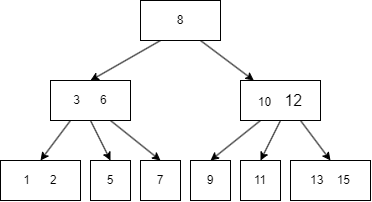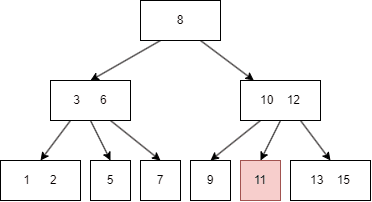
B树的遍历
B树的遍历方式类似二叉搜索树,不过因为B树一个 node 有多个键值和多个 child node,所以需要遍历每个左右子树和键值:
- 先遍历第一个左子树,也就是 parent node 第一个键值的左边;
- 然后查找当前 parent node 的第一个键值;
- 遍历第二个左子树,也就是 parent node 第二个键值的左边;
- 遍历完搜索的左子树,最后遍历当前 parent 的最右子树,即最后一个键值的右边。
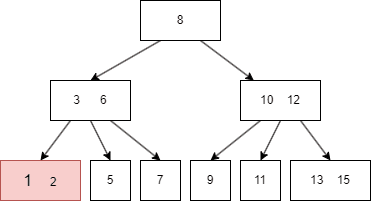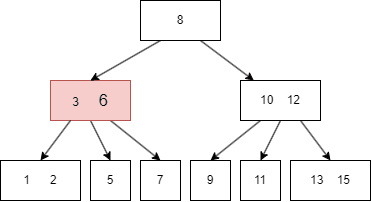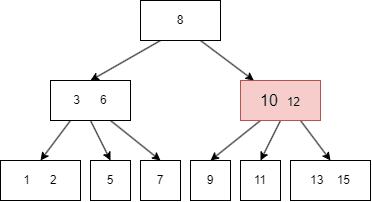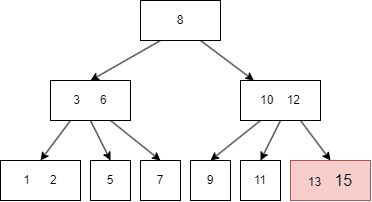
B树的插入
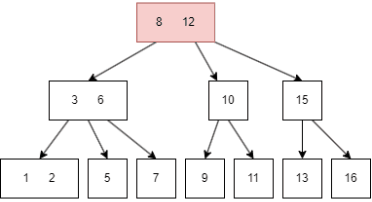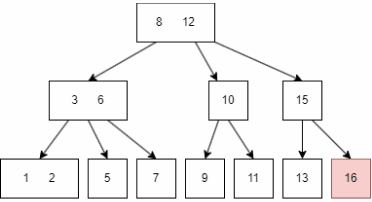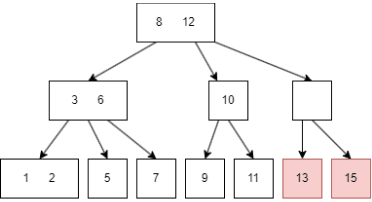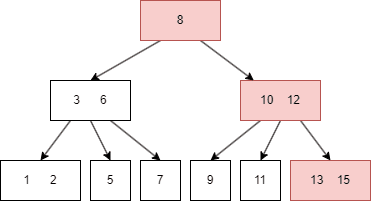
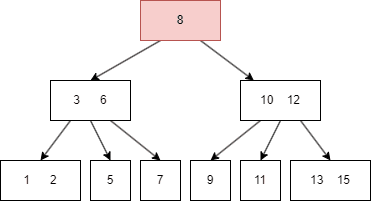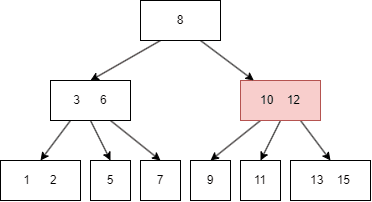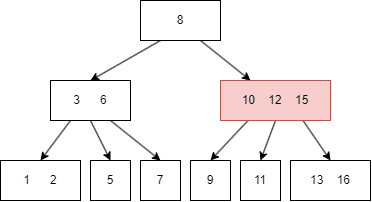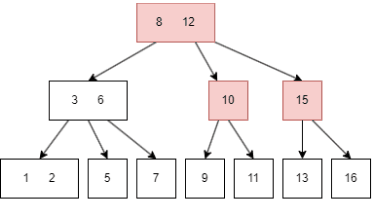
插入前面的过程和查询一致,在插入后可能需要重整 node,以符合B树的性质,例如插入 16:
- 先查找到目标 node,也就是
13|15; - 因为这是一颗 3 阶B树,所以 node 最多只能有两个键值,于是向上传递中间值 15;
- parent node 最多也只能有两个键值,于是继续向上传递中间值 12;
- 此时 root node 是 8|12,需要有三个 child node,于是 10|15 需要拆分,再向下进一步调整,至此,插入 16 完成。
B树的删除
删除是插入的逆操作,但是往往比插入更复杂,因为删除后经常需要重整 node:
- 先查找到目标 node,也就是
16; - 删除 16,此时 15 child node 剩下一个,不符合条件,递归向上调整,一直到根节点;
- 直到所有的条件都满足后,删除 16 完成。