807. 保持城市天际线
问题描述
给你一座由 n x n 个街区组成的城市,每个街区都包含一座立方体建筑。给你一个下标从 0 开始的 n x n 整数矩阵 grid ,其中 grid[r][c] 表示坐落于 r 行 c 列的建筑物的 高度 。
城市的 天际线 是从远处观察城市时,所有建筑物形成的外部轮廓。从东、南、西、北四个主要方向观测到的 天际线 可能不同。
我们被允许为 任意数量的建筑物 的高度增加 任意增量(不同建筑物的增量可能不同)。 高度为 0 的建筑物的高度也可以增加。然而,增加的建筑物高度 不能影响 从任何主要方向观察城市得到的 天际线 。
在 不改变 从任何主要方向观测到的城市 天际线 的前提下,返回建筑物可以增加的 最大高度增量总和 。
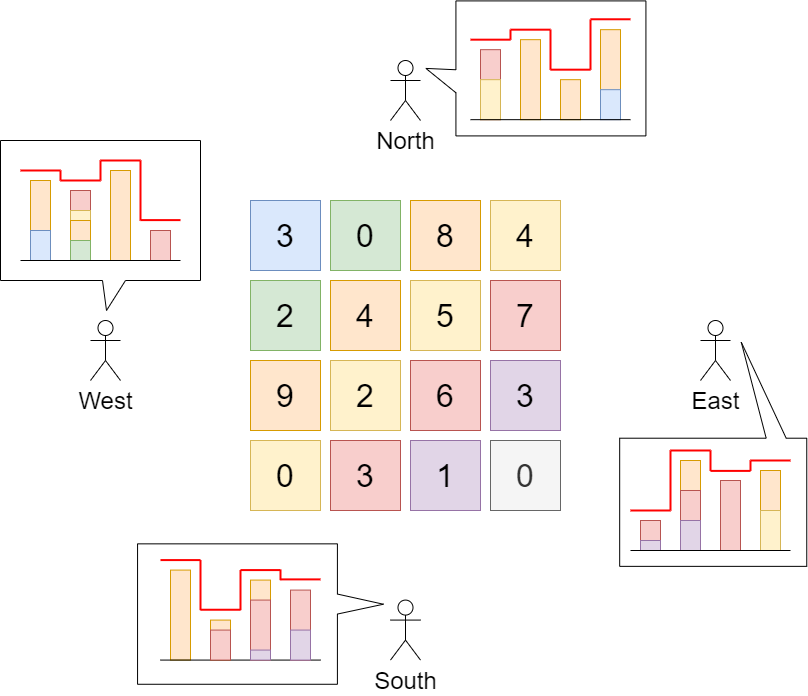
输入:grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
输出:35
解释:建筑物的高度如上图中心所示。
用红色绘制从不同方向观看得到的天际线。
在不影响天际线的情况下,增加建筑物的高度:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]
思路
我们可以想到 North 和 South , West 和 East 方向看到的天际线应该是相同的高度,相反的顺序(从左至右、从右至左)。对于 grid 数组中的任意一个元素 grid[i][j] 其增量取决于第 i 行和第 j 列中的两个最大值中的最小值。
例如考虑 grid[0][0],第 0 行的最大值为 8,第 0 列的最大值为 9,其余值不影响天际线的高度,因此我们只需要考虑在增加了增量后不超过这两个天际线的高度(不产生视图的变化)。那么我们就可以得到一个贪心的逻辑:
-
维护两个行列数组,记录对应行/列中的最大值。
-
把 grid 数组中的元素其两个数组中对应的行列进行比较,选择两值中较小的值作为天际线的位置,增量的值就是天际线的位置减去 grid 数组中当前元素的高度。
代码实现
class Solution {
public:
int maxIncreaseKeepingSkyline(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> maxRaw(m, 0);
vector<int> maxCol(n, 0);
for (int raw = 0; raw < m; raw++) {
for (int col = 0; col < n; col++) {
/** 记录竖向遍历中,每一行的最大值, raw 是不变量 */
maxRaw[raw] = max(maxRaw[raw], grid[raw][col]);
/** 记录横向遍历中,每一列的最大值,col 是变量 */
maxCol[col] = max(maxCol[col], grid[raw][col]);
}
}
int result = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
result += min(maxRaw[i], maxCol[j]) - grid[i][j];
}
}
return result;
}
};
切蛋糕的最小总开销
题目描述
有一个 m x n 大小的矩形蛋糕,需要切成 1 x 1 的小块。
给你整数 m ,n 和两个数组:
-
horizontalCut 的大小为 m - 1 ,其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
-
verticalCut 的大小为 n - 1 ,其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。
一次操作中,你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一:
-
沿着水平线 i 切开蛋糕,开销为
horizontalCut[i]。 -
沿着垂直线 j 切开蛋糕,开销为
verticalCut[j]。
每次操作后,这块蛋糕都被切成两个独立的小蛋糕。
每次操作的开销都为最开始对应切割线的开销,并且不会改变。
请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。
思路
首先,每条水平线和垂直线,最终都要全部切完。
-
水平线(横切)开销 horizontalCut[i] 对答案的贡献,等于
horizontalCut[i]乘以在此之前竖切的次数加一。 -
垂直线(竖切)开销 verticalCut[j] 对答案的贡献,等于
verticalCut[j]乘以在此之前横切的次数加一。
对于一个操作序列,交换其中两个相邻的横切,不影响答案;交换其中两个相邻的竖切,也不影响答案。所以重点考察交换两个相邻的横切和竖切。
设横切的开销为 h,在此之前竖切的次数加一为 cntV;设竖切的开销为 v,在此之前横切的次数加一为 cntH。
-
先横切,再竖切,开销为
h⋅cntV+v⋅(cntH+1); -
先竖切,再横切,开销为
v⋅cntH+h⋅(cntV+1)。
如果先横再竖开销更小,则有
h⋅cntV+v⋅(cntH+1) < v⋅cntH+h⋅(cntV+1)
化简得:h>v
这意味着,谁的开销更大,就先切谁,并且操作顺序与 cntH 和 cntV 无关。按照该规则去切蛋糕,得到的操作序列,如果把开销大的操作移动后面,必然会得到更大的总开销。
代码实现
class Solution {
public:
long long minimumCost(int m, int n, vector<int>& horizontalCut, vector<int>& verticalCut) {
sort(horizontalCut.begin(), horizontalCut.end(), greater<int>());
sort(verticalCut.begin(), verticalCut.end(), greater<int>());
long long cost = 0;
int rowIndex = 0, colIndex = 0;
/** 横切和竖切的刀数*/
int rowCnt = 1, colCnt = 1;
while (rowIndex < m - 1 && colIndex < n - 1) {
/** 贪心——>选择代价最大的切法能够减少开销 */
if (horizontalCut[rowIndex] > verticalCut[colIndex]) {
/** cost = Σ(cost/cut * cnt) */
cost += horizontalCut[rowIndex++] * rowCnt;
colCnt++;
} else {
cost += verticalCut[colIndex++] * colCnt;
rowCnt++;
}
}
/** 结束最小开销计算,现在计算总开销 */
for (int i = rowIndex; i < m - 1; i++) {
cost += horizontalCut[i] * rowCnt;
}
for (int j = colIndex; j < n - 1; j++) {
cost += verticalCut[j] * colCnt;
}
return cost;
}
};
总结
今天主要学习了贪心算法的二维运算逻辑,不论是天际线问题还是切蛋糕问题,都需要很好的理解行 row 和列 col 之间的关系,遍历的顺序和逻辑对结果的影响非常大。