01字典树
01字典树是一种只有0和1两种边的字典树。可以解决查询第 \(k\) 小,查询 \(x\) 是第几小等问题。
查询第 \(k\) 小
可以把输入的数转成等长二进制,然后插入01字典树。比如将 \([0,0,1,3,3]\) 插入字典树:
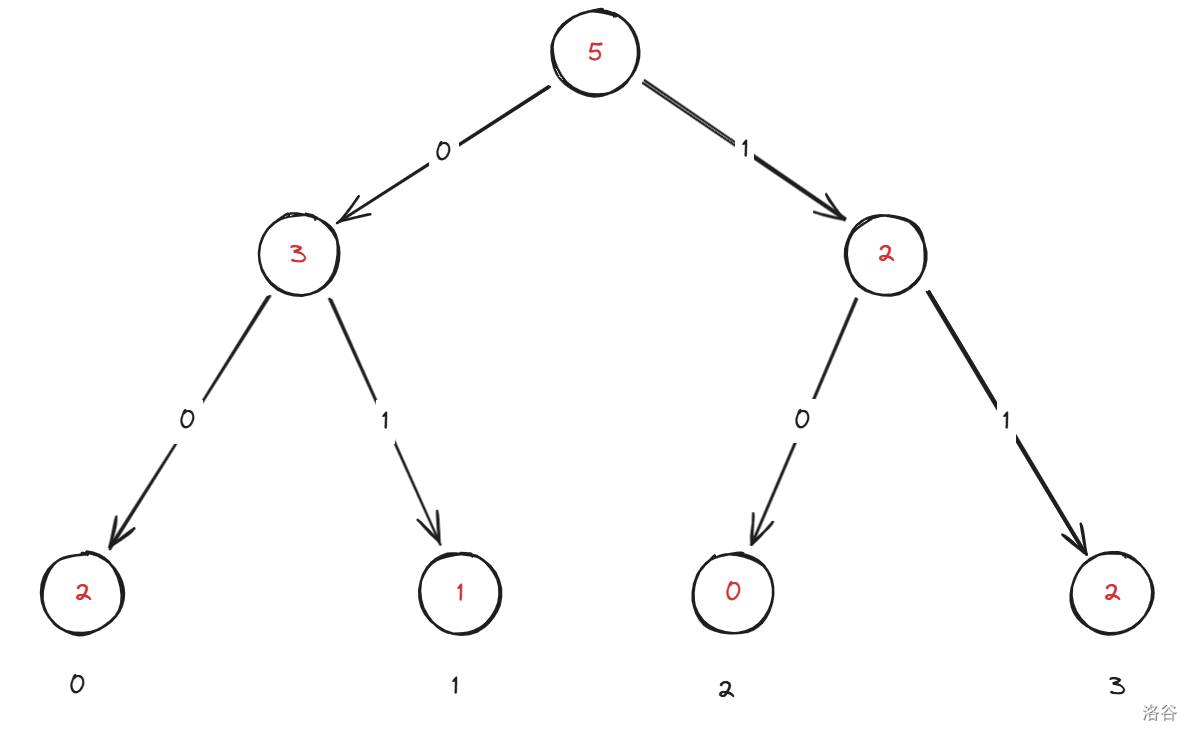
这里红色数字表示以该段为前缀的数的个数,黑色表示对应的数。
假设我们要查询第 \(3\) 小,可以发现根节点的左子树里有 \(3\) 个数,即第 \(3\) 小在左子树内:
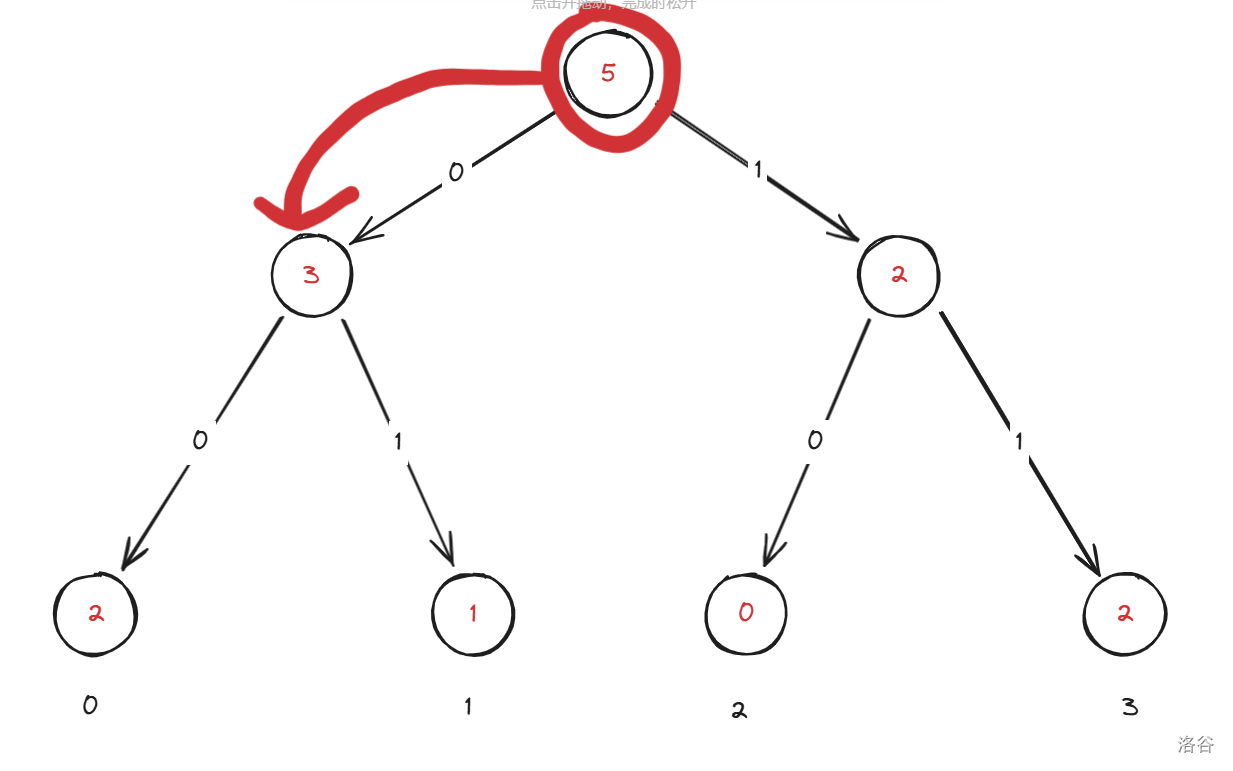
接着看,左子树内只有两个数,说明答案在右子树内:
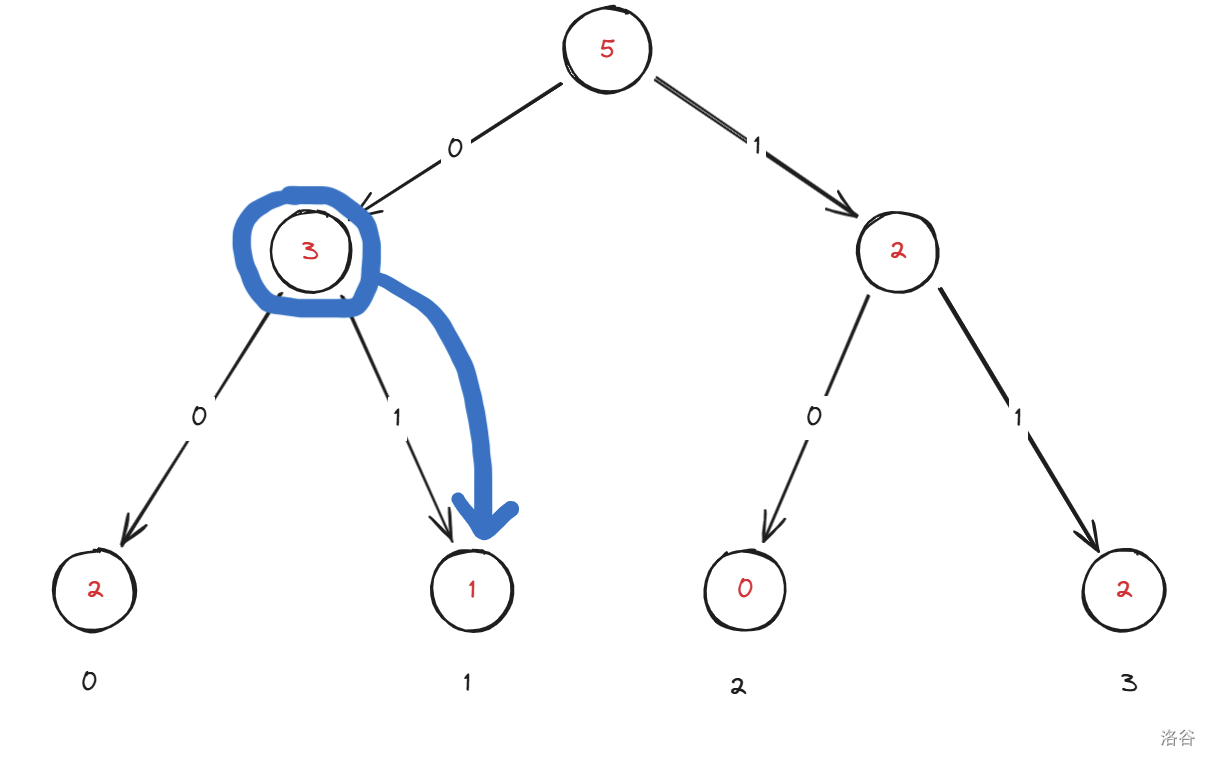
最终我们就得到了答案 \(1\)。
观察这个过程,可以发现第 \(k\) 小的求法:
- 当左子树内的数的个数 \(cnt< k\),则答案在右子树内,\(k\leftarrow k-cnt\)。
- 否则答案在左子树内。
不断递归上述过程,直到找到答案。
空间复杂度 \(O(N \log \max \{a_i\})\),单次查询时间复杂度 \(O(\log \max \{a_i\})\)。
代码
int GetNum(int k) {
int u = 1, ans = 0;
for(int i = 29; i >= 0; --i) {
if(cnt[son[u][0]] < k) {
k -= cnt[son[u][0]], u = son[u][1], ans = (ans << 1) | 1;
}else {
u = son[u][0], ans <<= 1;
}
}
return ans;
}
GetNum(k);
查询 \(x\) 为第几小
这个很容易明白,就不多做解释了。
重复执行以下过程:
- 如果 \(x\) 在右子树,则 \(ans \leftarrow ans+cnt\),其中 \(ans,cnt\) 分别为答案和左子树的数的数量。
- 否则什么也不做。
- 走到对应的儿子上。
最终的答案就为 \(ans+1\)。
空间复杂度 \(O(N \log \max \{a_i\})\),单次查询时间复杂度 \(O(\log \max \{a_i\})\)。
代码
int GetRnk(int x) {
int u = 1, ans = 1;
for(int i = 29; i >= 0; --i) {
if((x >> i) & 1) {
ans += cnt[son[u][0]], u = son[u][1];
}else {
u = son[u][0];
}
}
return ans;
}
GetRnk(x);
\(x\) 与其中一数的最大异或和
贪心地考虑即可:
- 如果当前这位存在与 \(x\) 的不同的,则选择这一位
- 否则不选择
空间复杂度 \(O(N \log \max \{a_i\})\),单次查询时间复杂度 \(O(\log \max \{a_i\})\)。
代码
int GetMaxXor(int x) {
int u = 1, ans = 0;
for(int i = 29; i >= 0; --i) {
if(cnt[son[u][!((x >> i) & 1)]) {
u = son[u][!((x >> i) & 1)], ans = (ans << 1) | 1;
}else {
u = son[u][(x >> i) & 1], ans <<= 1;
}
}
return ans;
}
GetMaxXor(x);
01字典树还有很多用处,这里就不多说了。
可持久化01字典树
可持久化01字典树和01字典树只有一个区别,它可以查询任意时刻的01字典树。
首先,我们能想到的最暴力的方法就是每次修改都复制一颗字典树。虽然这样很明显空间会爆掉,但我们还是先看看。比如在 \([0,0,1,3,3]\) 中再加入一个 \(2\):
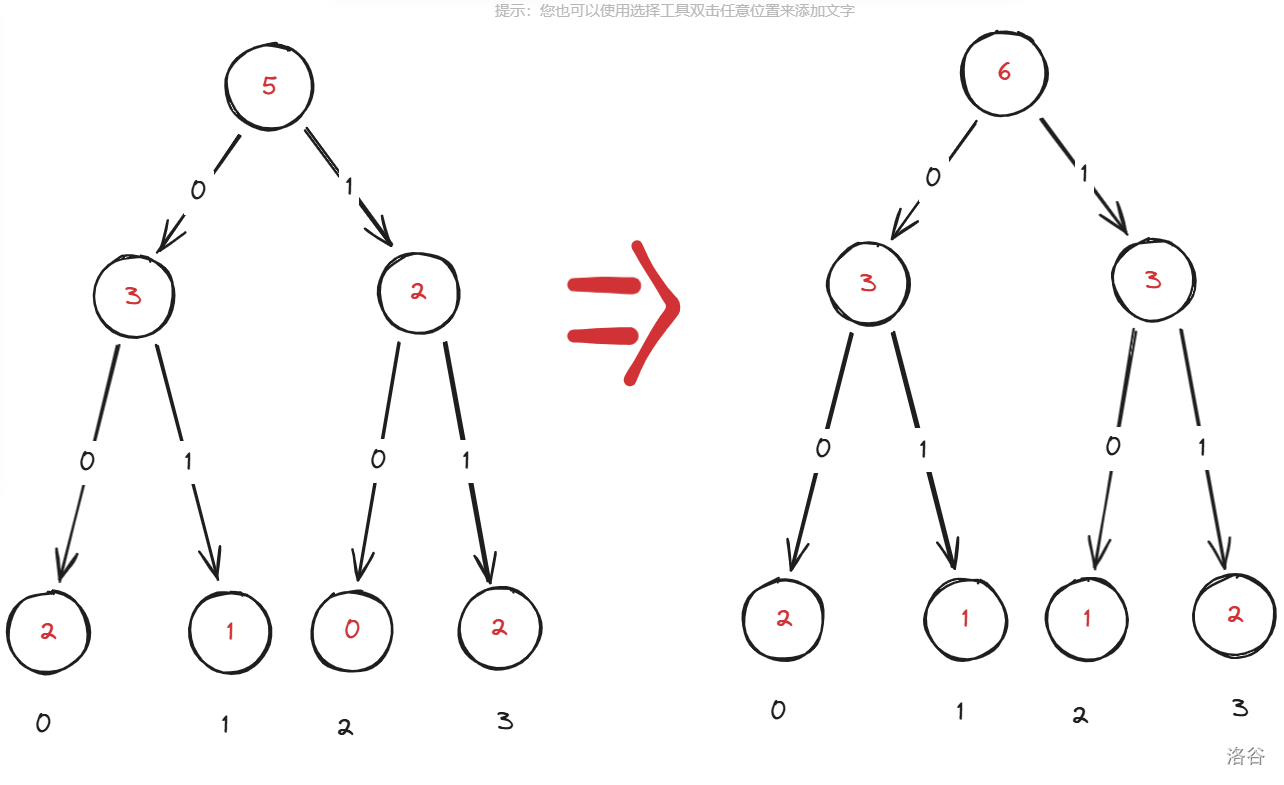
你可能会注意到,其中大部分的点都没有变化,只有处于 \(2\) 的这条链上有变化,我们不妨这么做:
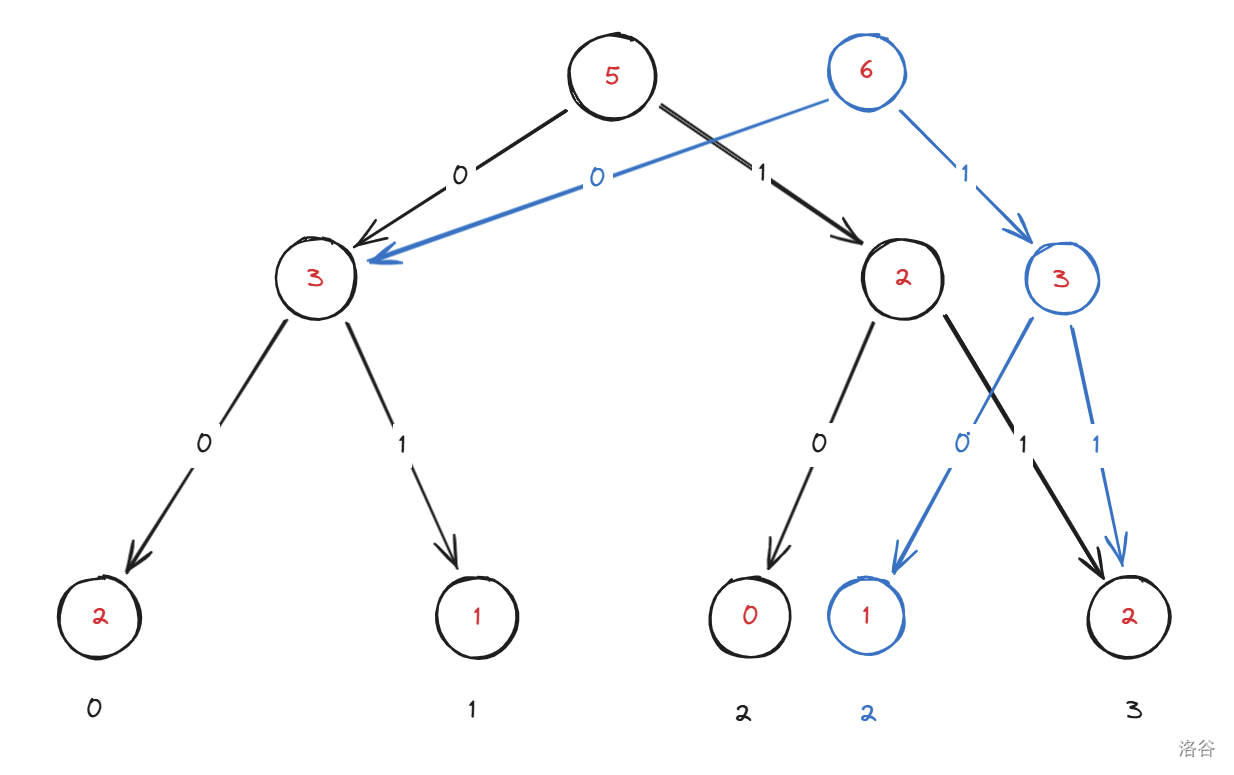
可以发现现在总共只加入了 \(O(\log \max \{a_i\})\) 个点!
而可持久化字典树也正是这样运作的,就是把不用修改的子树直接指向之前的。在查找历史版本时直接从对应的根节点搜下去就行了。
空间复杂度 \(O((N+M) \log \max \{a_i\})\),单次插入时间复杂度 \(O(\log \max \{a_i\})\)。
代码
void Insert(int x, int id, int pos, int val) {
ROOT[id] = ++tot;
int u = tot, v = ROOT[x];
for(int i = 19; i >= 0; --i) {
son[u][(pos >> i) & 1] = ++tot;
son[u][!((pos >> i) & 1)] = son[v][!((pos >> i) & 1)];
u = son[u][(pos >> i) & 1], v = son[v][(pos >> i) & 1];
}
cnt[u] = val;
}
Insert(x, y, pos, val);
查询区间第 \(k\) 小
01字典树只能求全体第 \(k\) 小,但无法求区间第 \(k\) 小。而区间第 \(k\) 小也很简单,即两个前缀字典树相减再查询。
空间复杂度 \(O((N+M) \log \max \{a_i\})\),单次查询时间复杂度 \(O(\log \max \{a_i\})\)。
代码
int GetNum(int l, int r, int k) {
int u = ROOT[r], v = ROOT[l - 1], ans = 0;
for(int i = 29; i >= 0; --i) {
if(cnt[son[u][0]] - cnt[son[v][0]] < k) {
k -= cnt[son[u][0]] - cnt[son[v][0]], u = son[u][1], v = son[v][1], ans = (ans << 1) | 1;
}else {
u = son[u][0], v = son[v][0], ans <<= 1;
}
}
return ans;
}
GetNum(l, r, k);
查询 \(x\) 是区间第几小
两个前缀字典树相减再查询即可。
空间复杂度 \(O((N+M) \log \max \{a_i\})\),单次查询时间复杂度 \(O(\log \max \{a_i\})\)。
代码
int GetRnk(int l, int r, int x) {
int u = ROOT[r], v = ROOT[l - 1], ans = 1;
for(int i = 29; i >= 0; --i) {
if((x >> i) & 1) {
ans += cnt[son[u][0]] - cnt[son[v][0]], u = son[u][1], v = son[v][1];
}else {
u = son[u][0], v = son[v][0];
}
}
return ans;
}
GetRnk(l, r, x);