最短路径问题
最短路问题是图论中一种重要的算法,本章将包括:
目录一.概念
1.概念
一张图中n条点和m条边,边都有权值,权值可正可负。边可能有向,可能无向,给定起点s和终点t,在所有能链接s和t的路径中,寻找所经权值最小的路径,此为最短路径问题。
2.解决方案
最容易想到的方法是暴力法,枚举所有路径,再进行大小比较,但明显不可行,一定会超时。
更好的方法即为在寻路的过程中,动态规划将要走的最短路径,此也为下文的算法思路和方法。
二. \(Flord\) 算法
\(Flord\) 算法是最简单的最短路径算法,甚至短于暴力搜索。
1.算法思想
求 \(i\) 到 \(j\) 的最短路径,对于其他所有点,每个点 \(k\) 都尝试一遍能否 \(i\) 借道 \(k\) 到 \(j\) 会不会更短。
对于这样的思路,我们可以用动态规划来解决,定义 \(dp[k][i][j]\) ,表示 \(k\) 阶段 \(i\) 到 \(j\) 的最短路,不难发现 \(dp[k][i][j]\) 是由 \(dp[k-1][i][j]\) 推出,1.若不变,则直接继承。2.若变,则是其加借道的权值即可。由是,我们便可推出其状态转移方程:
\[dp[k][i][j]=min(dp[k-1][i][j],dp[k-1][i][k]+dp[k-1][k][j]) \]由状态转移方程可知, \(dp[k][i][j]\) 的值只与 \(dp[k-1][i][j]\) 有关,由是,我们可利用滚动数组将 \(dp\) 数组降维,来到二维,得到新的状态转移方程:
\[dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]) \]综上,可得出 \(Flord\) 算法的核心代码。
2.代码详解
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
}
}
由于使用了滚动数组,所以 \(k\) 循环必须在 \(i\) , \(j\) 循环之外。
3.算法应用及局限性
对于 \(Flord\) 算法来说,其能一次跑出所有点对之间的最短路,我们称这种求所有点对之间的最短路的问题为多源最短路问题,对比其他算法来说,解决多源最短路问题, \(Flord\) 算法 \(O(n^3)\) 的均摊复杂度是最优秀的。
当然,对于求一组点对之间的最短路的单源最短路问题, \(Flord\) 算法 \(O(n^3)\) 的复杂度便难以接受。
综上, \(Flord\) 算法适合解决 \((n<300)\) 的小图上的最短路问题。
二. \(Djikstra\) 算法
\(Djikstra\) 算法基于 \(BFS\) 可以说“ \(Djikstra\) = \(BFS\) +贪心”
1.算法思想
对于 \(Djikstra\) 算法来说,主要为点之间的扩展,对于我们将要处理的点来说,我们将其所有邻居加入优先队列中。再在优先队列中选择最小(队首的)的那条边进行处理,优先队列中存放的是各点到起点的距离。
经过手动模拟,可以得出,若一个点 \(A\) 在之前的处理中已确定到起点的最小值,则后续的处理与其无关,即对于一个点,若其已被确定,则其不会再入队。
2.代码详解
void dijkstra(int s){ //s为起点
for(int i=1;i<=n;i++){dis[i]=inf;done[i]=false;}
//初始化,dis[i]表示i点到起点的距离,done[i]表示i点已确定。
dis[s]=0; //起点到自己的距离为0
priority<node>q; //优先队列,小根堆
q.push(node(s,0));
while(!q.empty()){
node u=q.top(); //弹出距离最小的点
q.pop();
if(done[u.id]) continue; //若此点已确定
done[u.id]=true;
for(int i=0;i<=e[u.id].size();i++){
edge y=e[u.id][i];
if(done[u.to]) continue;
if(dis[v.to]>y.w+u.dis){ //若通过此点更短
dis[y.to]=y.w+u.dis;
q.push(node(y.to,dis[y.to]));
}
}
}
}
3.算法特征及其局限性
\(Djikstra\) 算法是较为高效,稳定的最短路径算法,每次得出一条最短路径,所以稳定,每次只更新一个点,所以高效。
当然, \(Djikstra\) 算法也并非完美无缺,其也有其局限性,那就是对于其将要处理的图来说,其不能出现权值为负的情况,若有负边权,则贪心不成立,即不能保证“全局最优解由局部最优解组成”的最优性定理,导致 \(Djikstra\) 算法出现错误。
三. \(Bellman-ford\) 算法
\(Bellman-ford\) 算法是一种简单的单元最短路算法。
1.算法思路
我们通过多次推出,来松弛(指修改到各点的最短距离)各点的最短距离,也就是说通过一步步地推出最远的点的最近路径。
对于我们进行的每一次松弛来说,对每一条线段进行遍历,看线段端点经过此线段能否比之前距起点的距离更近,若是,则更新。由于考虑回退边的存在,所以共进行 \(n\) 次操作。
2.代码详解
\(Bellman-ford\) 算法的主代码较少:
for(int k=1;k<=n;k++)
for(int i=1;i<=m;i++)
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i]
注:保证在主代码之前初始化 \(dis\) 数组,除 \(dis[s]\) 之外,全部初始化为 \(INF\) 。
3.算法特性
由算法思路得, \(Bellman-ford\) 算法遍历 \(n\) 条边 \(m\) 条边,其复杂度为 \(O(mn)\) ,虽然其能处理 \(Djikstra\) 处理不了的负边权问题,但当 \(n\) 与 \(m\) 都很大时, \(Bellman-ford\) 算法的效率将会十分糟糕,不过这也引出了我们的的第四种算法 \(SPFA\) 。
四. \(SPFA\) 算法
\(SPFA\) 算法基于 \(Bellman-ford\) 算法的队列优化版。
1.算法思想
既然其是 \(Bellman-ford\) 算法的优化,那么基本的思想不会改变,我们需要找到如何优化 \(Bellman-ford\) ,对于 \(Bellman-ford\) 的每一次松弛来说,我们需要遍历每一条边,其实并没有必要,对于一个其邻居已经确定的点来说,重复遍历它的每条边是无意义的,我们只需对发生变化的点的邻居进行维护即可,队列完全适合,于是这便是 \(SPFA\) 算法。
2.代码详解
bool inq[maxn]; //inq[i]表示i已在队列中
void spfa(int s){ //s为起点
for(int i=1;i<=n;i++){dis[i]=inf;inq[i]=false;} //dis[i]为i到起点的距离
dis[s]=0;
queue<int>q;
q.push(s);
inq[s]=true;
while(!q.empty()){
int u=q.front();
q.pop();
inq[u]=false;
for(int i=0;i<e[u].size();i++){
int v=e[u][i].to,w=e[u][i].w;
if(dis[u]+w<dis[v]){
dis[v]=dis[u]+w;
if(!inq[v]){ //若v不在队列中
inq[v]=true;
q.push(v); //入队
}
}
}
}
}
3.特征及性质
\(SPFA\) 算法节点的入队数量决定了 \(SPFA\) 算法的效率,由于不能确定重新入队的节点数量,所以 \(SPFA\) 不稳定,最差情况下为 \(O(mn)\) ,此时我们便应选择稳定的 \(Djikstra\) 算法来解决问题。
当给定的图如下图时:
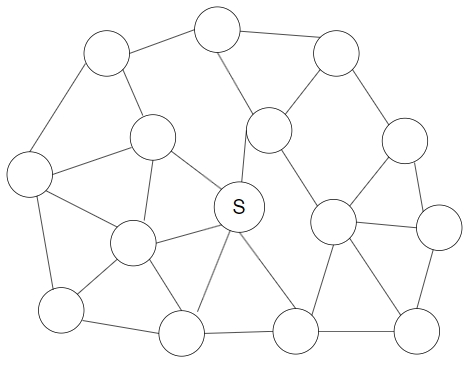
\(SPFA\) 的复杂度将十分糟糕,不如 \(Djikstra\) 。当然, \(SPFA\) 也有自己的优点,即允许负边权的存在。其也可用来判断负环。
五.总结
这四种算法各有千秋。
| 问题 | 边权 | 算法 | 复杂度 |
|---|---|---|---|
| 非负数 | \(Djikstra\) | \(O((m+n)log_2n)\) | |
| 单源最短路 | 允许有负数 | \(Bellman-ford\) | \(<O(mn)\) |
| 允许有负数 | \(SPFA\) | \(O(mn)\) | |
| 多远最短路 | 允许有负数 | \(Flord\) | \(O(n^3)\) |
其中,求多源最短路,则使用 \(Flord\) ,若求单源最短路且无负边权,则推荐使用稳定的 \(Djikstra\) 。若有负边权,则使用 \(SPFA\) ,\(Bellman-ford\) 的应用场景很少,一般不会用到,可用来做小图的小码量选择。
标签:路径,SPFA,Bellman,最短,问题,算法,Djikstra,ford,dp From: https://www.cnblogs.com/adsd45666/p/18263462