题意
给定一张 \(n \times m\) 的地图。
对于第 \(0\) 列,第 \(m + 1\) 列,第 \(0\) 行,第 \(n + 1\) 行,有 \(2n + 2m\) 个人,每个人面朝地图中心。
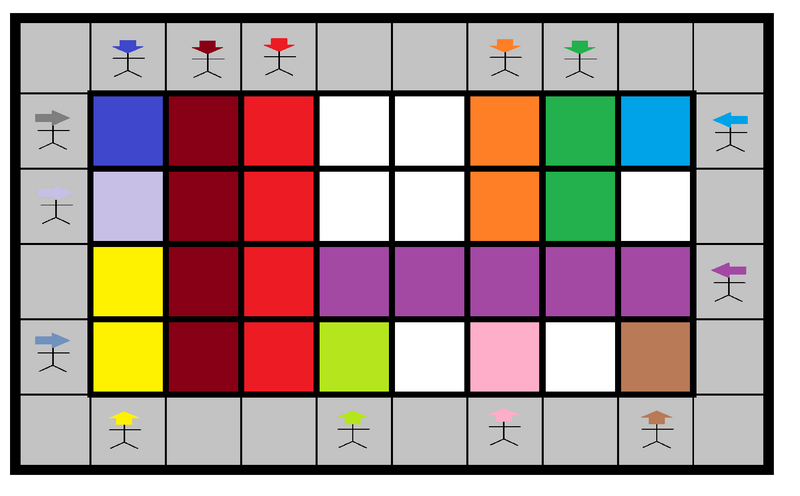
每个人走到别人染过色的位置,或走出地图,将走过的地方染色。
你需要求出共有多少种本质不同的染色方案。
\(n, m \le 10 ^ 6\)
Sol
直接做似乎很不好做,考虑一些特殊情况。
一个人都没有输出 \(1\)。
若只有两个方向,且两个方向对立,显然答案为 \(2\) 的次幂。
若只有两个方向的人且两个方向相邻,显然答案为 \(\dbinom{x + y}{x}\)。
考虑有三个方向的时候。
假设目前的三个方向分别为:向右,向下,向上,分别设人数为 \(x, y, z\)。
若当前有一列被贯通,那么右边部分变为两个方向且对立的情况。
考虑枚举第一列被贯通的位置。
那么显然对于左边的部分,一定有至少有一行被染满。
枚举当前最后一个染满的行 \(i\),则又变为两个子问题。
对于上方的是无限制,显然答案为 \(\dbinom{i + y - 1}{i - 1}\)。
对于下方不能被染满行,考虑这个东西的组合意义,那么很显然就是不能到达最后一列。
所以答案为 \(\dbinom{x - i + z}{x - i - 1}\)。
合起来:
\[\begin{aligned} & \sum_{i = 1} ^ {x} \dbinom{i + y - 1}{i - 1} \dbinom{x - i + z}{x - i - 1} \\ & = \sum_{i = 0} ^ {x - 1} \dbinom{i + y}{i} \dbinom{x - i + z - 1}{x - i - 1} \\ &= \dbinom{x + y + z - 1}{x - 1} \end{aligned} \]这样就搞完了。
考虑四个方向的,不难发现必定有一列或一行贯穿,可以只考虑一列的情况,而一行可以翻转得到。
枚举最后一列被染满的,右边部分就是标准的三方向问题,直接组合数搞完了,左边部分可以染满一列,设 \(f_i\) 表示前 \(i\) 列的方案数。
若当前一列染满,直接就是 \(f_{i - 1}\),而没染满就是说明前面没有任何一列染满,也是三方向问题。
最后考虑一下上下是否都有 \(1\),若都有 \(1\),当前答案与 \(f_i\) 都要 \(\times 2\)。
Code
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <array>
#define int long long
using namespace std;
#ifdef ONLINE_JUDGE
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
char buf[1 << 23], *p1 = buf, *p2 = buf, ubuf[1 << 23], *u = ubuf;
#endif
int read() {
int p = 0, flg = 1;
char c = getchar();
while (c < '0' || c > '9') {
if (c == '-') flg = -1;
c = getchar();
}
while (c >= '0' && c <= '9') {
p = p * 10 + c - '0';
c = getchar();
}
return p * flg;
}
string read_() {
string ans;
char c = getchar();
while (c != '0' && c != '1')
c = getchar();
while (c == '0' || c == '1')
ans += c, c = getchar();
return ans;
}
void write(int x) {
if (x < 0) {
x = -x;
putchar('-');
}
if (x > 9) {
write(x / 10);
}
putchar(x % 10 + '0');
}
bool _stmer;
const int N = 1e6 + 5, M = 4e6 + 5, mod = 998244353;
int pow_(int x, int k, int p) {
int ans = 1;
while (k) {
if (k & 1) ans = ans * x % p;
x = x * x % p;
k >>= 1;
}
return ans;
}
array <int, M> fac, inv;
void init(int n) {
fac[0] = 1;
for (int i = 1; i <= n; i++)
fac[i] = fac[i - 1] * i % mod;
inv[n] = pow_(fac[n], mod - 2, mod);
for (int i = n; i; i--)
inv[i - 1] = inv[i] * i % mod;
}
int C(int n, int m) {
if (n < m || n < 0 || m < 0) return 0;
return fac[n] * inv[m] % mod * inv[n - m] % mod;
}
int Y(int x, int y, int z) {
if (!x) return (!y && !z);
return C(x + y + z - 1, x - 1);
}
void Mod(int &x) {
if (x >= mod) x -= mod;
if (x < 0) x += mod;
}
bool _edmer;
signed main() {
cerr << (&_stmer - &_edmer) / 1024.0 / 1024.0 << "MB\n";
init(4e6);
/* while (1) { */
/* int x = read(), y = read(), z = read(); */
/* write(Y(x, y, z)), puts(""); */
/* } */
int n = read(), m = read();
string sL = " " + read_(), sR = " " + read_(), sU = " " + read_(), sD = " " + read_();
int tp1 = 0, tp2 = 0, tp3 = 0, tp4 = 0;
for (int i = 1; i <= n; i++) tp1 += sL[i] == '1';
for (int i = 1; i <= n; i++) tp2 += sR[i] == '1';
for (int i = 1; i <= m; i++) tp3 += sU[i] == '1';
for (int i = 1; i <= m; i++) tp4 += sD[i] == '1';
int len = (tp1 && 1) + (tp2 && 1) + (tp3 && 1) + (tp4 && 1);
if (len <= 1) return puts("1"), 0;
if (len == 2) {
if ((tp1 + tp2) && (tp3 + tp4))
return write(C(tp1 + tp2 + tp3 + tp4, tp1 + tp2)), puts(""), 0;
int res = 1;
for (int i = 1; i <= n; i++)
if (sL[i] == '1' && sR[i] == '1')
res = res * 2ll % mod;
for (int i = 1; i <= m; i++)
if (sU[i] == '1' && sD[i] == '1')
res = res * 2ll % mod;
return write(res), puts(""), 0;
}
auto solve = [&](string tL, string tU, string tD, int _tp2, int _tp3, int _tp4) -> int {
int ans = 0, sum = 0;
int l1 = 0, l2 = 0, l3 = 0; //Left Up Down
for (int i = 1; i <= n; i++) l1 += tL[i] == '1';
for (int i = 1; i <= m; i++) {
if (tU[i] == '0' && tD[i] == '0') continue;
int tp0 = (tU[i] == '1' && tD[i] == '1') ? 2 : 1;
sum += Y(l1, l2, l3), Mod(sum);
sum = sum * tp0 % mod;
if (tU[i] == '1') l2++;
if (tD[i] == '1') l3++;
ans += sum * Y(_tp2, _tp3 - l2, _tp4 - l3) % mod, Mod(ans);
}
return ans;
};
/* cerr << solve() << "@@" << endl, exit(0); */
int ans = 0;
ans += solve(sL, sU, sD, tp2, tp3, tp4), Mod(ans);
swap(n, m);
ans += solve(sU, sR, sL, tp4, tp2, tp1), Mod(ans);
write(ans), puts("");
return 0;
}