筛选能带的方法
在重复23年science论文时，使用了ratio和ratio2，就是判断局域在板附近的程度
注意还要筛选Q因子：if(ewfd.Qfactor>1e6,1,0)
不用整个BZ都扫描，这样太慢了
就扫两个点
求带隙
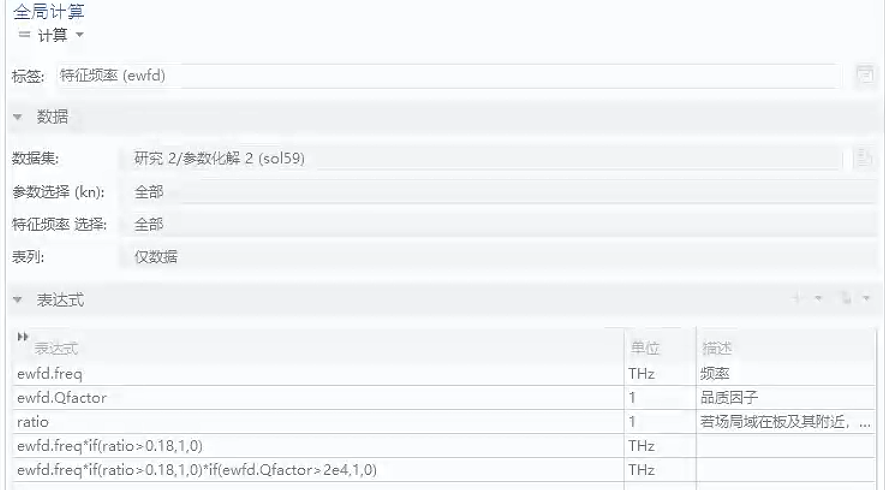
在派生值-计算中，可以计算一些表达式的表格！辅助筛选，精确知道一些点的值，很有用！
注意这样设置：
从二维到三维，摸索能带的方法：
以Lieb晶格这个为例。
目前已经知道二维的能带、模场、f与r/a的关系：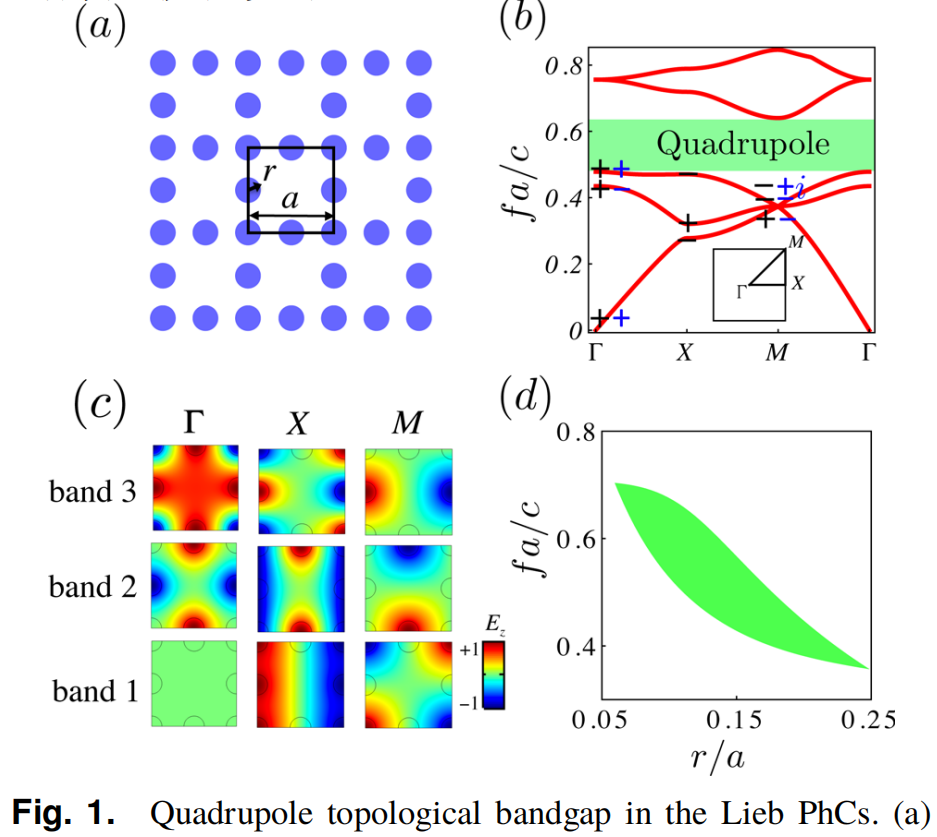
当周期a设为700nm时，二维情况的能带：二维情况：柱板：TM模式：a=700nm，r=0.12aimage ibe (Hz)3.5|2.5]Ls!osWEOC- a6SR: BE Hed Be二oo 9606600086060660...[1]
三维情况仿真步骤
先从频率最低的一条能带仿真起【即对应于二维情况的最低的一条能带】，而不要随便设成0-1000Hz范围，然后特征频率数设为50，这样算出来得到的能带我发现只会显示400-600THz的能带，低于400和高于600THz的能带不会显示，而且我没发现400-600THz的能带与二维情况的能带[1:1]有什么相似的地方。
先仔细观察二维情况时的能带图[2]，知，要计算带隙的话，只需要计算Gamma点和M点就可以。另外，要特别注意这种简并点和高对称点，在M点有一个三重简并点，它们的模场画在c图中。所以在计算三维的能带图时，由于三维板周期结构的计算量太大，就只需要计算两个点Gamma点和M点就可以！另外，参数化扫描的方法是：使用"手动"，然后就在二维的带隙附近搜索就可以了，所需特征频率数设为40！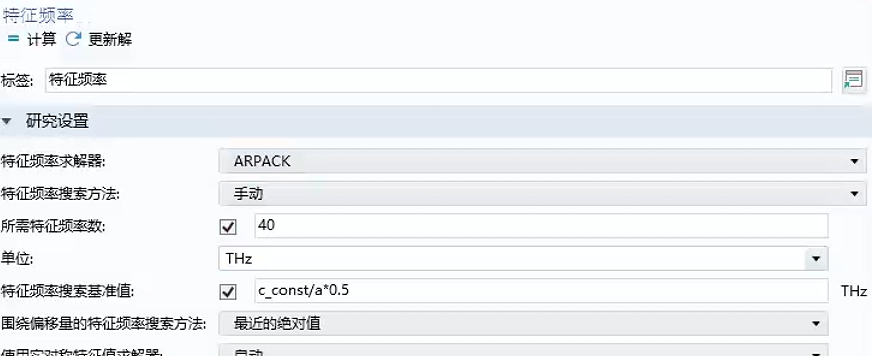 
，另外，对于这种三维周期结构，又不是计算有限结构，在构建网格时，不能直接"物理场控制网格-来自研究" 
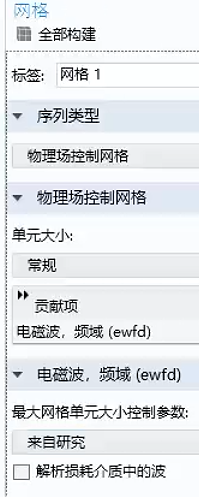【虽然张师兄是这样做，但是这样是不对的，虽然算出来能带大概是对的，但是相位是算不准确的，还是要物理场控制网格-用户定义中设置a/8！ 】，
算完后，寻找Gamma点的三重简并点对应的频率，寻找方法就是：先用局域程度ratio和Q因子进行筛选，筛选后再寻找三重简并的频率点【注意此时由于是个板，可能不像二维一样完美的三重简并，而是三个特别特别接近的频率】，找到后看看这三个点对应的模场，是否会对应二维情况的模场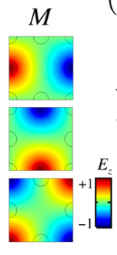
【这是来自c图，它就是三重简并点处的三个模场】，如果对应的话，那么就可以确定这个频率点对应二维能带图M点中的那个三重简并点。
而对于Gamma点，在ratio和Q因子筛选后，通过模场一个一个与二维情况时导带Gamma点模场进行比较，从三重简并点的频率上下多少，可以得到三维情况时，Gamma点的导带底对应于二维情况时导带底的频率。
首先，根据光子晶体书109页对光子晶体板厚的说法，对柱板，厚度d_thickness取为2*a=1400nm，此时计算结果为：
注意通过综合筛选Q因子和局域比例ratio，可以得到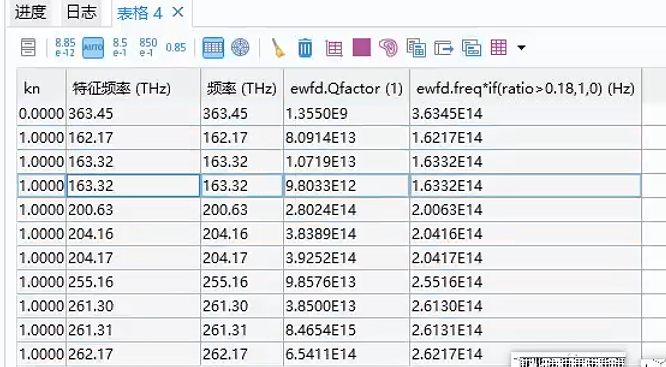
，利用方法[3]，可以知道
确实是三重简并点，且惊奇地发现，此时三维柱板的三重简并点的频率竟然和二维情况的三重简并点的频率[1:2]几乎一样，都是160THz附近，z切面的模场也相同。另外，在163THz，
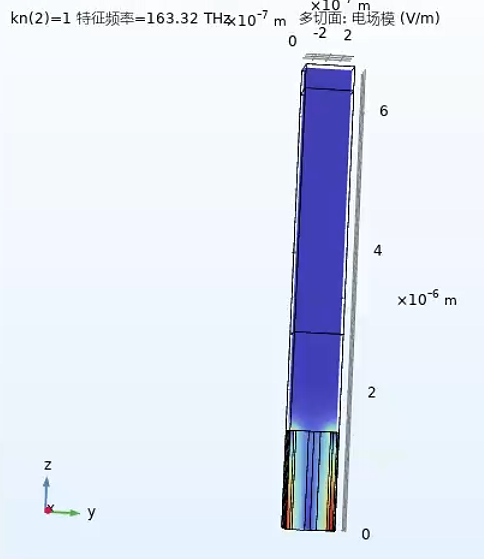，z方向没有节点，是基模。而当到163的下一个频率【是200THz】，其z方向切面：
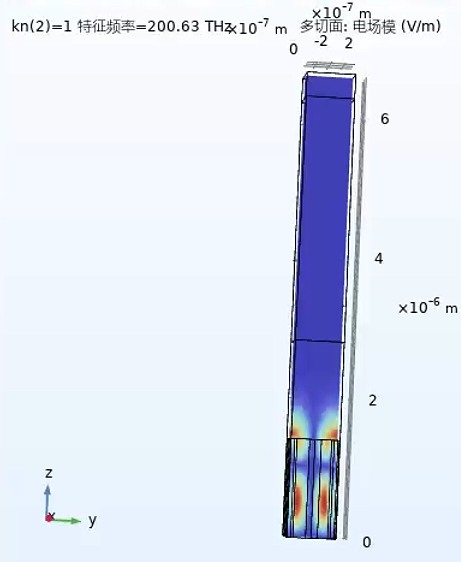，可以发现有一个节点，它是高阶模。然而，200THz这个频率并不会高于Gamma点的最高价带的频率、且也不对应于二维情况M点的最低导带的频率（大概275THz）：
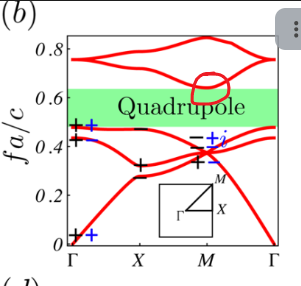。所以200THz这个点是额外出现的高阶模式，见注意在光子晶体书108页其实说了：image 8.2 ”极化和板厚为什么选择的柱板比孔板厚(将近四倍)? 这与极化有着密切的关系。图3 是柱板和孔板带隙尺寸与板厚的关系, 确实存在一个最佳厚度...[4]，它出现的原因是，由于板太厚，z方向就像一个波导了，也会存在模式。
注意在光子晶体书108页其实说了：
，这里垂直节点指的就是z方向有节点，那么就是高阶模式。
三维光子晶体板的模式、能带 会与二维情况有一些对应相同!
厚度越厚，三维板的情况会越来越接近二维情况的能带【因为二维情况就是厚度为无穷】
寻找三维情况特征频率的规律：
崔师弟说：从二维情况到三维情况，特征频率大概是从二维情况的特征频率变换到1.5~2倍。这是因为在二维情况，相当于z方向无限长，而在三维情况，z方向有限。相当于变薄了，则有效折射率变小【因为相当于有一些体积变成了空气，而空气的折射率更小】，所以特征频率变大。【有效折射率越小，频率变大的原因可以见光子晶体书，注意介质带和空气带，空气带频率更高，而空气的介电常数小】
另外，其实有效折射率还会和模式有关，因为不同模式频率不同
三维周期结构的情况，特征频率与周期a、板厚、hole或柱的占空比 之间的关系：
当unit cell周期a增大时，能带、特征频率会下降。
原因：粗略理解是：a相当于波长，a增大，波长增加，特征频率下降。我也仔细计算过：在下面尝试更改r/a=0.18，a=700nm，二维，TE[5] 和 当参数为a=350nm,r1=0.18a时，二维情况时的TE能带：[6] 情况对比，可以知道，当a越小，特征频率会增加。
在光子晶体书18页也说了这个问题：
，就是整体缩放。
当a变为原来的两倍（即整体放大为两倍），则频率变为原来的1/2！
当周期a增大时，光锥高度会下降，
这个可以通过a=350nm时的光锥：image 7000.51.52.5 [7]和a=700nm时的光锥：image 350300250-500.5 1 1.52.5 [8] 对比知道，注意光锥只和a有关。
特征频率与板厚之间的关系
崔师弟说：从二维情况到三维情况，特征频率大概是从二维情况的特征频率变换到1.5~2倍。这是因为在二维情况，相当于z方向无限长，而在三维情况，z方向有限。相当于变薄了，则有效折射率变小【因为相当...[9]
板厚度越小，特征频率越大
特征频率f与占空比r/a的关系
目前已经知道二维的能带、模场、f与r/a的关系：image 0.25一=eeeeeee 一(三ee e eee eeSeegeree ee下妆上eeeeeee3 2 1/ 一人3 C Ms)...[2:1] 中的d图
从此图可以知道，当a不变时，当r增大，频率都减小，带隙也变化
特别注意，光子晶体书18页说：尺寸扩大为多少倍，频率就缩小为多少分之一。
特别注意，如果光子晶体均匀地缩放为原来的 s倍，对应的带隙宽度将变成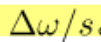 
。因此， 与晶体尺度无关的 更有用的表征手段是带隙宽度与带隙中心频率的比值。
综上，由于厚度为2a=1400nm时存在高阶模式，所以要把板厚减小，当板厚400nm时：
注意仿真目标是要把Lieb晶格的TM带隙移动到200THz-300THz这个区域：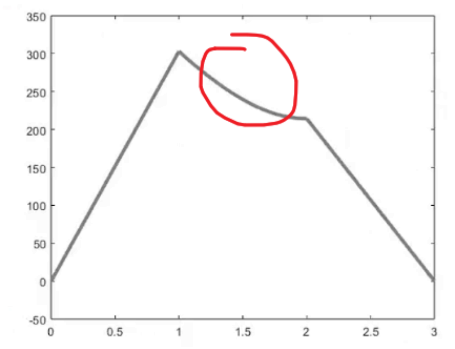
。
当板厚400nm时：M点处三重简并点位于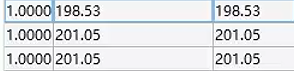
这三个频率。
然后这个三重简并点之上的另一个频率为283.22THz，通过看其z方向垂直切面，发现其没有垂直节点，然后再将z切面的模场与二维时的模场对比，知道这个点就对应于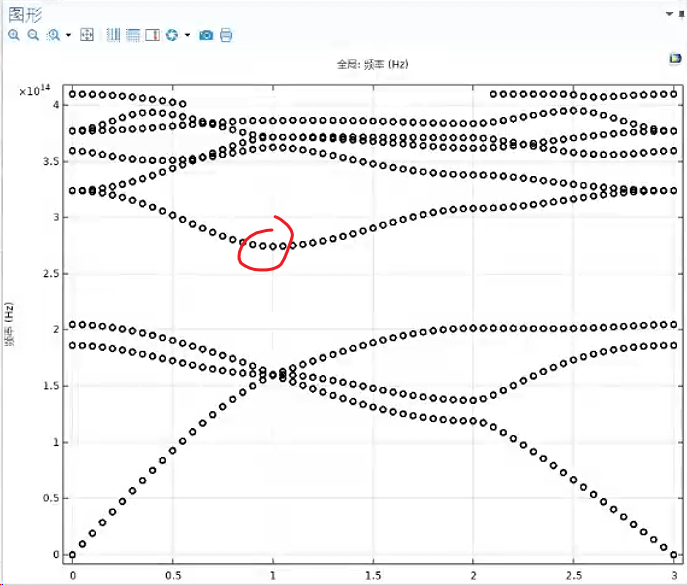
！
导带频率有点太接近300THz，
由于二维情况，在超胞以及旋转以后，带隙是这样：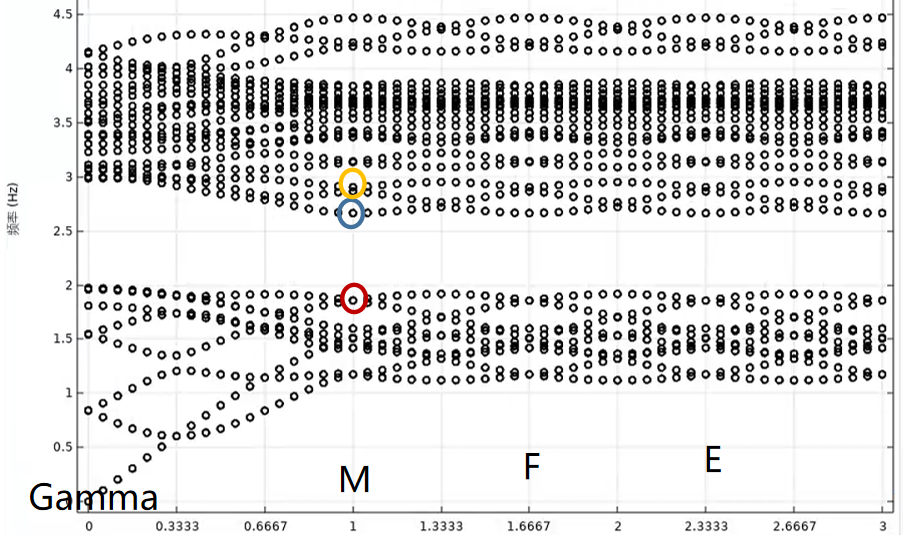
所以400nm的情况适合研究价带
但导带在什么情况适合研究？
500厚度时，导带底降低到280，降的太少，只降低了3THz，还是要改r
根据特征频率f与占空比r/a的关系[10]，大致判断r/a需要为0.125、0.3、0.14，进行参数化扫描
目前已经知道二维的能带、模场、f与r/a的关系：image 0.25一=eeeeeee 一(三ee e eee eeSeeger... ↩︎ ↩︎
先仔细观察二维情况时的能带图，知，要计算带隙的话，只需要计算Gamma点和M点就可以。另外，要特别注意这种简并点和高对称点，在M... ↩︎
注意在光子晶体书108页其实说了：image 8.2 ”极化和板厚为什么选择的柱板比孔板厚(将近四倍)? 这与极化有着密切的关系... ↩︎
下面尝试更改r/a=0.18，a=700nm，二维，TE
我从0.12a改成0.18a，
能带依然很不一样，但可以看到有一个带隙好像在逐渐打开
↩︎
当参数为a=350nm,r1=0.18a时，二维情况时的TE能带：
在450THz附近有带隙，大概是14THz的带隙，此带隙与23science论文的带隙差不多，所以估计可以。不过450THz若在三维情况，确实在光锥之内，因为光锥是和周期a有关，画光锥的代码为：
%% 绘制lightline % 由于光锥，而根据comsol中kn和kx的关系，在这段，kx=. % 然后带入omega=kx*c，就可以得到光锥的omega与kn的关系 figure4=figure(4); kn_array1 = 0:1/100:1; kn_array2 = 1:1/100:2; kn_array3 = 2:1/100:3; c_light = 3e8; %光速 a_comsol = 350e-9; %来自comsol中的a f_lightline1 = c_light*sqrt((pi/a_comsol*kn_array1).^2+(pi/a_comsol*kn_array1).^2)./(2*pi*1e12); f_lightline2 = c_light*sqrt((pi/a_comsol).^2+(-pi/a_comsol*kn_array2+2*pi/a_comsol).^2)./(2*pi*1e12); f_lightline3 = c_light*(-pi/a_comsol*kn_array3+3*pi/(a_comsol))./(2*pi*1e12); %这是一个行向量,注意单位是THz 另外，特别注意还要除以2pi,因为光锥线是f=c*k/(2pi)！！！ plot(kn_array1(1,:),f_lightline1(1,:),'color',[127/255 127/255 127/255],'LineWidth',3); hold on; plot(kn_array2(1,:),f_lightline2(1,:),'color',[127/255 127/255 127/255],'LineWidth',3); hold on; plot(kn_array3(1,:),f_lightline3(1,:),'color',[127/255 127/255 127/255],'LineWidth',3);a=350nm时的光锥：
↩︎
a=350nm时的光锥：
↩︎a=700nm时的光锥：
↩︎崔师弟说：从二维情况到三维情况，特征频率大概是从二维情况的特征频率变换到1.5~2倍。这是因为在二维情况，相当于z方向无限长，而... ↩︎
特征频率f与占空比r/a的关系
↩︎
