回来补补题。
分析:
我先考虑 \(k\) 很大的时候,大块和大块间的移动,我们不得不尽量避免小块:
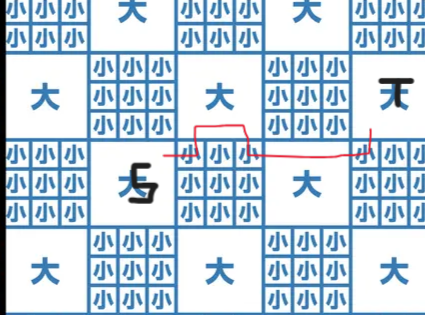
我们容易发现这样时是最优的,可以发现就是在斜着走,也就是典型的切比雪夫距离。斜着走一次需要经过两条边,所以花费是两倍的切比雪夫距离。
要是起点和终点不在大块上呢?
首先考虑它们不在同一大块(这里的大块意义不同于前面说的大块,具体见下)内:
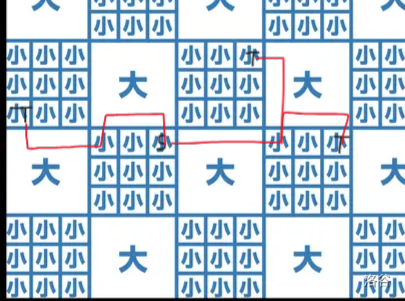
显然,路径上必然是从起点到一个相邻的大块,然后进行大块和大块间的移动到达与终点相邻的大块,然后再直直进入。
路径简化为:起点 到 起点相邻的大块 再到 终点相邻的大块 最后到 终点。
我们明确起点和终点,但起点相邻的大块和终点相邻的大块并不确定,但相邻的大块只有 \(4\) 个,所以枚举一下 \(4\times 4\) 就行了,如果起点或终点本来就在大块上就不用考虑了。
要是它们是在同一大块的小块呢?
如图:
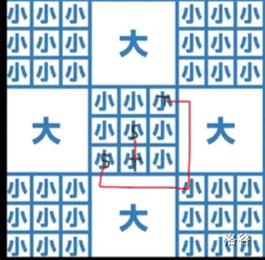
那么它们间的路径可能就不会经过大块了,可以在小块内之间相互抵达,但也可能经过大块,所以还是要进行上面的那种讨论。
\(k\) 较小时呢?
\(k=1\),显然就不用考虑那么多了,直接就是曼哈顿距离了。
\(k=2\) 呢?
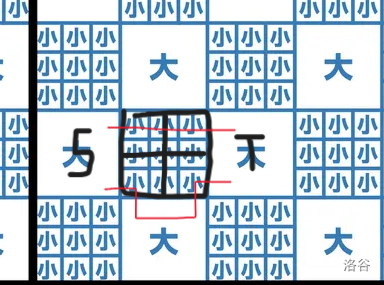
大块间移动的最短距离不再是切比雪夫距离了,特判一下就行了。
\(k=3\) 时就等同于前面 \(k\) 很大的情况啦。
然后我们就可以轻松切了这题啦。
code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int k;
int solve(int x1,int y1,int x2,int y2)
{
if(k==2) return 2*max(abs(x1-x2),abs(y1-y2))-abs(abs(x1-x2)-abs(y1-y2))/2;
return 2*max(abs(x1-x2),abs(y1-y2));
}
vector<pair<pair<int,int>,int>>v[2];
void check(int x,int y,int op)
{
if((x/k+y/k)%2) v[op].push_back({{x/k,y/k},0});
else
v[op].push_back({{x/k-1,y/k},(x%k)+1}),v[op].push_back({{x/k,y/k-1},(y%k)+1}),
v[op].push_back({{x/k+1,y/k},k-(x%k)}),v[op].push_back({{x/k,y/k+1},k-(y%k)});
}
signed main()
{
int x1,y1,x2,y2,ans=1e18;
cin>>k;
cin>>x1>>y1>>x2>>y2;
if(k==1) {cout<<abs(y1-y2)+abs(x1-x2);return 0;}
if(x1/k==x2/k&&y1/k==y2/k) ans=abs(y1-y2)+abs(x1-x2);
check(x1,y1,0);check(x2,y2,1);
for(auto i:v[0]) for(auto j:v[1]) ans=min(ans,solve(i.first.first,i.first.second,j.first.first,j.first.second)+i.second+j.second);
cout<<ans;
return 0;
}