拓扑排序
大家好,我是Weekoder!
接上次的二分查找,我又打算写一篇关于拓扑排序的文章!
本文涉及到的知识比较多,请确认已经掌握了以下知识:
其中,第二条并不是必要的,只要你能用自己的方法遍历图上任意一个点所有出边,如使用链式前向星。
好了,当你掌握了这些知识后,我们就可以进入主题了。
拓扑排序的理论概念
在有向无环图(DAG)中,将\(n\)个结点整理出一组排列,使得对于每一条边\(x\to y\),在排列中\(x\)总是在\(y\)之前,这样的排列称为原图的拓扑序,而制造出拓扑序的算法称为拓扑排序。
拓扑排序的作用
当我们做事情时,往往需要有一个先后顺序。就像早上你需要先起床,再洗脸刷牙,换衣服,然后吃早餐,最后出门。你总不能先出门再起床吧。我们把这些需要处理的事情看作图上的点,事情之间的关系看作一条有向边,这种先后顺序就是拓扑序。这只是一个简单的例子,但如果你有\(100\)个事情,\(1000\)个事情甚至\(10000\)个事情时,他们之间还得有一定的先后顺序,肯定是处理不过来的,于是就有了拓扑排序来处理这类问题。
而又因为洗脸刷牙和换衣服不分先后顺序,所以拓扑序不一定是唯一的。
提问/解释环节
- 有向无环图是啥?
由有向边组成的没有环的图叫有向无环图,又叫DAG。
- 没什么非得是有向无环图?
有向:
因为我们需要满足对于每一条边\(x\to y\),在排列中\(x\)总是在\(y\)之前,但是在无向图的无向边中是没有前后的概念的。
无环:
我们再来举个例子。假设有两个需要处理的事情\(x\)和\(y\),并且处理\(y\)需要在\(x\)之前,处理\(x\)需要在\(y\)之前。 这里肯定有人就会觉得奇怪,先别急,我们把它的图给画出来。
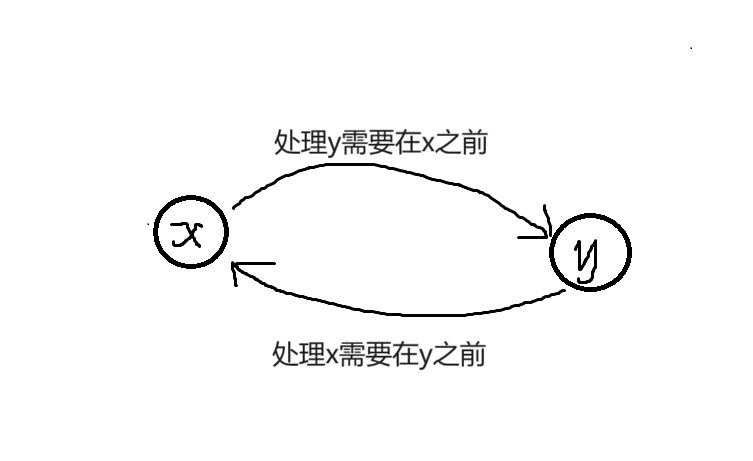
可以看到,一条\(x\to y\)的边代表处理\(y\)需要在\(x\)之前,而一条\(y\to x\)的边代表处理\(x\)需要在\(y\)之前。那这不是矛盾了吗? 没错,因为这样的信息导致既不能完成\(x\),也不能完成\(y\),同时还导致上面的图形成了一个环。 也就是说,图中有环会导致信息产生矛盾,从而无法完成所有的事件。
实现拓扑排序
题目大意:
给出\(n\)个人的后代,将\(n\)个人整理出一种顺序,使得辈分大的在前面,小的在后面。
分析:
既然是要整理出一种顺序,不妨试试拓扑排序。我们可以把每个人看作一个结点,并且因为要先输出辈分大的,所以将祖先指向后代来建造有向边。而且这里是一定不会出现环的,因为不可能出现我是你爸爸,然后你又是我爷爷之类的事情,因此只可能构造一个有向无环图。
代码:
先把我的代码贴上来,接下来我会跟着代码上的注释逐一讲解。
\(Code\):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5; // 数组大小
int n, in[N], x; // 分别是人数,每个点的入度,输入变量
vector<int> nbr[N]; // 存图
// 先去看主函数!
void topo() { // 封装成一个函数
queue<int> q; // 用队列进行操作
for (int i = 1; i <= n; i++) // 先将所有入度为0的点入队
if (!in[i]) // 判断入度是否为0
q.push(i); // 入队
while (!q.empty()) { // 当队列不为空时执行(还有入度为0的点)
int cur = q.front(); // 先记录即将要输出并且要遍历后代的点
q.pop(); // 删除入度为0的点
cout << cur << " "; // 先输出
for (auto nxt : nbr[cur]) { // 看不懂的可以改为:for (int nxt = 0; nxt < nbr[cur].size(); nxt++) 遍历这个点的所有后代
in[nxt]--; // 入度减1
if (!in[nxt]) // 如果入度为0
q.push(nxt); // 入队
}
}
return ; // 一定要写返回!回去看主函数
}
int main() {
ios::sync_with_stdio(0); // 这个可以不用管
cin >> n; // 输入人数
for (int i = 1; i <= n; i++) { // 循环读入每个人的后代
while (1) {
cin >> x; // 输入后代
if (!x) // 如果为0则跳出
break; // 跳出
nbr[i].emplace_back(x); // 记录i的后代
in[x]++; // x的入度加1
}
}
topo(); // 去看拓扑排序函数
return 0; // 大功告成!
}
OK,我们从主函数看起。
首先是一些输入,我就不讲解了,来看\(while\)循环里的倒数两句:
nbr[i].emplace_back(x);
in[x]++;
这两句是什么意思呢?首先,这里用到了一个\(vector\)容器\(nbr[N]\)和一个数组\(in\)。它们分别是用来干什么的呢?\(nbr[i]\)里面存的是\(i\)的后代,在图中可以理解为\(i\)指向的所有点。因为并不确定有多少个,所以使用\(STL\) \(vector\)。而\(in[i]\)代表的是点\(i\)的入度。点\(i\)的入度指的是有多少条边直接指向\(i\)。比如有三条边\(j\to i\),\(k\to i\),\(x\to j\),那么\(i\)的入度就是\(2\)。于是这里我们就往\(nbr[i]\)中加入了他的后代\(x\),并且因为在图中相当于是\(i\)指向了\(x\),于是\(x\)的入度就加了\(1\)。
接下来就该调用我们的拓扑排序函数\(topo\)啦!
在\(topo\)函数中我们需要用到队列的操作,\(STL\) \(queue\)或手写队列都可以。我这里用的是\(STL\) \(queue\)。我们来看看我们要怎样找到一个拓扑序。我们刚才说过\(i\)的入度指的是有多少条边直接指向\(i\),那么假设我们现在要在图中输出一个符合拓扑序的点\(i\),\(i\)应该符合什么条件呢?答案是入度为\(0\)。因为假设现在输出的\(i\)是一个入度大于\(0\)的点,那么就必定有一条边\(x\to i\)。也就是如果现在输出\(i\),那么\(x\)就在\(i\)之后了,不符合拓扑序的规则。
现在我们知道了我们要找入度为\(0\)的点输出,那么我们输出了以后当然也要删除它。于是它指向的所有点的入度都要减\(1\)。但当这些点减了\(1\)后,若它的入度变为\(0\),则也需要将它入队。请结合代码中的注释自行理解。
总结 + 挑战例题
拓扑排序就是一直将入度为零的点输出、删除并继续统计,最后得到拓扑序,并且这个算法的时间复杂度是\(O(n+m)\)。你是否理解了呢?这里我再给大家出一道挑战例题,相信你一定能\(AC\)。
洛谷\(P2712\) 摄像头