\(\color{black}\text{P2390 地标访问 (传送门)}\)
学过区间 DP 的,看到这题的第一反应都是:访问的地标一定是一个区间,并且在不断扩大,区间 DP!可看到数据范围,又瞬间放弃了。与 P1220 关路灯 不同,这题由于没有电量的消耗等额外因素,有这样一个小性质:
- 贝西的行走路线只可能是三种:一路向左,一路向右或者在中途折返一次。
一路向左和一路向右倒还好理解,可为什么最多只会折返一次呢?考虑以下情况:
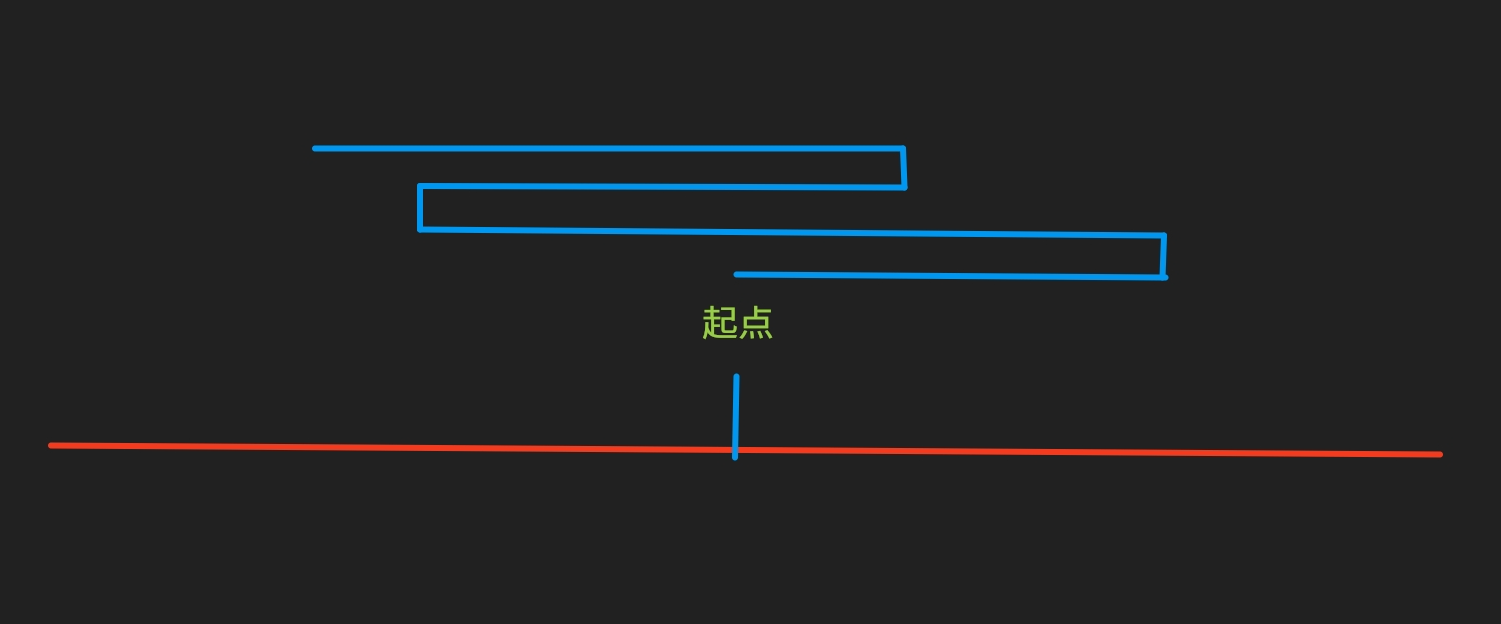
如图,贝西从起点出发,折返了多次以访问所有地标。可问题是,以下做法不仅能满足要求,也更优:
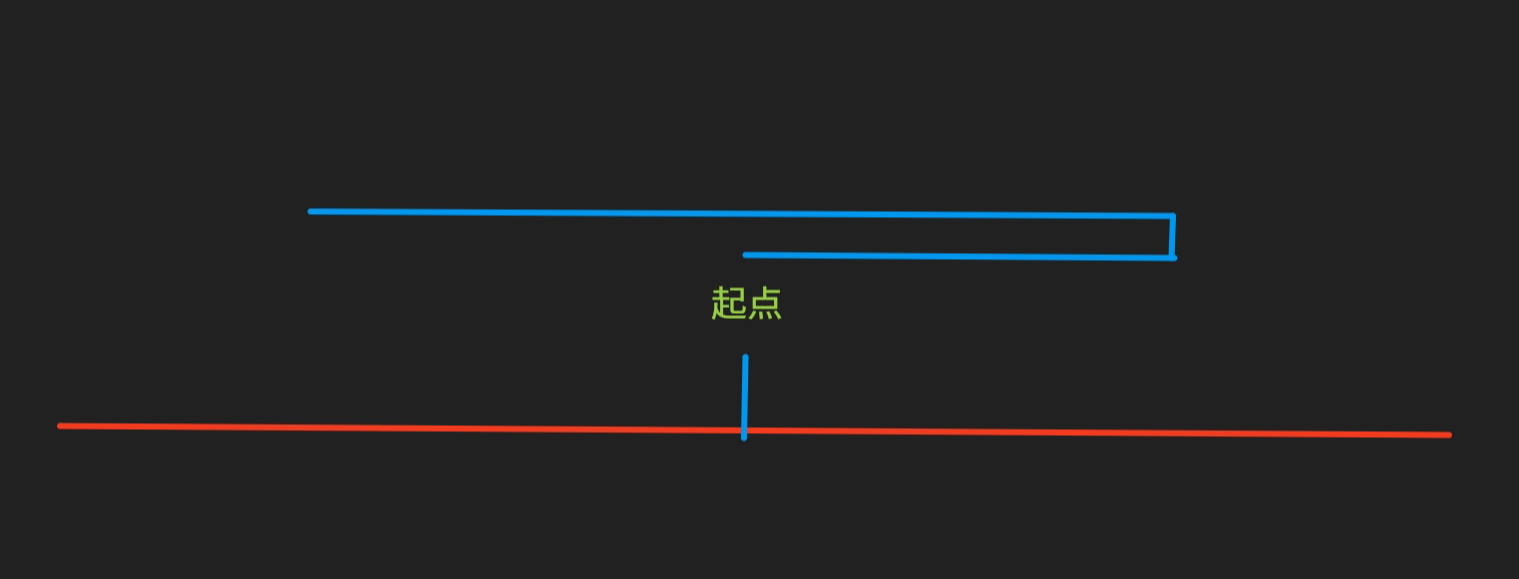
换句话说,由于我们访问的地标总是一个区间,而从某个点开始走完整个区间分为三种情况:
- 起点在区间左边,一路向右;
- 起点在区间右边,一路向左;
- 起点在区间里,先前往比较近的端点(左端点或者右端点),再前往另一个端点走完整个区间。
那么,现在问题来了:我们到底能走多少个地标呢?这取决于我们拥有的时间 \(t\)。换句话说,这是在满足条件(所用时间 \(\bm{\le t}\))的情况下找最值。这不就是一个二分答案吗?而且单调性也是显然的:如果不能访问 \(x\) 个地标,那也访问不了 \(y(y>x)\) 个地标;如果能访问 \(x\) 个地标,那也访问的了 \(y(y<x)\) 个地标。
考虑二分答案。难点在于,如何设计 \(\text{check}\) 函数?假设当前二分答案猜测可以访问 \(X\) 个地标,则需要选择连续的 \(X\) 个地标(地标已经按坐标大小排序),即 \(x_1,x_2,\dots,x_X\) 或者 \(x_2,x_3,\dots,x_{X+1}\) 或者 \(x_3,x_4,\dots,x_{X+2}\ \dots\) 我们可以枚举这些区间的终点 \(i\in[X,n]\),则区间的起点为 \(st=i-X+1\)。考虑上面的三种情况:一路向右,一路向左,起点在区间里,只要有一个满足条件就返回 \(\text{True}\)。条件判断的表达式分别为:
x[st] >= 0 && x[i] <= t
x[i] <= 0 && abs(x[st]) <= t
x[st] <= 0 && x[i] >= 0 && min(abs(x[st]), x[i]) + x[i] - x[st] <= t
完全再现了上面的三种情况。
如此一来,代码也就非常好写了:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e4 + 5;
int t, n, a[N];
bool check(int X) {
for (int i = X; i <= n; i++) {
int st = i - X + 1;
if (a[st] >= 0 && a[i] <= t)
return 1;
else if (a[i] <= 0 && abs(a[st]) <= t)
return 1;
else if (a[st] <= 0 && a[i] >= 0 && min(abs(a[st]), a[i]) + a[i] - a[st] <= t)
return 1;
}
return 0;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> t >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
sort(a + 1, a + 1 + n);
int l = -1, r = 5e4 + 1;
while (l + 1 < r) {
int mid = l + r >> 1;
if (check(mid))
l = mid;
else
r = mid;
}
cout << l;
return 0;
}