首页 > 其他分享 >Codeforces Round 950 (Div. 3)个人题解(A~F1)

Codeforces Round 950 (Div. 3)个人题解(A~F1)

时间：2024-06-04 22:16:30浏览次数：22  
标签：10 typedef F1 int 题解 ++ 测试用例 950 YES

Codeforces Round 950 (Div. 3)个人题解(A~F1)

题解火车头

#define _CRT_SECURE_NO_WARNINGS 1

#include <iostream>
#include <vector>
#include <algorithm>
#include <set>
#include <unordered_map>
#include <cstring>
#include <cstdio>
#include <string>
#include <queue>
#include <stack>
#include <map>
#include <list>
#include <bitset>
#include <cmath>
#include <numeric>

#define endl '\n'

#define ft first
#define sd second

#define yes cout << "yes\n"
#define no cout << "no\n"

#define Yes cout << "Yes\n"
#define No cout << "No\n"

#define YES cout << "YES\n"
#define NO cout << "NO\n"

#define pb push_back
#define eb emplace_back

#define all(x) x.begin(), x.end()
#define unq_all(x) x.erase(unique(all(x)), x.end())
#define sort_all(x) sort(all(x))
#define reverse_all(x) reverse(all(x))

#define INF 0x7fffffff
#define INFLL 0x7fffffffffffffffLL

#define RED cout << "\033[91m"
#define GREEN cout << "\033[92m"
#define YELLOW cout << "\033[93m"
#define BLUE cout << "\033[94m"
#define MAGENTA cout << "\033[95m"
#define CYAN cout << "\033[96m"
#define RESET cout << "\033[0m"

// 红色
#define DEBUG1(x)                     \
    RED;                              \
    cout << #x << " : " << x << endl; \
    RESET;

// 绿色
#define DEBUG2(x)                     \
    GREEN;                            \
    cout << #x << " : " << x << endl; \
    RESET;

// 蓝色
#define DEBUG3(x)                     \
    BLUE;                             \
    cout << #x << " : " << x << endl; \
    RESET;

// 品红
#define DEBUG4(x)                     \
    MAGENTA;                          \
    cout << #x << " : " << x << endl; \
    RESET;

// 青色
#define DEBUG5(x)                     \
    CYAN;                             \
    cout << #x << " : " << x << endl; \
    RESET;

// 黄色
#define DEBUG6(x)                     \
    YELLOW;                           \
    cout << #x << " : " << x << endl; \
    RESET;

using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef long double ld;

typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<ld, ld> pdd;
typedef pair<string, string> pss;
typedef pair<string, int> psi;
typedef pair<string, ll> psl;

typedef vector<bool> vb;
typedef vector<int> vi;
typedef vector<ll> vl;
typedef vector<string> vs;
typedef vector<pii> vpii;
typedef vector<pll> vpll;
typedef vector<pss> vpss;

typedef vector<vi> vvi;
typedef vector<vl> vvl;

typedef queue<int> qi;
typedef queue<ll> ql;
typedef queue<pii> qpii;
typedef queue<pll> qpll;
typedef queue<psi> qpsi;
typedef queue<psl> qpsl;

typedef priority_queue<int> pqi;
typedef priority_queue<ll> pql;
typedef priority_queue<string> pqs;
typedef priority_queue<pii> pqpii;
typedef priority_queue<psi> pqpsi;
typedef priority_queue<pll> pqpl;
typedef priority_queue<psi> pqpsl;

typedef map<int, int> mii;
typedef map<int, bool> mib;
typedef map<ll, ll> mll;
typedef map<ll, bool> mlb;
typedef map<char, int> mci;
typedef map<char, ll> mcl;
typedef map<char, bool> mcb;
typedef map<string, int> msi;
typedef map<string, ll> msl;
typedef map<int, bool> mib;

typedef unordered_map<int, int> umii;
typedef unordered_map<ll, ll> uml;
typedef unordered_map<char, int> umci;
typedef unordered_map<char, ll> umcl;
typedef unordered_map<string, int> umsi;
typedef unordered_map<string, ll> umsl;

template <typename T>
inline void read(T &x)
{
    T f = 1;
    x = 0;
    char ch = getchar();
    while (0 == isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (0 != isdigit(ch))
        x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
    x *= f;
}

template <typename T>
inline void write(T x)
{
    if (x < 0)
    {
        x = ~(x - 1);
        putchar('-');
    }
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}

A. Problem Generator

题意

A. 问题生成器
每个测试的时间限制：1秒
每个测试的内存限制：256兆字节
输入：标准输入
输出：标准输出

弗拉德计划在下个月举行 m 轮比赛。每轮比赛应包含一个难度为 "A"、"B"、"C"、"D"、"E"、"F" 和 "G" 的问题。

弗拉德已经有了一个 n 个问题的题库，其中第 i 个问题的难度等级为 ai。题库中的问题可能不够，所以他可能需要再想出一些问题。

弗拉德想要尽可能少地提出问题，所以他要求你找出他需要提出的问题的最小数量，以便举行 m 轮比赛。

例如，如果 m=1，n=10，a='BGECDCBDED'，那么他需要想出两道题：一道难度为 "A"，一道难度为 "F"。

输入

第一行包含一个整数 t（1≤t≤1000）——测试用例的数量。

每个测试用例的第一行包含两个整数 n 和 m（1≤n≤50，1≤m≤5）——题库中的问题数量和即将举行的轮数。

每个测试用例的第二行包含一个长度为 n 的字符串 a，字符串中的字符从 'A' 到 'G'，表示题库中问题的难度。

输出

对于每个测试用例，输出一个整数——为了举行 m 轮比赛，需要提出的最小问题数量。

示例

输入

3
10 1
BGECDCBDED
10 2
BGECDCBDED
9 1
BBCDEFFGG

输出

2
5
1

解题思路

对于每个字母，如果不足\(m\)，就加入最终答案

题解

void solve()
{
    int n, m;
    cin >> n >> m;
    string s;
    cin >> s;
    ll ans = 0;
    vi mp(7);
    for (auto c : s)
    {
        mp[c - 'A']++;
    }
    for (auto i : mp)
    {
        ans += max(0, m - i);
    }
    cout << ans << endl;
}

B. Choosing Cubes

题意

B. 选择立方体
每个测试的时间限制：1秒
每个测试的内存限制：256兆字节
输入：标准输入
输出：标准输出

德米特里有 n 个立方体，从左到右编号为 1 到 n。索引为 f 的立方体是他的最爱。

德米特里把所有的立方体都扔到了桌子上，第 i 个立方体显示了数值 ai（1≤ai≤100）。之后，他按照数值从大到小的非递增顺序排列这些立方体。如果两个立方体显示的数值相同，它们可以按照任何顺序排列。

排序后，德米特里取出了前 k 个立方体。然后，他开始关注自己是否取出了最喜欢的立方体（注意，排序后立方体的位置可能会发生变化）。

例如，如果 n=5，f=2，a=[4,3,3,2,3]（最喜欢的立方体用绿色标出），k=2，可能会发生以下情况：

  • 在对 a=[4,3,3,3,2] 进行排序后，由于最喜欢的立方体排在了第二位，因此它将被移除。
  • 在对 a=[4,3,3,3,2] 进行排序后，由于最喜爱的立方体排在了第三位，因此它不会被移除。

输入

第一行包含一个整数 t（1≤t≤1000）——测试用例的数量。然后是测试用例的说明。

每个测试用例描述的第一行分别包含三个整数 n、f 和 k（1≤f,k≤n≤100）——立方体的数量、德米特里最喜欢的立方体的索引以及移除的立方体的数量。

每个测试用例描述的第二行包含 n 个整数 ai（1≤ai≤100）——立方体上显示的值。

输出

对于每个测试用例，输出一行——如果立方体在所有情况下都会被移除，则输出 "YES"；如果在任何情况下都不会被移除，则输出 "NO"；如果可能会被移除或留下，则输出 "MAYBE"。

您可以输出任何情况下的答案。例如，"YES"、"nO"、"mAyBe" 等字符串都可以作为答案。

示例

输入

12
5 2 2
4 3 3 2 3
5 5 3
4 2 1 3 5
5 5 2
5 2 4 1 3
5 5 5
1 2 5 4 3
5 5 4
3 1 2 4 5
5 5 5
4 3 2 1 5
6 5 3
1 2 3 1 2 3
10 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1
42
5 2 3
2 2 1 1 2
2 1 1
2 1
5 3 1
3 3 2 3 2

输出

MAYBE
YES
NO
YES
YES
YES
MAYBE
MAYBE
YES
YES
YES
NO

解题思路

我们只需要检查排完序之后比较在 $ k $ 位置的立方体\(a_k\)与最喜欢的立方体\(a_f\)的大小即可，如果\(a_k>a_f\)，说明\(a_f\)的位置在\(k\)之前，一定会被删；如果\(a_k<a_f\)，说明\(a_f\)的位置在\(k\)之后，一定不会被删；如果\(a_k=a_f\)，检查\(a_{k+1}\)，如果\(a_{k+1}=a_f\)，则有可能被删，否则一定被删。

题解

void solve()
{
    int n, f, k;
    cin >> n >> f >> k;
    vi a(n + 1);
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
    }
    int fa = a[f];
    sort(a.begin() + 1, a.end(), greater<int>());
    if (k == n)
        YES;
    else if (fa > a[k])
        YES;
    else if (fa < a[k])
        NO;
    else
    {
        if (a[k + 1] == fa)
            cout << "MAYBE" << endl;
        else
            YES;
    }
}

C. Sofia and the Lost Operations

题意

C. 索菲亚和失落的操作
每个测试的时间限制：2秒
每个测试的内存限制：256兆字节
输入：标准输入
输出：标准输出

索菲亚有一个由 n 个整数 a1, a2, ..., an 组成的数组。有一天，她对这个数组感到厌倦，于是决定依次对它进行 m 次修改操作。

每个修改操作都由一对数字 ⟨cj, dj⟩ 来描述，这意味着数组中索引为 cj 的元素应赋值为 dj，即执行赋值 acj=dj。在依次执行所有修改操作后，索菲亚丢弃了得到的数组。

最近，你发现了一个由 n 个整数组成的数组 b1, b2, ..., bn。你想知道这个数组是否是索菲亚的数组。你知道原始数组的值以及 d1, d2, ..., dm 的值。结果发现数值 c1, c2, ..., cm 丢失了。

是否存在一个序列 c1, c2, ..., cm 使得对数组 a1, a2, ..., an 的修改操作 ⟨c1, d1⟩, ⟨c2, d2⟩, ..., ⟨cm, dm⟩ 的顺序应用可以将其转换为数组 b1, b2, ..., bn 呢？

输入

第一行包含一个整数 t（1≤t≤104）——测试用例的数量。

然后是测试用例的说明。

每个测试用例的第一行都包含一个整数 n（1≤n≤2⋅105）——数组的大小。

每个测试用例的第二行包含 n 个整数 a1, a2, ..., an（1≤ai≤109）——原始数组的元素。

每个测试用例的第三行包含 n 个整数 b1, b2, ..., bn（1≤bi≤109）——找到的数组的元素。

第四行包含一个整数 m（1≤m≤2⋅105）——修改操作的次数。

第五行包含 m 个整数 d1, d2, ..., dm（1≤dj≤109）——每次修改操作的保留值。

保证所有测试用例中 n 的值之和不超过 2⋅105，同样，所有测试用例中 m 的值之和不超过 2⋅105。

输出

输出 t 行，每一行都是相应测试用例的答案。如果存在合适的序列 c1, c2, ..., cm，则输出 "YES"，否则输出 "NO"。

您可以在任何情况下输出答案（例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 将被识别为肯定答案）。

示例

输入

7
3
1 2 1
1 3 2
4
1 3 1 2
4
1 2 3 5
2 1 3 5
2
2 3
5
7 6 1 10 10
3 6 1 11 11
3
4 3 11
4
3 1 7 8
2 2 7 10
5
10 3 2 2 1
5
5 7 1 7 9
4 10 1 2 9
8
1 1 9 8 7 2 10 4
4
1000000000 203 203 203
203 1000000000 203 1000000000
2
203 1000000000
1
1
1
5
1 3 4 5 1

输出

YES
NO
NO
NO
YES
NO
YES

解题思路

检查\(a\)和\(b\)在同一位置不同值的每一个\(b_i\)是否都存在与\(d\)中。

注：\(d\)中最后一个位置的值一定要是\(b\)的任意一个值。

题解

void solve()
{
    int n;
    cin >> n;
    vi a(n);
    vi b(n);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    for (int i = 0; i < n; i++)
    {
        cin >> b[i];
    }
    int m;
    cin >> m;
    vi d(m);
    mii mp;
    for (int i = 0; i < m; i++)
    {
        cin >> d[i];
        mp[d[i]]++;
    }
    bool flag1 = true;
    bool flag2 = false;
    for (int i = 0; i < n; i++)
    {
        if (b[i] == d[m - 1])
            flag2 = true;
        if (a[i] != b[i])
        {
            if (mp[b[i]])
                mp[b[i]]--;
            else
                flag1 = false;
        }
    }
    if (flag1 && flag2)
        YES;
    else
        NO;
}

D. GCD-sequence

恶心的大模拟

题意

D. GCD序列
每个测试的时间限制：2秒
每个测试的内存限制：256兆字节
输入：标准输入
输出：标准输出

两个整数 x 和 y 的 GCD（最大公约数）是 z，可以整除 x 和 y 的最大整数。例如，GCD(36,48)=12，GCD(5,10)=5 和 GCD(7,11)=1。

克里斯蒂娜有一个由 n 个正整数组成的数组 a。她想通过计算每一对相邻数字的 GCD 得到一个新数组 b，称为 GCD 序列。

因此，GCD 序列 b 中的元素将使用公式 bi=GCD(ai,ai+1) 计算，1≤i≤n−1。

确定是否有可能从数组 a 中删除恰好一个数字，从而使 GCD 序列 b 不递减（即 bi≤bi+1 始终为真）。

例如，假设克里斯蒂娜有一个数组 a = [20,6,12,3,48,36]。如果她从中删除 a4=3，并计算 b 的 GCD 序列，她会得到：

  • b1=GCD(20,6)=2
  • b2=GCD(6,12)=6
  • b3=GCD(12,48)=12
  • b4=GCD(48,36)=12

得到的 GCD 序列 b = [2,6,12,12] 是不递减的，因为 b1≤b2≤b3≤b4。

输入

第一行输入数据包含一个数字 t (1≤t≤10^4) - 测试用例的数量。

随后是测试用例的描述。

每个测试用例的第一行包含一个整数 n (3≤n≤2⋅10^5) - 数组 a 中的元素个数。

每个测试用例的第二行包含 n 个整数 ai (1≤ai≤10^9) - 数组 a 中的元素。

保证所有测试用例中 n 的总和不超过 2⋅10^5。

输出

为每个测试用例输出一行：

  • 如果能从数组 a 中删除一个数字，使 b 的 GCD 序列不递减，则输出 "YES"；
  • 否则输出 "NO"。

您可以在任何情况下输出答案（例如，字符串 "yEs"、"yes"、"Yes" 和 "YES" 都会被识别为肯定答案）。

示例

输入

12
6
20 6 12 3 48 36
4
12 6 3 4
3
10 12 3
5
32 16 8 4 2
5
100 50 2 10 20
4
2 4 8 1
10
7 4 6 2 4 5 1 4 2 8
7
5 9 6 8 5 9 2
6
11 14 8 12 9 3
9
5 7 3 10 6 3 12 6 3
3
4 2 4
8
1 6 11 12 6 12 3 6

输出

YES
NO
YES
NO
YES
YES
NO
YES
YES
YES
YES
YES

解题思路

预处理出\(b\)中的递减序列，然后枚举每一个位置，检查一下这些递减序列是否变成非递减的就行

题解

void solve()
{
    int n;
    cin >> n;
    vi a(n);
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
    }
    if (n == 3)
    {
        YES;
        return;
    }
    vi b;
    for (int i = 0; i < n - 1; i++)
    {
        b.pb(__gcd(a[i], a[i + 1]));
    }
    mii wrong;
    for (int i = 0; i < n - 2; i++)
    {
        if (b[i] > b[i + 1])
            wrong[i]++;
    }
    if (wrong.size() == 0)
    {
        YES;
        return;
    }
    bool flag = false;
    for (int i = 0; i < n; i++)
    {
        if (i == 0)
        {
            if (b[i] > b[i + 1] && (int)wrong.size() == 1)
                flag = true;
        }
        else if (i == n - 1)
        {
            if (b[i - 2] > b[i - 1] && (int)wrong.size() == 1)
                flag = true;
        }
        else
        {
            int loss = __gcd(a[i - 1], a[i + 1]);
            if (i - 2 >= 0 && loss < b[i - 2])
                continue;
            if (i + 1 < n - 1 && b[i + 1] < loss)
                continue;
            int len = 0;
            if (i - 2 >= 0 && b[i - 2] > b[i - 1])
                len++;
            if (i <= n - 2 && b[i - 1] > b[i])
                len++;
            if (i + 1 <= n - 2 && b[i] > b[i + 1])
                len++;
            if (wrong.size() - len == 0)
                flag = true;
        }
    }
    if (flag)
        YES;
    else
        NO;
}

E. Permutation of Rows and Columns

题意

E. 行和列的排列

题目描述

给你一个大小为 n 乘 m 的矩阵 a，其中包含从 1 到 n⋅m 的整数排列。

一个由 n 个整数组成的排列是一个数组，其中包含了从 1 到 n 的所有整数。例如，数组 [1]、[2,1,3]、[5,4,3,2,1] 是排列，而数组 [1,1]、[100]、[1,2,4,5] 不是排列。

如果一个矩阵的所有元素都写出后，得到的数组是一个排列，那么这个矩阵就包含一个排列。矩阵 [[1,2],[3,4]]、[[1]]、[[1,5,3],[2,6,4]] 包含排列，而矩阵 [[2]]、[[1,1],[2,2]]、[[1,2],[100,200]] 不包含排列。

您可以在一次操作中执行以下两个操作之一：

  1. 选择列 c 和 d (1≤c,d≤m, c≠d) 并交换这些列；
  2. 选择行 c 和 d (1≤c,d≤n, c≠d) 并交换这些行。

您可以执行任意数量的操作。

给你原始矩阵 a 和矩阵 b。您的任务是确定是否有可能通过给定的运算将矩阵 a 变换成矩阵 b。

输入

第一行包含一个整数 t (1≤t≤10^4) - 测试用例的数量。下面是测试用例的说明。

每个测试用例描述的第一行包含 2 个整数 n 和 m (1≤n,m≤n⋅m≤2⋅10^5) - 矩阵的大小。

接下来的 n 行分别包含 m 个整数 aij (1≤aij≤n⋅m)。可以保证矩阵 a 是一个排列。

接下来的 n 行分别包含 m 个整数 bij (1≤bij≤n⋅m)。可以保证矩阵 b 是一个排列。

保证所有测试用例的值 n⋅m 之和不超过 2⋅10^5。

输出

对于每个测试用例，如果可以从第一个矩阵得到第二个矩阵，则输出 "YES"，否则输出 "NO"。

您可以以任何大小写(小写或大写)输出每个字母。例如，字符串 "yEs"、"yes"、"Yes "和 "YES "将被视为肯定答案。

示例

输入

7
1 1
1
1
2 2
1 2
3 4
4 3
2 1
2 2
1 2
3 4
4 3
1 2
3 4
1 5 9 6
12 10 4 8
7 11 3 2
1 5 9 6
12 10 4 8
7 11 3 2
3 3
1 5 9
6 4 2
3 8 7
9 5 1
2 4 6
7 8 3
2 3
1 2 6
5 4 3
6 1 2
3 4 5
1 5
5 1 2 3 4
4 2 5 1 3

输出

YES
YES
NO
YES
YES
NO
YES

注

在第二个例子中，原始矩阵如下所示：

1 3
2 4

交换行 1 和 2 后，矩阵变为：

3 1
4 2

交换 1 和 2 列后，它就等于矩阵 b：

4 2
3 1

解题思路

很容易就可以观察到，无论怎么进行交换，每一行拥有的数字都不会变，只是位置改变了，对于每一列同样也是如此。所以只需要逐行和逐列的去检查\(b\)矩阵的一行或一列对应的数字集合是否在\(a\)中出现即可。

题解

void solve()
{
    int n, m;
    cin >> n >> m;
    vector<vi> a(n, vi(m));
    vector<vi> b(n, vi(m));
    map<vi, int> mp_col;
    for (int i = 0; i < n; i++)
    {
        vi temp;
        for (int j = 0; j < m; j++)
        {
            cin >> a[i][j];
            temp.eb(a[i][j]);
        }
        sort_all(temp);
        mp_col[temp]++;
    }
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < m; j++)
        {
            cin >> b[i][j];
        }
    }
    for (int i = 0; i < n; i++)
    {

        vi temp;
        for (int j = 0; j < m; j++)
        {
            temp.eb(b[i][j]);
        }
        sort_all(temp);
        if (mp_col[temp] == 0)
        {
            NO;
            return;
        }
    }
    map<vi, int> mp_row;
    for (int j = 0; j < m; j++)
    {
        vi temp;
        for (int i = 0; i < n; i++)
        {
            temp.eb(a[i][j]);
        }
        sort_all(temp);
        mp_row[temp]++;
    }
    for (int j = 0; j < m; j++)
    {
        vi temp;
        for (int i = 0; i < n; i++)
        {
            temp.eb(b[i][j]);
        }
        sort_all(temp);
        if (mp_row[temp] == 0)
        {
            NO;
            return;
        }
    }
    YES;
}

F1. Field Division (easy version)

题意

Alice 和 Bob 正在分割田地。田地是一个大小为 n×m（2≤n,m≤10^9）的矩形，行从上到下编号为 1 到 n，列从左到右编号为 1 到 m。行和列的交叉处的单元格用 (r,c) 表示。

Bob 有 k（2≤k≤2⋅10^5）个喷泉，它们都位于田地的不同单元格中。Alice 负责分割田地，但她必须满足几个条件：

  • 要分割田地，Alice 将从田地左侧或上侧的任意空闲（无喷泉）单元格开始移动，每次移动都会移动到相邻的下或右单元格。她的路径将在场地的右侧或底侧结束。
  • Alice 的路径将区域分为两部分 — 一部分将属于 Alice（这部分包括她路径上的单元格），另一部分将属于 Bob。
  • Alice 将拥有包含单元格 (n,1) 的部分。
  • Bob 将拥有包含单元格 (1,m) 的部分。

Alice 希望以这样一种方式分割田地，以获得尽可能多的单元格。

Bob 希望保留所有喷泉的所有权，但他可以将其中一个喷泉交给 Alice。首先，输出整数 α — 如果 Bob 不给 Alice 任何喷泉（即所有喷泉都保留在 Bob 的地块上），Alice 可以拥有的地块的最大面积。然后输出 k 个非负整数 a1,a2,…,ak，其中：

  • ai=0，如果 Bob 给了 Alice 第 i 个喷泉后，与所有 k 个喷泉都属于 Bob 的情况相比，Alice 的地块的最大可能大小没有增加；
  • ai=1，如果 Bob 给了 Alice 第 i 个喷泉，那么与所有 k 个喷泉都属于 Bob 的情况相比，Alice 的地块的最大可能大小会增加。

输入

第一行包含一个整数 t（1≤t≤10^4） - 测试用例数。

每个测试用例的第一行包含三个整数 n、m 和 k（2≤n,m≤10^9, 2≤k≤2⋅10^5）-- 字段大小和喷泉数量。

接下来是 k 行，每行包含两个数字 ri 和 ci（1≤ri≤n, 1≤ci≤m）-- 即带有第 i 个喷泉的单元格的坐标。保证所有单元格都是不同的，没有一个单元格是 (n,1)。

保证所有测试用例的 k 之和不超过 2⋅10^5。

输出

对于每个测试案例，首先输出 α - 如果 Bob 不给 Alice 任何喷泉，Alice 可以拥有的地块的最大面积。然后输出 k 个非负整数 a1,a2,…,ak，其中：

  • ai=0，如果 Bob 给了 Alice 第 i 个喷泉后，与所有 k 个喷泉都属于 Bob 的情况相比，Alice 的地块的最大可能大小没有增加；
  • ai=1，如果 Bob 给了 Alice 第 i 个喷泉，那么与所有 k 个喷泉都属于 Bob 的情况相比，Alice 的地块的最大可能大小会增加。

如果你输出任何其他适合 64 位有符号整数类型的正数代替 1，它也会被识别为 1。因此，这个问题的难解版本也能通过简单版本的测试。

示例

输入

5
2 2 3
1 1
1 2
2 2
5 5 4
1 2
2 2
3 4
4 3
2 5 9
1 2
1 5
1 1
2 2
2 4
2 5
1 4
2 3
1 3
6 4 4
6 2
1 3
1 4
1 2
3 4 5
2 1
3 2
1 4
1 3
2 4

输出

1
1 0 1 
11
0 1 0 1 
1
0 0 1 1 0 0 0 0 0 
6
1 0 0 0 
1
1 1 0 0 0

注

以下是第二个示例的图片：

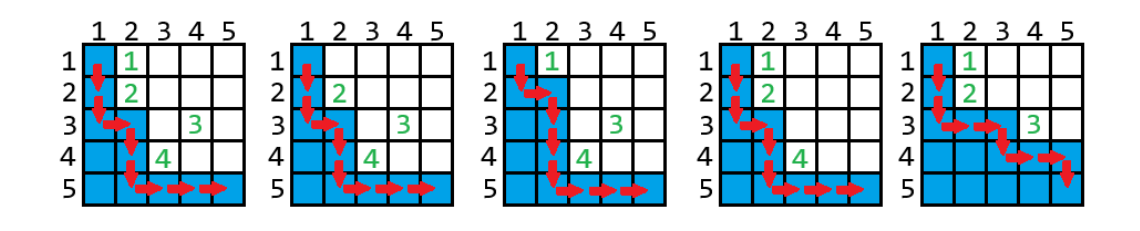
image-20240604023914297

喷泉的指数用绿色标出。属于 Alice 的单元格用蓝色标出。

请注意，如果 Bob 给了 Alice 喷泉 1 或喷泉 3，那么该喷泉就不可能出现在 Alice 的地块上。

解题思路

我们只需要对喷泉按行坐标排个序，然后进行枚举即可，枚举的时候要维护一下上限。

题解

struct fountain
{
    ll x, y, idx;
};
bool cmp(fountain a, fountain b)
{
    if (a.x != b.x)
        return a.x < b.x;
    return a.y < b.y;
};
void solve()
{
    ll n, m, k;
    cin >> n >> m >> k;
    vl x(k + 1);
    vl y(k + 1);
    for (int i = 1; i <= k; i++)
    {
        cin >> x[i] >> y[i];
    }
    vector<fountain> founs;
    for (int i = 1; i <= k; i++)
    {
        founs.pb({n - x[i] + 1, y[i], i});
    }
    sort(all(founs), cmp);
    vpll temp;
    ll mn = INFLL;
    ll ans = 0;
    for (int i = 0; i < k; i++)
    {
        bool flag = false;
        if (i == 0)
            flag = true;
        else if (founs[i].y < mn)
            flag = true;
        if (flag)
        {
            temp.pb({x[founs[i].idx], founs[i].y});
            x[founs[i].idx] = 1;
            mn = founs[i].y;
        }
        else
            x[founs[i].idx] = 0;
    }
    if (temp[0].ft != n)
        ans += (n - temp[0].ft) * m;
    temp.pb({0, 0});
    for (int i = 0; i < temp.size() - 1; ++i)
    {
        ans += (temp[i].ft - temp[i + 1].ft) * (temp[i].sd - 1);
    }
    cout << ans << endl;
    for (int i = 1; i <= k; i++)
    {
        cout << x[i] << ' ';
    }
    cout << endl;
}

标签：10,typedef,F1,int,题解,++,测试用例,950,YES
From： https://www.cnblogs.com/extractstars/p/18231860

相关文章

  • 按按钮题解
    按按钮题解在量体温，打不了代码，来写题解。赞美lwq，三句话让我跟上了课堂节奏。题意数轴\(n\)个按钮，第\(i\)个按钮在坐标\(i\)。有\(m\)次询问，\(i\)询问为在时刻\(t_i\)按下\(b_i\)。可以在时刻\(0\)安排一些机器人，机器人可以花\(1\)单位时间向左或右移动\(1\)......
  • acwing329 围栏障碍训练场 题解
    考试压轴题，意识到这题是线段树优化\(dp\)时追悔莫及。为了简化题目，我将从起点到原点变成了从原点到起点（这样就可以省去两个数组的空间）。想到设\(dp_{i,j}\)表示在第\(i\)层，奶牛们在\(j\)列时的最小移动范围，则转移方程为（设输入为\(l,r\)）:\[\begin{cases}dp_{i,j}=dp_{......
  • CF1572A Book
    题目链接:https://codeforces.com/problemset/problem/1572/A大致思路:题目想问的是从头到尾阅读多少次之后,才能读完这本书.这是一道很套路的拓扑排序的题.看到一个事件有前置条件这种,就应该想到建一个有向无环图然后跑拓扑排序,在这里,我们建立一条从前置条件指向当前页码的......
  • CF1980
    小号打的抽象比赛，谁知道再给我30min能不能AK？AB一眼。Cunordered_map会被卡，建议multiset。D前缀和后缀和。E发现列和行是独立的，于是对列和行分别检查。若置换矛盾，则不合法。F经过观察，一行的答案为后缀最小值-1。所以F1就能做出来了。考虑F2，对行拆贡献，维护后缀......
  • 会前会后系统Q&A：董事会管理工具相关问题解答
    不同企业在购买董事会管理工具时，都会带有不同的功能需求，希望能够借此提升本企业的董事会管理效率和质量。作为垂直领域的专业SaaS工具，会前会后针对董事会的工作流程研发，符合董事会成员的使用系统，在董事履职、董事会管理中提供颇多助力。下面是关于会前会后系统董事会管理工具......
  • Codeforces Round 949 (Div. 2) 中文题解
    A对于一个特定的\(x\)，Piggy总是会选择\(p\)使得\(p\)是质数，所以分数就是\(x\)的质因子个数。容易发现至少有\(t\)个质因子的数是\(2^t\)。最大的满足\(2^t\ler\)的整数\(t\)是\(\left\lfloor\log_2r\right\rfloor\)。又因为\(2l\ler\)，所以\(\log_2l+......
  • gpt4free软件的 g4f gui 网页速度非常慢的问题解决
    问题：g4f gui启动网页很难连上gpt4free是一个为大众提供的Openai等大模型API调用服务的软件，但是在装好启动g4f gui，使用8080端口连接后，发现网页一直在执行，半天还没好。怀疑是网页里面的一些js加载有问题。通过在python命令行使用importg4f;g4f.version命令来找到g4f的......
  • MySQL数据库：Lock wait timeout exceeded； try restarting transaction问题解析及解决方
    MySQL数据库：Lockwaittimeoutexceeded;tryrestartingtransaction问题解析及解决方案一、背景描述二、原因分析三、解决方案3.1方案一事务信息查询3.2方案二如果杀掉线程依然不能解决，可以查找执行线程耗时比较久的任务，kill掉3.3方案三innodb_lock_wait_timeout锁定等......
  • (第25天)【leetcode题解】二叉树的层序遍历
    目录429、N叉树的层序遍历题目描述思路代码515、在每个树行中找最大值题目描述思路代码116、填充每个节点的下一个右侧节点指针题目描述思路代码117、填充每个节点的下一个右侧节点指针II题目描述思路代码104、二叉树的最大深度题目描述思路代码111、二叉树的最小深......
  • 2009年408真题解析
    2009年408真题解析【2009.1】为解决计算机主机与打印机之间速度不匹配问题，通常设置一个打印数据缓冲区，主机将要输出的数据依次写入该缓冲区，而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是。A.栈B.队列C.树D.图【知识点】栈和队列特点及应用。【答案】B......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99